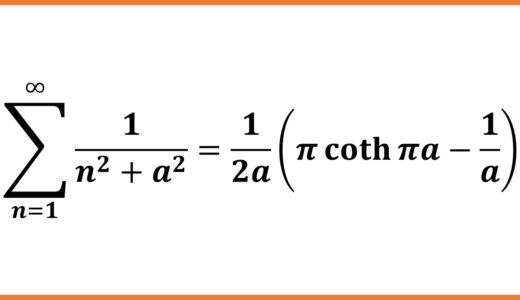\begin{equation}\sum_{n=1}^\infty\frac{(-1)^n}{n^2+1}\tag{1}\end{equation}\begin{equation}\sum_{n=1}^\infty\frac{(-1)^n}{n^2+a^2}\tag{2}\end{equation}
まず(1)を複素フーリエ級数を使って求め,その応用問題として(2)を取り上げます.
関数 $f(x)$ の $-\pi<x<\pi$ における複素フーリエ級数展開は$$f(x)=\sum^\infty_{n=-\infty}c_ne^{inx}$$ここでは正負別々に極限をとるのではなく,「同じスピードで」極限をとります.つまり $n=-N$ から $N$ までとして,$N$ を無限大にします.$$\displaystyle\lim_{N\to\infty}\sum^N_{n=-N}c_ne^{inx}$$
さて今回の級数にあたっては$$e^x=\sum^\infty_{n=-\infty}c_ne^{inx}$$を考えます.両辺に $e^{-imx}$ をかけて積分すると$$\int_{-\pi}^\pi e^xe^{-imx}dx=\sum^\infty_{n=-\infty}c_n\int_{-\pi}^\pi e^{inx}e^{-imx}dx$$$$\therefore\;\frac{(-1)^m(e^\pi-e^{-\pi})}{1-im}=\sum^\infty_{n=-\infty}c_n\int_{-\pi}^\pi e^{i(n-m)x}dx$$右辺の積分は $n\neq m$ では $0$ となるので結局$$\frac{(-1)^m(e^\pi-e^{-\pi})}{1-im}=c_m\int_{-\pi}^\pi dx$$計算を進めると\begin{eqnarray*}c_m&=&\frac{(-1)^m(e^\pi-e^{-\pi})}{2\pi(1-im)}\\&=&\frac{\sinh\pi}{\pi}\frac{(-1)^m(1+im)}{m^2+1}\end{eqnarray*}以上より $e^x$ の複素フーリエ級数表示は$$e^x=\frac{\sinh\pi}{\pi}\sum^\infty_{n=-\infty}\frac{(-1)^n(1+in)}{n^2+1}e^{inx}\;\;(-\pi<x<\pi)$$となりました.邪魔者はありますが,求めたい無限級数の形が見えています.
これに $x=0$ を代入すると$$1=\frac{\sinh\pi}{\pi}\sum^\infty_{n=-\infty}\frac{(-1)^n(1+in)}{n^2+1}$$変形してから,総和の範囲を負,正,0に分けて考えると虚部が消えて,すっきりまとまります.\begin{eqnarray*}\frac{\pi}{\sinh\pi}&=&\sum^\infty_{n=-\infty}\frac{(-1)^n(1+in)}{n^2+1}\\&=&\sum^\infty_{n=-\infty}\frac{(-1)^n}{n^2+1}+i\sum^\infty_{n=-\infty}\frac{(-1)^nn}{n^2+1}\\&=&2\sum^\infty_{n=1}\frac{(-1)^n}{n^2+1}+1\end{eqnarray*}以上から
\begin{equation}\;\sum_{n=1}^\infty\frac{(-1)^n}{n^2+1}=\frac{1}{2}\left(\frac{\pi}{\sinh\pi}-1\right)\tag{3}\end{equation}
$e^{ax}$ を複素フーリエ展開し\begin{equation}\sum_{n=1}^\infty\frac{(-1)^n}{n^2+a^2}\tag{2}\end{equation}を求めよ.
$$e^{ax}=\sum^\infty_{n=-\infty}c_ne^{inx}$$とおきます.両辺に $e^{-imx}$ をかけて積分すると$$\int_{-\pi}^\pi e^{(a-im)x}dx=\sum^\infty_{n=-\infty}c_n\int_{-\pi}^\pi e^{inx}e^{-imx}dx$$$$\therefore\;\frac{(-1)^m(e^{a\pi}-e^{-a\pi})}{a-im}=\sum^\infty_{n=-\infty}c_n\int_{-\pi}^\pi e^{i(n-m)x}dx$$右辺の積分は $n\neq m$ で $0$ となるので$$\frac{(-1)^m(e^{a\pi}-e^{-a\pi})}{a-im}=2\pi c_m$$計算を進めると\begin{eqnarray*}c_m&=&\frac{(-1)^m(e^{a\pi}-e^{-a\pi})}{2\pi(a-im)}\\&=&\frac{\sinh a\pi}{\pi}\frac{(-1)^m(a+im)}{m^2+a^2}\end{eqnarray*}以上より $e^{ax}$ の複素フーリエ級数表示は$$e^{ax}=\frac{\sinh a\pi}{\pi}\sum^\infty_{n=-\infty}\frac{(-1)^n(a+in)}{n^2+a^2}e^{inx}\;\;(-\pi<x<\pi)$$
$x=0$ を代入すると$$1=\frac{\sinh a\pi}{\pi}\sum^\infty_{n=-\infty}\frac{(-1)^n(a+in)}{n^2+a^2}$$$n$ を0,正,負でばらして計算すると虚部が消えます.$$\frac{\pi}{a\sinh a\pi}=\frac{1}{a^2}+2\sum_{n=1}^\infty\frac{(-1)^n}{n^2+a^2}$$以上から
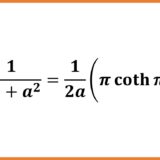
\begin{equation}\sum_{n=1}^\infty\frac{(-1)^n}{n^2+a^2}=\frac{1}{2a}\left(\frac{\pi}{\sinh a\pi}-\frac{1}{a}\right)\tag{4}\end{equation}
まさか単なる指数関数からこのような無限級数が得られるとは.フーリエ級数は世界をぐんと広げてくれますね.
似た記事:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。