初歩からの微分方程式。全20回です。
【D1】1階線型微分方程式の解法
【D2】ベルヌーイの微分方程式
【D3】クレローの方程式と包絡線(解法と例題)

【D4】Chrystalの微分方程式と包絡線
【D5】斉次2階線型微分方程式
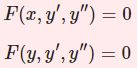
【D6】$y$または$x$を含まない2階方程式(階数低減法)
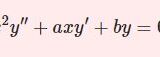
【D7】オイラー・コーシーの方程式
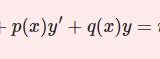
【D8】非斉次2階線型微分方程式その1
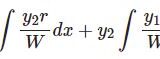
【D9】非斉次2階線型微分方程式その2
【D10】高階線型微分方程式の指針と例題
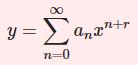
【D11】級数法・フロベニウス法
【D12】ルジャンドルの微分方程式
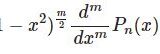
【D13】ルジャンドルの陪微分方程式
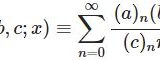
【D14】超幾何微分方程式とフロベニウス法・超幾何関数
【D15】合流型超幾何微分方程式とフロベニウス法
【D16】Whittakerの微分方程式
【D17】超幾何微分方程式への変換例
【D18】ベッセルの微分方程式と級数解
【D19】変形ベッセル微分方程式
【D20】球ベッセルの微分方程式
順に読むことをおすすめします。
フックス型微分方程式と確定特異点2 (RiemannのP方程式)
1階の非線型微分方程式 - 完全微分方程式・積分因子と具体例
y'=(Ax+By+E)/(Cx+Dy+F)の形の微分方程式
上のシリーズに入らなかったもの。
Anger関数とWeber関数②(ベッセル微分方程式の非斉次解)
座標変換や物理の方程式によくあるもの。
- y'=(Ax+By+E)/(Cx+Dy+F)の形の微分方程式非線型微分方程式シリーズ。前回はこちら: \begin{equation}\frac{dy}{dx}=\fra ...
- ポリトロープとレーン・エムデン方程式球対称な密度分布をもつ流体の天体を考えます。例えば太陽のようなガスでできている恒星とか。恒星は中心の密度が一番 ...
- 1階の同次形微分方程式(非線型)1階非線型微分方程式の同次形の場合の解法。積分因子によって完全方程式を得る方法をまず説明しますが、実践的には変数変換で簡単化する方法がありますので、そちらも紹介します。
- 1階の非線型微分方程式 - 完全微分方程式・積分因子と具体例非線型微分方程式シリーズです。前回はこちら; 今回は1階非線型微分方程式について。特に完全微分方程式によるアプ ...
- 曲線の式から非線型微分方程式をつくる非線型微分方程式を解くのはもちろん難しい。ここでは逆に、解から方程式をつくり、非線型方程式の現れ方に馴染んでみよう。その形がいかに予測困難かを実感することも含めて。
- 1階非線型微分方程式の例$$\frac{dy}{dx}=y^2+x$$非線型微分方程式の有名なカテゴリ「Riccati型」の例題を解く。
- フックス型とHeunの微分方程式$$u''+\left(\frac{\a}{z}+\frac{\b}{z-1}+\frac{\g}{z-a}\right)u'+\frac{\d\d'z+I}{z(z-1)(z-a)}u=0$$確定特異点を4個もつ任意の2階フックス型微分方程式は、Heunの微分方程式に帰着することを示す。
- 4個の確定特異点をもつフックス型微分方程式確定特異点が4個あるフックス型微分方程式の形を導出する。3個の場合との共通点が見出せる一方、アクセサリー・パラメータなる要素が初めて現れる。
- リーマンのP方程式と24個の特殊解リーマンのP微分方程式と超幾何微分方程式について、Kummerの24解を導出する。24解を必要に応じて線型結合することで数多の変換公式を得る。
- リーマンのP方程式とメビウス変換・超幾何関数2階フックス型微分方程式で確定特異点が3つであるリーマンのP方程式は、メビウス変換によって特異点が移動する以外は不変であることを示す。その結果、すべての方程式が超幾何微分方程式に帰着する。
- フックス型微分方程式とメビウス変換2階のフックス型微分方程式をメビウス変換しても不変であることを用いて、シンプルな方程式に帰着させる理論と応用。今回は確定特異点が2つ以下の場合を論じる。
- リーマンのP微分方程式の指数と解の関係フックス型であるリーマンのP方程式について、確定特異点と解の形の関係をフロベニウス法と絡めて考察する。特異点に属する「指数」とは何であろうか。無限遠が特異点である場合についても丁寧に解説。
- フックス型微分方程式と確定特異点2 (RiemannのP方程式)確定特異点を2つもつ一般的な2階フックス型微分方程式を導出する。それを足掛かりに確定特異点が3つの場合について考察し、リーマンのP方程式を導く。
- フックス型微分方程式と確定特異点1(基本と例題)フックス型の2階微分方程式と確定特異点との関係について考察する。いずれはガウスの超幾何関数にもちこむ。
- Anger関数とWeber関数②(ベッセル微分方程式の非斉次解)Bessel関数とよく似たAnger関数とWeber関数について第2回。今回はこれらが満たす微分方程式を導出する。ベッセルの微分方程式の非斉次バージョンであることが分かる。
- 三角井戸型ポテンシャルとエアリー関数$$\mathrm{Ai}(x)=\frac{1}{\pi}\int_{0}^\infty \cos\left(\frac{u^3}{3}+ux\right)du$$シュレディンガー方程式を1次元の三角井戸型ポテンシャルについて解く。初等的には解けず、方程式をラプラス変換することで積分表示し、複素平面上で適切な経路をとって特殊解「エアリー関数」を導出する。
- 【D20】球ベッセルの微分方程式$$x^2y^{\prime\prime}+2xy'+\left[x^2-\nu(\nu+1)\right]y=0$$フロベニウス法等により2つの球ベッセル関数 $j_\nu(x)$ , $n_\nu(x)$ を得るが,これらはベッセル関数と深い関りがあることを解説.整数次の場合の級数表示や具体的な関数形も求める.
- 【D19】変形ベッセル微分方程式$$x^2y^{\prime\prime}+xy'-(x^2+\nu^2)y=0$$特殊解は変形ベッセル関数とよばれ,ベッセル関数とよく似た性質を持つ.変形ベッセル関数の式を示し,半整数次では初等関数であることを解説.
- 【D18】ベッセルの微分方程式と級数解$$x^2y^{\prime\prime}+xy'+(x^2-\nu^2)y=0$$フロベニウス法により解く.代表的な特殊解は第1種ベッセル関数と第2種ベッセル関数である.例題では異なる形の方程式が,適切な変数変換によりベッセルの微分方程式に帰着する多様な例を見る.漸化式や初等関数になる例も示す.
- 【D17】超幾何微分方程式への変換例$$(t^2+pt+q)\frac{d^2y}{dt^2}+(rt+s)\frac{dy}{dt}+Ky=0$$適切な変換によりガウスの超幾何微分方程式に書き直せる.例題2つあり.
- 偶奇統一!第1種ルジャンドル関数$$P_\nu(x)= {}_2F_1\left[\begin{matrix}\nu+1,-\nu\\1\end{matrix}\;;\frac{1-x}{2}\right] $$これがルジャンドルの微分方程式で最強の解だ!ルジャンドルの微分方程式の特殊解をシンプルかつ偶奇統一された表現にしよう.
- 【D16】Whittakerの微分方程式$$y^{\prime\prime}+\left(-\frac{1}{4}+\frac{\kappa}{x}-\frac{\mu^2-\frac{1}{4}}{x^2}\right)y=0$$の解を導出する.変数変換により前回紹介したクンマーの合流型超幾何微分方程式へ帰着させる.求まった特殊解はWhittaker関数とよばれる.
- 【D15】合流型超幾何微分方程式とフロベニウス法$$xy^{\prime\prime}+(c-x)y'-ay=0$$一般的な解説+3つの例題.フロベニウス法によって解こう.ガウスの超幾何微分方程式と同様の手順であり,似た形の級数解を得る.
- 【D14】超幾何微分方程式とフロベニウス法・超幾何関数$$x(1-x)y^{\prime\prime}+[c-(a+b+1)x]y'-aby=0$$多様な例題あり。級数解の例として超幾何微分方程式の解き方を解説。点0で正則でないためフロベニウス法を使う。これで現れる特殊解はガウスの超幾何関数とよばれ、ポッホハマー記号を使うと記述しやすい。
- 【D13】ルジャンドルの陪微分方程式$$(1-x^2)y^{\prime\prime}-2xy'+\left[ n(n+1)-\frac{m^2}{1-x^2} \right]y=0$$特殊解の求め方を,前回の「ルジャンドル多項式」との関連で解説。その特殊解「ルジャンドル陪函数」を級数で明示.最後に第1種および第2種ルジャンドル陪函数について紹介.
- 【D12】ルジャンドルの微分方程式$$(1-x^2)y^{\prime\prime}-2xy^\prime+n(n+1)y=0$$初等的に解くのは大変だが級数法によって函数の形があきらかになる。特殊解として現れるルジャンドル多項式についても解説する。他:ライプニッツの公式、ロドリグの公式。
- 【D11】級数法・フロベニウス法$$y=\sum_{n=0}^\infty a_nx^{n+r} $$ズルい最終手段を解説。
- 【D10】高階線型微分方程式の指針と例題$$y^{(n)}+p_{n-1}(x)y^{(n-1)}+\cdots+p_0(x)y=r(x)$$3階以上の微分方程式であろうと基本はこれまでの2階微分と変わらない。それが実感できる例題を掲載。
- 【D9】非斉次2階線型微分方程式その2非斉次方程式 $y^{\prime\prime}+p(x)y'+q(x)y=r(x)$ では、斉次方程式の一般解にもう1つの特殊解を加えることで解を得る。よって「もう1つの特殊解」を見つけることがポイントとなる。今回はその方法として「定数変化法」を紹介する。
- 【D8】非斉次2階線型微分方程式その1$$y^{\prime\prime}+p(x)y'+q(x)y=r(x)$$「試行解による方法」を解説。非斉次の場合は、斉次方程式の一般解にもう1つの特殊解と足し合わせることで解を得る。ではその「もう1つの特殊解」とやらはどのようにして得られるのだろう。
- 【D7】オイラー・コーシーの方程式$$x^2y^{\prime\prime}+axy'+by=0$$斉次線型微分方程式の一種であり、すべての項が $x$ について同じ「べき」となっているものである。単純に見えて意外にも多様な解を得られるので面白い。
- 【D6】$y$または$x$を含まない2階方程式(階数低減法)2階微分方程式のうち $y$ が含まれていないバージョン $F(x,y',y^{\prime\prime})=0$ および $x$ が含まれないもの $F(y,y',y^{\prime\prime})=0$ を階数低減法によって解く方法を解説する。非斉次や非線型のものも含まれる。
- 【D5】斉次2階線型微分方程式$$y^{\prime\prime}+p(x)y' +q(x)y=0$$この一般解は2つの独立な特殊解の線型結合である。ここでは斉次の場合の基本的な解法を示す。1つ目は「特殊解」が1つ分かっているときにもう1つを求める方法。2つ目は定数係数の方程式の解法。
- 【D4】Chrystalの微分方程式と包絡線$$y'^2+Axy'+By+Cx^2=0$$クレローの方程式とも関連するChrystalの微分方程式について解説。特別な場合には一般解と特異解が現れ、特異解が一般解の包絡線となる。一般にはややこしいので解きやすいもののみを扱おう。
- 【D3】クレローの方程式と包絡線(解法と例題)$$y=xy'+f(y')$$は非線型微分方程式です。一般解のほかに「特異解」という変な解をもちます。特異解は一般解の包絡線になっています。
- 【D2】ベルヌーイの微分方程式$$y^\prime+p(x)y=q(x)y^a$$1階の非線型な微分方程式を、例題つきで紹介。非線型でありながらも、適切な変形を施すことで非斉次1階線型微分方程式へ帰着する例。
- 【D1】1階線型微分方程式の解法$$y' +p(x)y=r(x)$$今回からオーソドックスな微分方程式を概観していく。まずは1階の方程式から。まず斉次からやり、その応用として非斉次に取り組もう。高校の数学IIIの知識が前提。
- 球座標系のヘルムホルツ方程式と球ベッセル関数$$(\Delta+k^2)u(x,y,z)=0$$3次元のヘルムホルツ方程式を球座標で表示し、変数分離で解いていく。角度成分ではルジャンドル陪微分方程式と球ベッセル微分方程式が登場する。
- 球座標のラプラス方程式とルジャンドル陪微分方程式3次元ラプラス方程式 $\Delta u=0$ を極座標に変換し、変数分離により3つの微分方程式に分ける。そのうちの1つとしてルジャンドル陪微分方程式が現れる。
- 【物理数学】円筒座標のラプラス方程式とベッセル関数ラプラス方程式 $\Delta u=0$ を円筒座標系に変換する。次に変数分離して微分方程式を3つに分解する。そのうちの1つがベッセルの微分方程式になっていることを確認する。
- 【物理数学】N次元グリーン関数の解法(2)物理においてポアソン方程式などを解く場合に現れるグリーン関数 $G$ を求める方法について説明する。デルタ関数、第1種ベッセル関数、フーリエ変換などの数学トピックが詰まっていて勉強になる。この記事では4次元からはじめて一般のN次元の話へ拡張する。
- 【物理数学】N次元グリーン関数の解法(1)物理においてポアソン方程式などを解く場合に現れるグリーン関数$G$を求める方法について説明する。デルタ関数、第1種ベッセル関数、フーリエ変換などの数学トピックが詰まっており勉強になる。あせらず1次元からはじめて一般のN次元まで順にもっていく。