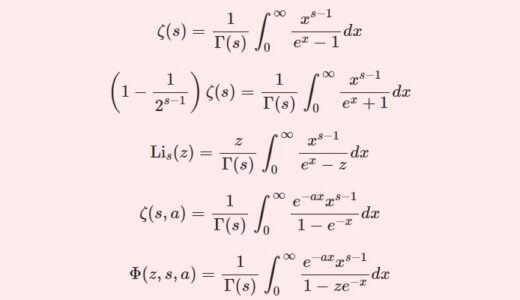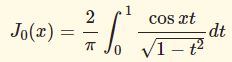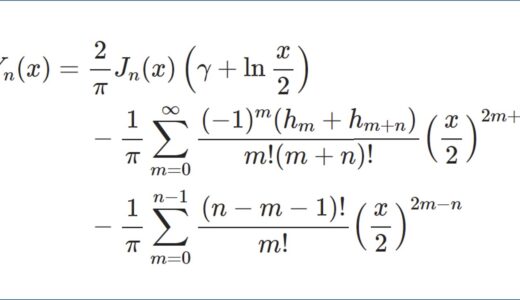微分方程式に重きを置いたもの、積分の計算など特殊関数が単なる手段であるものについては「微分方程式」「積分」カテゴリにあります。
別ページ立て。こちらへどうぞ：
調和数とEuler-sum・ゼータ関数の記事はこちらにまとめています。
ページを独立させました。
ハイパー階乗・K関数とGlaisher-Kinkelin定数①
ハイパー階乗・K関数とGlaisher-Kinkelin定数②
多くなってきたので独立させました：
- テータ関数５～ヤコビの基本関係式②前回のヤコビの基本関係式をもう少し掘り下げて、たくさんの公式を得る方法を紹介する。これまで導出した公式の上位にあるものが見えてくる。
- テータ関数４～ヤコビの基本関係式①４つのテータ関数の間にはさまざまな関係式が存在する。これらの関係式の上位には一般的な５項間関係式が存在し、次々と演繹される。
- テータ関数３～周期性と極に注目した加法定理の導出テータ関数の第3回。テータ関数を組み合わせて楕円関数をつくり、極に着目して加法定理を導出する。得た公式の特殊化・一般化についても触れる。
- テータ関数２～零点・2乗の関係テータ関数の第2回。前回導いた基本性質を使って、４つのテータ関数の零点の個数や位置、テータ関数の間で成り立つ関係式を導く。
- テータ関数１～定義と性質楕円関数ではないが二重の擬周期をもつテータ関数を解説。４つのテータ関数の最も基本的な変換公式を導出する。
- ワイエルシュトラスのペー関数９～楕円積分との関係前回はこちら： 初等的には計算できないが $\wp(z)$ を使って表すことができる積分（楕円積分）$$\in ...
- ワイエルシュトラスのペー関数８～任意の楕円関数をワイエルシュトラスの関数であらわす任意の楕円関数をワイエルシュトラスのペー関数、ゼータ関数、シグマ関数でそれぞれ表現できることを解説する。楕円関数は極や零点によって特徴づけられることが明確になる。
- ワイエルシュトラスのペー関数７～シグマ関数：擬周期性をもつ整関数ワイエルシュトラスのゼータ関数の積分で定義されるシグマ関数は、楕円関数ではないものの擬周期性をもつ整関数である。今回はこの定義と簡単な性質を解説する。
- ワイエルシュトラスのペー関数６～擬周期性をもつゼータ関数ペー関数の積分で定義されるワイエルシュトラスのゼータ関数は、最早楕円関数ではないものの、擬周期性をもつ。今回はゼータ関数の定義と簡単な性質について広く見ていく。
- ワイエルシュトラスのペー関数５~周期・不変量・アイゼンシュタイン級数の計算ワイエルシュトラスのペー関数において、周期から不変量を、あるいはその逆を導く例を解説。難しい積分とガンマ関数が現れる。同時にアイゼンシュタイン級数の計算例も説明する。
- ワイエルシュトラスのペー関数４～三次方程式との関係・半周期ワイエルシュトラスのペー関数について。導関数の零点、半周期、３次方程式と不変量について解説。
- ワイエルシュトラスのペー関数３～同次性・加法定理等ワイエルシュトラスのペー関数のシュワルツ微分、同次性、加法定理について解説。楕円関数の極や零点に関する性質を応用しよう。
- ワイエルシュトラスのペー関数２～係数の漸化式,積分公式ペー関数の級数展開において、係数にアイゼンシュタイン級数が現れる。その漸化式を導こう。またペー関数を楕円積分の逆関数として表そう。
- ワイエルシュトラスのペー関数１～基本的性質と級数展開シンプルな楕円関数であるペー関数の基本を学ぶ。関数項級数の収束性や偶奇性、周期性、展開式（アイゼンシュタイン級数）について説明する。
- 楕円関数の定義と基本的性質二重周期性によって一般の楕円関数を定義し、零点や極に関する諸性質を確認しよう。偏角の原理もここで解説。
- ヤコビの楕円関数３（二重周期性・零点・極）前回はヤコビの楕円関数３つを複素数へ拡張しました。複素関数となったからには、零点や極を知っておきたいところ。また、一般の楕円関数を定義づける二重周期性についても解説します。
- ヤコビの楕円関数２（定義域の拡張・半角公式・倍角公式・展開）３つのヤコビの楕円関数の定義域を、周期性や加法定理に注目して複素数全体にまで拡張します。さらに半角の公式や倍角の公式を導出し、三角関数や双曲線関数との類似性を確認します。
- ヤコビの楕円関数（定義・導関数・加法定理）楕円関数の初歩。「ヤコビの楕円関数」という特別なものから導入します。ヤコビの楕円関数は、三角関数と類似の性質をもつので親しみやすいです。
- ハイパー階乗・K関数とGlaisher-Kinkelin定数②$$A=\lim_{n\to\infty}\frac{H(n)\:e^{\frac{n^2}{4}}}{n^{\frac{n^2}{2}+\frac{n}{2}+\frac{1}{12}}}$$K関数の特殊値や対数K関数の積分について、Glaisher-Kinkelin定数のさまざまな表示について説明します。
- ハイパー階乗・K関数とGlaisher-Kinkelin定数①Kinkelinの論文に沿って、階乗よりもさらに巨大な数を表すハイパー階乗、およびそれを複素数まで拡張したK関数に関する等式を導出。そこで現れるGlaisher-Kinkelin定数も紹介。
- 超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値３$$\sum_{n=1}^\infty\frac{(\frac{1}{2})_n^3}{n!^3}H_{2n} = \frac{\pi}{2\G^4(\frac{3}{4})}(\pi-2\ln2)$$超幾何関数pFqをパラメータで微分し、ある値を代入すると調和数を含んだ複雑な級数公式を得る。さまざまな定理に応用して公式を導いていこう。
- 超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値２$${}_8F_7\left[\begin{matrix}1,1,1+a,1+b,1+c,2+\frac{a}{2},2+2a-b-c+m,1-m\\2,1+\frac{a}{2},2+a-b,2+a-c,2+a,1+b+c-a-m,2+a+m\end{matrix};1\right]$$超幾何関数をパラメータで微分し、ゼロへの極限をとると、ディガンマ関数を含んだ特殊値公式を得る。
- 超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値１$${}_3F_2\left[\begin{matrix}1,1,\nu+1\\2,\lambda+1\end{matrix};1\right] =\frac{\lambda}{\nu}\Bigl(\psi(\lambda)-\psi(\lambda-\nu)\Bigr)$$超幾何関数をパラメータで微分し、ゼロへの極限をとると特殊値公式を得る。
- リーマンP方程式から超幾何関数の二次変換を導出$$F\left[\begin{matrix}a,a+\frac{1}{2}\\c\end{matrix};z^2\right]=(1+z)^{-2a}F\left[\begin{matrix}2a,c-\frac{1}{2}\\2c-1\end{matrix};\frac{2z}{1+z}\right]$$リーマンのP微分方程式の変換公式から、超幾何関数の2次変換公式を生み出す方法を解説する。
- 超幾何関数2F1の特殊値と楕円積分2$$F\left(\begin{matrix}\frac{1}{4},\frac{1}{2}\\\frac{3}{4}\end{matrix};\frac{80}{81}\right)=\frac{9}{5}$$Kummerの二次変換、楕円積分の理論を用いて超幾何関数2F1の値を求める方法を紹介する。
- 超幾何関数2F1の特殊値と楕円積分1$$F\left(\begin{matrix}\frac{1}{12},\frac{5}{12}\\\frac{1}{2}\end{matrix};z\right)$$Goursatの三次変換、Kummerの二次変換、楕円積分の理論を用いて求める方法を紹介。
- 超幾何関数に関するガウスの隣接関係式ガウスの超幾何関数におけるThe fifteen relations of Gauss between contiguous functionsを紹介する。
- 超幾何関数2F1の変換公式１（基本の10個）ガウスの超幾何関数には多くの変換公式がある。簡単なものから、難しい級数計算を駆使するものまで、いくつか挑戦しよう。Pfaff、Euler、Saalschütz、Baileyその他。
- ベータ関数の偏導関数 一覧(4次まで)A list of derivatives of the beta function 難易度の高い積分や級数を ...
- 多重対数関数（ポリログ）の関係式一覧・証明付き二重対数関数、多重対数関数（ポリログ）の特殊値や関数等式の紹介と証明。logを含んだ積分をうまく扱おう。
- ベータ関数の逆数の積分表示（複素積分演習）$$\int_0^\frac{\pi}{2}\cos^{p+q-2}\t\cos(p-q)\t d\t=\frac{\pi}{2^{p+q-1}(p+q-1)B(p,q)}$$半円から3点をくりぬいた複雑な経路であるが、計算は平易である。ここで得た公式からcosの実数乗のフーリエ展開が可能となる。
- ガンマ関数の逆数のテイラー展開（微分の繰り返し・係数の積分表示）$$\frac{1}{\G(x)}=x+\g x^2+\left(\frac{\g^2}{2}-\frac{\pi^2}{12}\right)x^3+\frac{4\zeta(3)-\pi^2\g+2\g^3}{12}x^4\cdots$$ゴリゴリ微分する方法、漸化式を使う方法、積分表示する方法を学ぼう。
- 一般化された超幾何関数とベータ関数の微分の関係$${}_{p+1}F_p\left[\begin{matrix}a,a,\cdots,a,b\\a+1, a+1,\cdots, a+1\end{matrix};1\right]=-\frac{(-a)^p}{(p-1)!}\left.\frac{d^{p-1}}{dx^{p-1}}B(x,1-b)\right|_{x=a}$$を証明し、例題をやってみよう。
- 二重対数関数(dilogarithm)の等式(lntanhの積分と相反公式)$$\mathrm{Li}_2(\sqrt{2}-1)-\mathrm{Li}_2(1-\sqrt{2})=\frac{\pi^2}{8}-\frac{1}{2}\ln^2(\sqrt{2}+1)$$logtanhの積分を効果的に置換し、二重対数関数の相反公式等を用いる。
- 重積分を用いたバーゼル問題の解法②（ゼータ関数・座標変換）$$\int_0^1\int_0^1\frac{dxdy}{1-x^2y^2}$$を使ってゼータの値を計算する。この重積分の一般化とそれに向けた課題にも少し触れる。
- 重積分を用いたバーゼル問題の解法（ゼータ関数・座標軸の回転）重積分\begin{equation}I\equiv\int_0^1\int_0^1\frac{dxdy}{1-xy}\tag{1}\end{equation}を用いて$$\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}$$を示そう。
- 【ζ9】実部が正でのフルヴィッツゼータ関数の不等式・無限遠でのふるまい(ゼータ関数の基礎9)$$|\zeta(s,a)|<\frac{1}{a^\sigma}+\int_0^{\lfloor t\rfloor}\frac{dx}{(x+a)^\sigma}+\frac{1}{|t||\lfloor t\rfloor +a|^{\sigma-1}}+|s|\int^\infty_{\lfloor t\rfloor -1}\frac{dx}{(x+a)^{\sigma+1}}$$を導出する。またこれを用いて、$s$ の虚部が大きいときのゼータ関数のふるまいについて調べる。
- 【ζ8】ゼータ関数・全平面におけるRiemannの積分表示(複素積分・クシー関数)(ゼータ関数の基礎8)$$\zeta(s)\G\left(\frac{s}{2}\right)\pi^{-\frac{s}{2}}-\frac{1}{s(s-1)}=\int_1^\infty(x^{\frac{1-s}{2}}+x^{\frac{s}{2}})\vartheta(x)\frac{dx}{x}$$は任意の $s$ で成立し、クシー関数へとつながる。ガンマ関数の定義からスタートし、優収束定理、複素積分、極限計算などを使って導出できる。
- 【ζ7】ゼータ関数と素数・オイラー積・絶対収束(ゼータ関数の基礎7)$$\prod_{p}\left(1-\frac{1}{p^s}\right)=\frac{1}{\zeta(s)}$$ゼータ関数から素数の倍数を省いていくと得られる。このことからゼータ関数は実部が１より大きな領域に零点を持たないことが分かる。
- 【ζ6】フルヴィッツゼータ関数のHermiteの公式(積分表示・Abel-Planaの和公式・ビネの公式)(ゼータ関数の基礎6)$$\zeta(s,a)=\frac{1}{2a^s}+\frac{a^{1-s}}{s-1}+2\int_0^\infty\frac{\sin\left(s\arctan\frac{y}{a}\right)}{(a^2+y^2)^{\frac{s}{2}}(e^{2\pi y}-1)}dy$$エルミートの公式を導出する。極限で消える積分項の評価に苦労した。$s\to1$ の極限を調べるときにはビネの第2公式を使う。また$s=0$における微分係数も計算する。
- 【ζ5】リーマンゼータ関数の特殊値・関数等式とクシー関数・零点・全平面への接続（ゼータ関数の基礎5）$$2^{1-s}\G(s)\zeta(s)\cos\frac{\pi s}{2}=\pi^s\zeta(1-s)$$この等式は全平面で成立する。これを用いてゼータ関数の偶数での値や、零点の位数を求めてみよう。
- 【ζ4】フルヴィッツゼータ関数のフーリエ展開・複素積分・Critical Stripへの拡張(ゼータ関数の基礎4)$$\zeta(s,a)=\frac{2\G(1-s)}{(2\pi)^{1-s}}\left[\sin\frac{\pi s}{2}\sum_{n=1}^\infty\frac{\cos2\pi na}{n^{1-s}}+\cos\frac{\pi s}{2}\sum_{n=1}^\infty\frac{\sin2\pi na}{n^{1-s}}\right]$$Hurwitzゼータ関数のフーリエ展開を導出。ポイントは留数計算と、大きな円弧の積分値が0であることを示すことにある。
- 【ζ3】ハンケル路によるフルヴィッツゼータ関数の値を求める・ベルヌーイ多項式・留数定理(ゼータ関数の基礎3)$$\zeta(-m,a)=-\frac{B_{m+1}(a)}{m+1}$$$B_m(a)$ はベルヌーイ多項式。前回の積分表示を $s$ が非正整数の場合に実際に計算する。途中でベルヌーイ多項式や留数定理を用いる。
- 【ζ2】フルヴィッツゼータ関数のハンケル路による積分表示・解析接続・留数計算(ゼータ関数の基礎2)$$\zeta(s,a)=-\frac{\G(1-s)}{2\pi i}\int_C\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz$$ガンマ関数のときも現れたハンケル積分路による表現。これと前回の事実を合わせると、$s=1$を除く全平面に解析接続される。
- 【ζ1】フルヴィッツゼータ関数の積分表示（ゼータ関数の基礎1）$$\zeta(s,a)=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}e^{-ax}}{1-e^{-x}}dx$$「ゼータ関数の基礎」シリーズ初回。ゼータ関数の積分表示３つを、巧みな変数変換、総和によって導出する。
- ベータ関数のポッホハマー積分路を用いた積分表示（ガンマ関数論・複素積分）$$B(\a,\b)=-\frac{e^{-\pi i(\a+\b)}}{4\sin\pi\a\sin\pi\b}\oint_Pt^{\a-1}(1-t)^{\b-1}dt$$ポッホハマー積分路によるベータ関数の表示。ガンマ関数のハンケル表示を導出する方法と非常によく似ている。偏角に注意して積分を実行する。
- 「ビネの関数」の第2階乗型級数展開（スターリング近似の剰余項・ガンマ関数論）$$\mu(x)=\sum_{m=1}^\infty\frac{c_m}{x(x+1)\cdots(x+m-1)}$$ガンマ関数におけるスターリング近似の剰余項を「ビネの関数」とよぶ。これを階乗型級数展開してみよう。
- 「ビネの関数」の第1展開とビネの第1公式（ガンマ関数）$$\log\G(x)=\left(x-\frac{1}{2}\right)\log x-x+\frac{1}{2}\log2\pi+\int_0^\infty\left(\frac{1}{e^t-1}-\frac{1}{t}+\frac{1}{2}\right)e^{-xt}\frac{dt}{t}$$スターリングの近似の剰余項（ビネの関数）を階乗型の級数に展開し、ビネの第1公式を導く。これまで紹介した導出法とはまた異なって面白い。
- 【γ20】ガンマ関数の漸近展開（ビネの第2公式・arctanの展開・スターリング級数）（ガンマ関数の基礎20）\begin{multline}\G(x)=\sqrt{\frac{2\pi}{x}}\left(\frac{x}{e}\right)^x\\\times\left[1+\frac{1}{12x}+\frac{1}{288x^2}-\frac{139}{51840x^3}-\frac{571}{2488320x^4}+O\left(\frac{1}{x^5}\right)\right]\end{multline}ビネの第2公式の積分項を級数表示し（スターリング級数）、その級数から最初の数項だけ用いることで上式を得る。
- 【γ19】対数ガンマ関数におけるビネの第2公式の導出（アベル・プラナの和公式,ポリガンマ関数）（ガンマ関数の基礎19）$$\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi+2\int_0^\infty\frac{\arctan\frac{t}{z}}{e^{2\pi t}-1}dt$$アベル・プラナの和公式を使って導出する。複素関数を扱うが、形式的には初等的に取り組むことも可能。ガンマ関数の漸近公式へ続く。
- 【γ18】対数ガンマ関数のフーリエ級数表示（ガンマ関数の基礎18）$$\log\G(x)=\frac{1}{2}\log\pi-\frac{1}{2}\log\sin\pi x+\frac{1}{\pi}\sum_{n=1}^\infty\frac{1}{n}(\g+\log2n\pi)\sin2n\pi x$$前回の「クンマーの公式」をスタートに、フーリエ展開を用いて導出する。
- 【γ17】ガンマ関数のクンマーによる積分表示$$2\log\G(x)=\log\pi-\log\sin\pi x+\int_0^\infty\left[\frac{\sinh(\frac{1}{2}-x)t}{\sinh \frac{t}{2}}+(2x-1)e^{-t}\right]\frac{dt}{t}$$ディガンマ関数の積分表示を出発点として、対数ガンマ関数の３つの積分表示を順に導出する。最後のKummerの公式は次回のフーリエ展開へ繋がる。
- 【γ16】ビネの第1公式（導出が技巧的！）$$\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi+\int_0^\infty\left(\frac{1}{e^t-1}-\frac{1}{t}+\frac{1}{2}\right)e^{-zt}\frac{dt}{t}$$を導出する。この式では $z$ の絶対値が大きいときに積分項を無視したよい近似ができる。技巧的な積分の扱いをいろいろと学べる題材である。
- 【γ15】ディガンマ関数の積分表示３選$$\psi(z)=\int_0^\infty\left(\frac{e^{-t}}{t}-\frac{e^{-zt}}{1-e^{-t}}\right)dt=\int_{0}^\infty\left(e^{-t}-\frac{1}{(1+t)^z}\right)\frac{dt}{t}=\int_0^1\left(-\frac{1}{\log t}-\frac{t^{z-1}}{1-t}\right)dt$$前回示したオイラー定数の積分表示を用いる。やはり巧妙な技がいるものの、初等的であり高校数学でも理解できる。
- 【γ14】オイラー定数の積分表示２選・調和数・積分評価（ガンマ関数の基礎14）$$\g=\int_0^1\frac{1-e^{-t}-e^{-\frac{1}{t}}}{t}dt$$$$\g=\int_0^\infty\left(\frac{1}{1-e^{-t}}-\frac{1}{t}\right)e^{-t}dt$$技巧的ではあるが、ほぼ高校数学で理解できる。ディガンマ関数の下準備という位置づけ。
- 【γ13】ガンマ関数の放物線経路によるブルゲの積分表示・ハンケル路（ガンマ関数の基礎13）$$\G(z)=\frac{2a^ze^a}{\sin\pi z}\int_0^\infty e^{-ax^2}(1+x^2)^{z-\frac{1}{2}}\cos[2ax+(2z-1)\arctan x]dx$$ハンケルの積分表示の積分路を放物線にしたときに現れる。三角関数の計算がごちゃごちゃするが、式変形は初等的にできる。
- 【γ12】ガンマ関数の逆数・見た目だけは簡単な積分表示$$\frac{1}{\G(z)}=\frac{e}{\pi}\int_0^\frac{\pi}{2}\cos(z\t-\tan\t)\cos^{z-2}\t d\t$$見た目はシンプルだが、導出は複素積分を使うので難しい。ハンケル表示と絡めて議論する。
- Binetの第1公式の初等的証明（ログガンマの積分表示）後半\begin{multline}\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi\\+\int_0^\infty\left(\frac{1}{e^t-1}-\frac{1}{t}+\frac{1}{2}\right)e^{-zt}\frac{dt}{t}\end{multline}過去の論文を参考にほぼ高校数学の知識で分かりやすく解説。後半戦。
- Binetの第1公式の初等的証明（ログガンマの積分表示）前半\begin{multline}\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi\\+\int_0^\infty\left(\frac{1}{e^t-1}-\frac{1}{t}+\frac{1}{2}\right)e^{-zt}\frac{dt}{t}\end{multline}過去の論文を参考にほぼ高校数学の知識で分かりやすく解説。前半戦。
- 【γ11】ガンマ関数の積分表示導出①（ハンケルとか）$$\G(z)=\frac{e^{-i\pi z}}{2i\sin\pi z}\int_C e^{-t}t^{z-1}dt$$ハンケル表示を含む、ガンマ関数の６つの積分表示をていねいに導出する。後半は複素積分を駆使しよう。
- 【γ10】ポリガンマ関数の値、極、級数表示、ゼータ関数との関係（ガンマ関数の基礎シリーズ10）$$\psi^{(n)}(z+1)=\psi^{(n)}(z)+\frac{(-1)^nn!}{z^{n+1}}$$ディガンマ関数 $\psi(z)$ およびその任意回数微分をポリガンマ関数という。ポリガンマの値や極、級数表示、ゼータとの関係を学ぼう。
- 【γ9】ディガンマ関数の相反公式・倍数公式と特殊値・ゼータ関数（ガンマ関数の基礎シリーズ9）$$\psi(1-z)-\psi(z)=\pi\cot\pi z$$ディガンマ関数についての「相反公式」「倍数公式」、それらを応用した特殊値の導出、そしてゼータ関数との関係について解説。
- 【γ8】ディガンマ関数の特殊値と極$$\psi(z)\equiv\frac{\G'(z)}{\G(z)}$$$\G(z)$が「積」タイプだとすると、ディガンマ関数 $\psi(z)$ は「和」タイプだ。ディガンマの定義を示し、整数と半整数での値を求め、極と留数を導出する。
- 【γ7】Γ(1/3),Γ(1/4),Γ(1/6)の値$$\G\left(\frac{1}{3}\right)=\left(2^\frac{4}{3}\sqrt{3}\:\pi\int_0^1\frac{dt}{\sqrt{1-t^3}}\right)^\frac{1}{3}$$などガンマ関数の５つの特殊値を積分表示する。ベータ関数を介して倍数公式や相反公式を駆使して求めよう。
- 【γ6】ログガンマの微分と4つの級数表示$$\log\G(1+z)=-\g z+\sum_{n=2}^\infty\frac{(-1)^n}{n}\zeta(n)z^n$$ガンマ関数の対数（ログガンマ）を繰り返し微分し、テイラー展開する。この際ポリガンマ関数が現れる。また、上記のような級数を４つ導出。
- 【γ5】ガンマの微分とディガンマ関数$$\G'(n)=(n-1)!\left(-\g+h_{n-1}\right)$$ガンマ関数の微分と、自然数における微分係数を導出。高階へ進むためにディガンマ関数も扱う。
- 【γ4】ガンマ関数の倍数公式とガウスの乗法公式$$\G(nz)=\frac{n^{nz}}{(2\pi)^\frac{n-1}{2}\sqrt{n}}\prod_{k=0}^{n-1}\G\left(z+\frac{k}{n}\right)$$ガンマ関数の乗積表示やベータ関数との関係を用いながら証明する。
- 【γ3】ベータ関数の定義・ガンマ関数との関係・三角関数での積分表示$$B(x,y)=\frac{\G(x)\G(y)}{\G(x+y)}$$ベータ関数とそれに関する簡単な公式を示し、ガンマ関数との関係式を導出する。例題たくさん付き。
- 【γ2】ガンマ関数の３つの乗積表示と相反公式（ガウス・オイラー・ワイエルシュトラス）$$\G(z)=\displaystyle\lim_{n\to\infty}\frac{n!n^z}{\prod_{k=0}^n(z+k)}$$など３つの乗積表示「ガウスの公式」「オイラーの公式」「ワイエルシュトラスの乗積表示」を紹介。それにより「相反公式」も導出する。
- 【γ1】ガンマ関数の定義・特殊値・解析接続・留数（ガンマ関数の基礎1）$$\G(z)=\int^\infty_0e^{-t}t^{z-1}dt$$「ガンマ関数の基礎」第1回。ガンマ関数の積分表現による定義、階乗の一般化、負の値への解析接続、極について、特殊値を解説。
- ラプラス変換でベッセル関数の積分表示を作る$$J_0(x)=\frac{2}{\pi}\int_0^1\frac{\cos xt}{\sqrt{1-t^2}}dt$$微分方程式の解を逆ラプラス変換で表すことで関数の積分表示をつくることができる。今回は0次のベッセル関数でやってみよう。
- 第2種ベッセル関数 $Y_\nu(x)$ の計算$$Y_n(x)=\displaystyle\lim_{\nu\to n}\frac{\cos\nu\pi J_\nu(x)-J_{-\nu}(x)}{\sin\nu\pi}$$整数次の第2種ベッセル関数は極限により定義される。この極限を計算して第2種ベッセル関数を級数により明示する。途中でディガンマ関数などが登場する。
- 3種類のゼータ関数・多重対数関数とガンマ関数の関係$$\zeta(s)\;,\;\mathrm{Li}_s(z)\;,\;\zeta(s,a)\;,\;\Phi(z,s,a)$$これらとガンマ関数の関係（積分表示）を導出．得られた関係式に値を代入することで特殊な定積分と無限級数の等式をたくさん得ることができる．
- ゼータ関数値の求め方３選（フーリエ級数・パーセヴァルの等式・sin無限乗積）$$\zeta(s)\equiv \sum_{n=1}^\infty\frac{1}{n^s}\quad (s\in\mathbb{C})$$$s$ が偶数のときの値を考える．フーリエ級数を用いる方法，その亜種としてパーセヴァルの等式を応用する方法，$\sin$ の無限乗積展開を用いる方法を紹介．
- ルジャンドル多項式とシュレーフリの積分表示（ローラン展開・ロドリグの公式より）$$P_n(z)=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^n}{2^n(t-z)^{n+1}}dt$$schlaefliの積分表示といわれるものを導出する．とある複素積分からルジャンドル多項式のロドリグの公式を用いるという手法である．
- ルジャンドル多項式とラプラスの積分表示（母関数とワイエルシュトラス置換）$$P_n(x)=\frac{1}{\pi}\int^\pi_0(x\pm\sqrt{x^2-1}\cos\theta)^nd\theta$$ルジャンドル多項式にはいろいろな表現があり，積分表示もその１つ．今日はラプラスの積分表示といわれるものを導出する．とある簡単な定積分から母関数を導いて無限級数を比較するという手法．