関数 $u(x,y,z)$ が3次元ラプラス方程式$$\Delta u=0$$を満たすとする。この微分方程式を円筒座標系に変換して解法を示せ。
直交座標から円筒座標への変換 $(x,y,z)\to(r,\theta,z)$ は$$\begin{cases}x&=&r\cos\theta\\ y&=& r\sin\theta\end{cases}$$で与えられます。$\displaystyle\frac{y}{x}=\tan\theta$ であることから $r,\theta$ について解くと$$\begin{cases}r&=&\sqrt{x^2+y^2}\\\theta &=& \arctan\displaystyle\frac{y}{x}\end{cases}$$それぞれを $x,y$ で偏微分すると次の関係式を得ます。
$$\frac{\partial r}{\partial x}=\frac{x}{\sqrt{x^2+y^2}}=\cos\theta$$$$\frac{\partial r}{\partial y}=\frac{y}{\sqrt{x^2+y^2}}=\sin\theta$$$$\frac{\partial\theta}{\partial x}=\frac{-\frac{y}{x^2}}{1+(\frac{y}{x})^2}=-\frac{\sin\theta}{r}$$$$\frac{\partial\theta}{\partial y}=\frac{\frac{1}{x}}{1+(\frac{y}{x})^2}=\frac{\cos\theta}{r}$$これらの式およびチェインルールによって微分作用素の変換は\begin{eqnarray*}\frac{\partial}{\partial x}&=&\frac{\partial r}{\partial x}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial x}\frac{\partial}{\partial \theta}\\&=&\cos\theta\frac{\partial}{\partial r}-\frac{\sin\theta}{r}\frac{\partial}{\partial \theta}\end{eqnarray*}
\begin{eqnarray*}\frac{\partial}{\partial y}&=&\frac{\partial r}{\partial y}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial y}\frac{\partial}{\partial \theta}\\&=&\sin\theta\frac{\partial}{\partial r}+\frac{\cos\theta}{r}\frac{\partial}{\partial \theta}\end{eqnarray*}となります。
関数 $u(x,y,z)$ のラプラシアンは$$\Delta u\equiv\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}$$円筒座標系で表示するために右辺第1,2項を $r,\theta$ に書き換えると\begin{eqnarray*}\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}&=& \left(\cos\theta\frac{\partial}{\partial r}-\frac{\sin\theta}{r}\frac{\partial}{\partial \theta}\right)\left(\cos\theta\frac{\partial u}{\partial r}-\frac{\sin\theta}{r}\frac{\partial u}{\partial \theta}\right)+\left(\sin\theta\frac{\partial}{\partial r}+\frac{\cos\theta}{r}\frac{\partial}{\partial \theta}\right)\left(\sin\theta\frac{\partial u}{\partial r}+\frac{\cos\theta}{r}\frac{\partial u}{\partial \theta}\right)\\ &=& \cos^2\theta\frac{\partial^2u}{\partial r^2}-\frac{\sin\theta}{r}\frac{\partial}{\partial\theta}(\cos\theta\frac{\partial u}{\partial r})+\frac{\sin\theta}{r^2}\frac{\partial}{\partial\theta}(\sin\theta\frac{\partial u}{\partial\theta})+\sin^2\theta\frac{\partial^2u}{\partial r^2}+\frac{\cos\theta}{r}\frac{\partial}{\partial\theta}(\sin\theta\frac{\partial u}{\partial r})+\frac{\cos\theta}{r^2}\frac{\partial}{\partial\theta}(\cos\theta\frac{\partial u}{\partial\theta})\\ &=&\frac{\partial^2u}{\partial r^2}+\frac{\sin^2\theta}{r}\frac{\partial u}{\partial r}+\frac{\sin^2\theta}{r^2}\frac{\partial^2u}{\partial \theta^2}+\frac{\cos^2\theta}{r}\frac{\partial u}{\partial r}+\frac{\cos^2\theta}{r^2}\frac{\partial^2u}{\partial \theta^2}\\ &=&\frac{\partial^2u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{\partial^2u}{\partial \theta^2}\end{eqnarray*}従って円筒座標系でのラプラシアンは$$\Delta u= \frac{\partial^2u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{\partial^2u}{\partial \theta^2}+ \frac{\partial^2u}{\partial z^2} $$と書けます。
ステップ1 $Z(z)$ の分離
ここで関数 $u(x,y,z)$ が3次元ラプラス方程式$$\Delta u=0$$を満たすとします。先ほどの議論より円筒座標系に変換すると$$\frac{\partial^2u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}+\frac{1}{r^2}\frac{\partial^2u}{\partial \theta^2}+\frac{\partial^2u}{\partial z^2}=0$$この方程式を解くために$$u(r,\theta,z)=R(r)\Theta(\theta)Z(z)$$と変数分離します。すると方程式は$$\Theta Z\left(\frac{d^2R}{dr^2}+\frac{1}{r}\frac{dR}{dr}\right)+\frac{RZ}{r^2}\frac{d^2\Theta}{d\theta^2}+R\Theta\frac{d^2 Z}{dz^2}=0$$両辺を $R\Theta Z$ で割り$$\frac{1}{R}\left(\frac{d^2R}{dr^2}+\frac{1}{r}\frac{dR}{dr}\right)+\frac{1}{r^2\Theta}\frac{d^2\Theta}{d\theta^2}+\frac{1}{Z}\frac{d^2 Z}{\partial z^2}=0$$$$\therefore\quad \frac{1}{R}\left(\frac{d^2R}{dr^2}+\frac{1}{r}\frac{dR}{dr}\right)+\frac{1}{r^2\Theta}\frac{d^2\Theta}{d\theta^2}=-\frac{1}{Z}\frac{d^2 Z}{dz^2}\tag{1}$$この左辺は $r,\theta$ の関数、右辺は $z$ の関数です。よって任意の $r,\theta,z$ で式が成り立つためには左辺と右辺が定数でなければいけません。この定数を $-k^2$ とおくと$$\frac{d^2 Z}{dz^2}=k^2Z$$$$\therefore \; Z(z)=Z_1e^{kz}+Z_2e^{-kz}\;\;(k,Z_1,Z_2\in\mathbb{C})$$
現れた定数は、実践では境界条件や初期条件によって定まります。以降も同様。
ステップ2 $\Theta(\theta)$ の分離
一方(1)の左辺すなわち $r,\theta$ の関数のほうでは$$\frac{1}{R}\left(\frac{d^2R}{dr^2}+\frac{1}{r}\frac{dR}{dr}\right)+\frac{1}{r^2\Theta}\frac{d^2\Theta}{d\theta^2}=-k^2$$が成り立っています。変形すると$$\frac{r^2}{R}\frac{d^2R}{dr^2}+\frac{r}{R}\frac{dR}{dr}+k^2r^2=-\frac{1}{\Theta}\frac{d^2\Theta}{d\theta^2}\tag{2}$$この左辺は $r$ の関数、右辺は $\theta$ の関数です。よって任意の $r,\theta$ で式が成り立つためには左辺と右辺が定数でなければいけません。この定数を $\nu^2$ とすると$$\frac{d^2\Theta}{d\theta^2}=-\nu^2\Theta$$$$\therefore\; \Theta(\theta)=A\sin\nu\theta+B\cos\nu\theta\;\;(\nu,A,B\in\mathbb{C})$$
ステップ3 ベッセルの微分方程式が出現
一方(2)の左辺すなわち $r$ の関数のほうでは$$\frac{r^2}{R}\frac{d^2R}{dr^2}+\frac{r}{R}\frac{dR}{dr}+k^2r^2=\nu^2$$
が成り立っています。変形すると$$r^2\frac{d^2R}{dr^2}+r\frac{dR}{dr}+(k^2r^2-\nu^2)R=0$$$kr=\rho$ とおくと
$$\rho^2\frac{d^2R}{d\rho^2}+\rho\frac{dR}{d\rho}+(\rho^2-\nu^2)R=0$$これはベッセルの微分方程式とよばれます。
ベッセルの微分方程式の一般解は第1種ベッセル関数 $J_\nu(\rho)$ および第2種ベッセル関数 $Y_\nu(\rho)$ の線型結合で表されます(あるいはハンケル関数を使うこともできます)。よって解は$$R(r)=R_1J_\nu(kr)+R_2Y_\nu(kr) \;\;(R_1,R_2\in\mathbb{C}) $$
ベッセルの微分方程式の解法はこちら
以上より円筒座標におけるラプラス方程式の解は\begin{eqnarray*} Z(z)&=&Z_1e^{kz}+Z_2e^{-kz}\\ \Theta(\theta)&=&A\sin\nu\theta+B\cos\nu\theta\\ R(r)&=&R_1J_\nu(kr)+R_2Y_\nu(kr) \end{eqnarray*}これらを境界条件や初期条件をもとに解くことになります。
もちろん $Z(z)=\mathrm{const.}$ などといった解もありますが、本記事では特別な条件を用いず微分方程式を「フルで」解いた場合に焦点を当てています。
$$\frac{\partial^2u}{\partial t^2}(x,y,z,t)=c^2\Delta u(x,y,z,t)$$を円筒座標系 $(r,\theta,z)$ に変換し、変数分離 $u=R(r)\Theta(\theta)Z(z)T(t)$ によって解にベッセル函数が現れることを確認せよ.
球座標でもやってみました↓
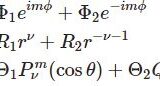 球座標のラプラス方程式とルジャンドル陪微分方程式
球座標のラプラス方程式とルジャンドル陪微分方程式
ベッセル関数に関する記事
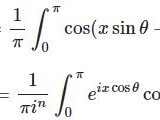 第1種ベッセル関数の積分表示とその導出
第1種ベッセル関数の積分表示とその導出
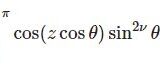 第1種ベッセル関数の積分表示(2) ポアソンの公式の導出
第1種ベッセル関数の積分表示(2) ポアソンの公式の導出
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。

いつもご式展開,参考にさせていただいております.
ありがとうございます.
質問させていただけましたら幸いです.
(1)式の下の文言
「任意の r,θ,z で式が成り立つためには左辺と右辺が定数でなければいけません」
とはどういう意味でしょうか.
方程式がある変数の時だけ成り立つ等式ではなく,
任意の値で成り立つ等式=「恒等式」の場合を考えると,
定数になるという意味でしょうか.
そうだとしても何故定数出ないといけないのかまで理解できていないのですが,
もしよろしければお手すきの際にご教示いただけますと幸いです.
ご拝読いただき,ありがとうございました.
お読みいただきありがとうございます。
例えばx,yという2つの独立変数があってf(x)=g(y)という式が成立したとします。x,yがまったく独立で、任意の値で式が成立する必要があるので、おっしゃるとおり「恒等式」でなくてはいけません。ここで、もしf(x)とg(y)が定数でないとするとxとyに関係式ができてしまいます。
定数でない場合、例えば x^2=y^3+1 なら、x=0のときはy=-1でないといけなくなり、独立でなくなってしまいます。
という感じで、両辺は定数と考えられます。