微分幾何学の講座・第8回。曲面の曲がり具合を表す尺度として「主曲率」や「平均曲率」「ガウス曲率」を紹介します。前回の法曲率をもとに計算します。
前回はこちら:
曲面上の点 $\bm{S}(u(s),v(s))$ における法曲率を次で定義する。\begin{equation}\kappa_n(s):=\bm{S}''\bigl(u(s),v(s)\bigr)\cdot \bm{n}\bigl(u(s),v(s)\bigr)\tag{1}\end{equation}
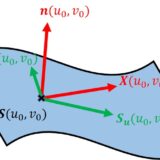
曲面 $\bm{S}(u,v)$ 上の点P $=\bm{S}(u_0,v_0)$ の単位接ベクトル $\bm{X}(u_0,v_0)$ を定めます。また $u$ , $v$ 方向の接ベクトル $\bm{S}_u$ , $\bm{S}_v$ および単位法ベクトル $\bm{n}(u_0,v_0)$ が定まります。$\bm{X}(u_0,v_0)$ と $\bm{n}(u_0,v_0)$ が張る平面と曲面 $\bm{S}(u,v)$ の交線 $c(s)$ の(平面曲線としての)曲率 $\kappa_n(s)$ を、曲面の点Pにおける $\bm{X}$ 方向の法曲率とよびます。ただし $s$ は弧長パラメータです。

前回に見たように、接ベクトル $\bm{X}$ の向きによって法曲率は異なります。$\bm{X}$ を動かしたときの法曲率の最大値 $\kappa_1$および最小値 $\kappa_2$ を主曲率といいます。また法曲率が $\kappa_1$ あるいは $\kappa_2$ となる $\bm{X}$ の方向を主方向とよびます。
法曲率の定義は(1)ですが、実際の計算には次の式を使うのでした。
\begin{equation}\kappa_n=\frac{\mathrm{II}}{\mathrm{I}}\tag{2}\end{equation}
ここで $\mathrm{I}$ , $\mathrm{II}$ は第1基本形式および第2基本形式です。\begin{equation}\mathrm{I}:=Edu^2+2Fdudv+Gdv^2\tag{3}\end{equation}\begin{equation}\mathrm{II}:=Ldu^2+2Mdudv+Ndv^2\tag{4}\end{equation}
接ベクトルの表式$$\bm{X}=\bm{S}_udu+\bm{S}_vdv$$より $\bm{X}$ の方向は $du$ と $dv$ の比で定まります。例えば $dv=0$ とおくと $\bm{X}$ は $\bm{S}_u$ の方向になります。法曲率の最大値と最小値を求めるには、$du=\a$ , $dv=\b$ とおくと\begin{equation}\kappa_n=\frac{L\a^2+2M\a\b+N\b^2}{E\a^2+2F\a\b+G\b^2}\tag{5}\end{equation}となり、この極値を調べるとよいです。
いま、$$f(\a,\b):=\frac{L\a^2+2M\a\b+N\b^2}{E\a^2+2F\a\b+G\b^2}\;,\quad(\a,\b)\neq(0,0)$$とします。微分すると\begin{eqnarray*}f_\a &=& \frac{\b\{(FL-EM)\a^2+(GL-EN)\a\b+(GM-FN)\b^2\}}{(E\a^2+2F\a\b+G\b^2)^2}\\f_\b&=& \frac{\a\{(FL-EM)\a^2+(GL-EN)\a\b+(GM-FN)\b^2\}}{(E\a^2+2F\a\b+G\b^2)^2}\end{eqnarray*}$(\a,\b)$ で極値をとるなら $f_\a=f_\b=0$ なので$$(FL-EM)\a^2+(GL-EN)\a\b+(GM-FN)\b^2=0$$$\g=\b/\a$ とおくと2次方程式になります。$$(FL-EM)+(GL-EN)\g+(GM-FN)\g^2=0$$\begin{equation}\therefore\quad\g=\frac{EN-GL\pm\sqrt{(GL-EN)^2-4(GM-FN)(FL-EM)}}{2(GM-FN)}\tag{6}\end{equation}(6)を(5)に代入することで2つの主曲率が得られます。しかし、計算するのは嫌ですね。
主曲率 $\kappa_1$ , $\kappa_2$ を用いて平均曲率 $H$ とガウス曲率 $K$ を次で定める。\begin{equation}H:=\frac{\kappa_1+\kappa_2}{2}\quad,\quad K:=\kappa_1\kappa_2\tag{7}\end{equation}
前節を見て分かる通り、主曲率の計算は面倒ですし、たぶんきれいな式にならないと思います。
そこで、2つの解(6)を用いて $H$ と $K$ を計算します。これはこれで大変ですのでMaximaにやらせました。すると\begin{eqnarray}H &=& \frac{EN-2FM+GL}{2(EG-F^2)}\tag{8} \\ K &=& \frac{LN-M^2}{EG-F^2}\tag{9}\end{eqnarray}を得ます。
ところで第1基本行列 $\mathcal{G}$ と第2基本行列 $\mathcal{H}$ は\begin{equation}\mathcal{G}=\begin{pmatrix}E & F \\ F & G\end{pmatrix}\quad,\quad\mathcal{H}=\begin{pmatrix}L & M \\ M & N\end{pmatrix}\tag{10}\end{equation}と定義されるのでした。これらより作られる行列\begin{equation}\mathcal{H}\mathcal{G}^{-1}=\frac{1}{EG-F^2}\begin{pmatrix}GL-FM & EM-FL \\ GM-FN & EN-FM\end{pmatrix}\tag{11}\end{equation}を考えると、(8)(9)は\begin{eqnarray}H &=& \frac{1}{2}\mathrm{tr}\left(\mathcal{HG}^{-1}\right)\tag{12} \\ K &=& \det\left(\mathcal{HG^{-1}}\right)\tag{13}\end{eqnarray}とも表せます。地道な計算で容易に示せます。
曲面の領域 $A$ 上の各点で、ガウス曲率 $K$ を足し合わせたものを全曲率といいます。ただし「ガウス曲率=全曲率」と呼称することも多いようで、一般にどのように区別しているのかはよく分かりません。
$$K_{\mathrm{total}}=\iint_A KdA$$
$\kappa_1=\kappa_2$ になるような点を曲面の臍点(umbilic)とよびます。要は「特別な2方向」がなく、全ての方向に対して曲面が同じように曲がっているのです。
また $K>0$ となる点を楕円点といい、曲面は凸になります。$K=0$ となる点を放物点といいます。$K<0$ となる点を双曲点とよび、曲面は鞍状になります。(9)から直ちに分かるように、$K$ の符号は $LM-N^2$ の符号 に一致します。
半径 $a$ の球面$$\bm{S}(u,v):=\bigl(a\cos u\cos v,a\cos u\sin v, a\sin u\bigr)\;,\;-\frac{\pi}{2}\le u \le\frac{\pi}{2}\:,\:0\le v<2\pi$$の主曲率・平均曲率・ガウス曲率を求めよ。
また北極から南へ進んで赤道へ至り、赤道に沿って東に90°回り、再び北極に至る球面三角形を考える。この三角形内の全曲率はいくらか。
前回記事より法曲率は $\kappa_n=1/a$ (定数)ですので、2つの主曲率も同じ値です。よって$$\kappa_1=\kappa_2=H=\frac{1}{a}\;,\; K=\frac{1}{a^2}$$問題の全曲率は$$K_{\mathrm{total}}=\frac{1}{a^2}\iint dA=\frac{1}{a^2}\cdot \frac{\pi a^2}{2}=\frac{\pi}{2}$$この球面三角形の内角の和が270°で、平面三角形のそれより $\pi/2$ 大きいことと関係しています。
楕円放物面$$\bm{S}(u,v):=\bigl(au,bv, u^2+v^2\bigr)\;,\quad u,v\in\RR$$のガウス曲率を求めよ。
過去記事より$$E=a^2+4u^2\;,\;F=4uv\;,\; G=b^2+4v^2$$$$L=N=\frac{2ab}{\sqrt{4b^2u^2+4a^2v^2+a^2b^2}}\;,\;M=0$$(9)より$$K=\frac{4a^2b^2}{(a^2b^2+4b^2u^2+4a^2v^2)^2}$$
・中内伸光『幾何学は微分しないと』(下記)
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。初学者向けな分、内容はやや薄いと思うので、ネットや他の書籍を併用すると学習効果が高まります。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
次:
 ガウスの公式とワインガルテンの公式
ガウスの公式とワインガルテンの公式
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
