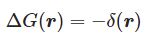ベッセルの微分方程式の解である第1種ベッセル関数は、さまざまな場面で登場します。しかしその登場するシーンによって姿を変えるためになかなか奥深いのです。過去に$N$次元グリーン関数の記事を書きましたが、そこではこのベッセル関数が積分表示されたもの(Hansen-Besselの公式)が現れました。そのときは公式の証明をせずに使ってしまったので、補完したかったというのが本記事の動機です。
第1種ベッセル関数 $J_\nu(x)$ は複素数の添え字 $\nu$ をもちますが、整数 $n$ である場合は以下の級数表示をもちますので、これを出発点として展開していきましょう。
非負整数 $n$ に対し\begin{equation}J_n(x)=\sum^\infty_{m=0}\frac{(-1)^m}{m!(m+n)!}\left(\frac{x}{2}\right)^{2m+n}\tag{1}\end{equation}\begin{equation}J_{-n}(x)=(-1)^nJ_n(x)\tag{2}\end{equation}
そもそもベッセル関数とは何なのか,どうしてこんな級数になるのかは別記事参照です.
(1) Besselの積分表示\begin{equation}J_n(x)=\frac{1}{\pi}\int^\pi_0\cos(x\sin\theta-n\theta)d\theta\end{equation}
(2) Hansen-Besselの公式\begin{equation}J_n(x)=\frac{1}{\pi i^n}\int^\pi_0e^{ix\cos\theta}\cos n\theta d\theta\end{equation}を導出する.
(3) $\nu,z\in\CC$ へ拡張した積分表示は$$J_\nu(z)=\frac{(z/2)^\nu}{2\pi i}\int_{-\infty}^{(0+)}t^{-\nu-1}e^{t-\frac{z^2}{4t}}dt$$ただし積分路は $-\infty$ を出発し、実軸に沿って原点へ向かい、原点まわりを正方向に周り、実軸に沿って $-\infty$ へ向かう(いわゆるハンケル積分路)。
方針は、まず第1種ベッセル関数が係数となるような、ある関数のローラン展開を行います。あとは平易な複素積分と式変形です。
\begin{equation}e^{\frac{x}{2}(z-\frac{1}{z})}=\sum^{\infty}_{n=-\infty}J_n(x)z^n\end{equation}
左辺をローラン展開するとベッセル関数が係数として現れるという意味の式であり、左辺を $J_n(x)$ の母関数といいます。この式はベッセル関数のさまざまな表示を導出するときに使われるものです。まずはこれを示しましょう。
\begin{eqnarray*} e^{\frac{x}{2}(z-\frac{1}{z})} &=& e^{\frac{x}{2}z}e^{-\frac{x}{2z}}\\&=&\sum^\infty_{l=0}\frac{(\frac{x}{2}z)^l}{l!} \sum^\infty_{m=0}\frac{(-\frac{x}{2z})^m}{m!}\\&=&\sum^\infty_{l=0}\sum^\infty_{m=0}\frac{(-1)^m}{l!m!}\left(\frac{x}{2}\right)^{l+m}z^{l-m}\end{eqnarray*} $l\ge m$ のときと $l<m$ のときで分けます。\begin{equation} e^{\frac{x}{2}(z-\frac{1}{z})} = \sum^\infty_{l\ge m}\sum^\infty_{m=0} \frac{(-1)^m}{l!m!}\left(\frac{x}{2}\right)^{l+m}z^{l-m} + \sum^\infty_{m>l}\sum^\infty_{l=0} \frac{(-1)^m}{l!m!}\left(\frac{x}{2}\right)^{l+m}z^{l-m}\end{equation}第1項で $l=m+n$ , 第2項で $m=l+n$ とおくと \begin{eqnarray*} e^{\frac{x}{2}(z-\frac{1}{z})} &=& \sum^\infty_{n=0}\sum^\infty_{m=0} \frac{(-1)^m}{(m+n)!m!}\left(\frac{x}{2}\right)^{2m+n}z^n + \sum^\infty_{n=1}\sum^\infty_{l=0} \frac{(-1)^{l+n}}{l!(l+n)!}\left(\frac{x}{2}\right)^{2l+n}z^{-n}\\&=& \sum^\infty_{n=0} J_n(x)z^n+\sum^\infty_{n=1}(-1)^nJ_n(x)z^{-n}\;\because(1)\\&=& \sum^\infty_{n=0} J_n(x)z^n+\sum^\infty_{n=1}J_{-n}(x)z^{-n}\;\because(2)\\&=& \sum^\infty_{n=-\infty} J_n(x)z^n\end{eqnarray*} というわけです。この関係式を使ってゴールを目指します。
先ほどの関係式の添え字を変更しておきます。\begin{equation}e^{\frac{x}{2}(z-\frac{1}{z})}=\sum^{\infty}_{m=-\infty}J_m(x)z^m\end{equation} 両辺に $z^{-n-1}$ をかけ、単位円 $|z|=1$ 上で複素積分します。$$\oint_{|z|=1}z^{-n-1}e^{\frac{x}{2}(z-\frac{1}{z})}dz= \sum^{\infty}_{m=-\infty}J_m(x)\oint_{|z|=1}z^{m-n-1}dz$$ $z=e^{i\theta}$ と置換すると $dz=ie^{i\theta}d\theta$ ですので\begin{eqnarray*} &&\oint_{|z|=1}z^{-n-1}e^{\frac{x}{2}(z-\frac{1}{z})}dz= \sum^{\infty}_{m=-\infty}J_m(x)\oint_{|z|=1}z^{m-n-1}dz\\&\Leftrightarrow&\int^{2\pi}_0e^{-i(n+1)\theta}e^{x\frac{e^{i\theta}-e^{-i\theta}}{2}}ie^{i\theta}d\theta=\sum^{\infty}_{m=-\infty}J_m(x)\int^{2\pi}_0e^{i(m-n-1)\theta}ie^{i\theta}d\theta\\ &\Leftrightarrow& \int^{2\pi}_0e^{-in\theta}e^{ix\sin\theta}d\theta=\sum^{\infty}_{m=-\infty}J_m(x)\int^{2\pi}_0e^{i(m-n)\theta}d\theta\\ &\Leftrightarrow& \int^{2\pi}_0e^{i(x\sin\theta-n\theta)}d\theta=2\pi J_n(x)\end{eqnarray*}左辺については積分区間を半分に分けた後半のほうを$\phi=2\pi-\theta$ と置換することで\begin{eqnarray*} \int^{2\pi}_0e^{i(x\sin\theta-n\theta)}d\theta&=& \int^{\pi}_0e^{i(x\sin\theta-n\theta)}d\theta+ \int^{2\pi}_\pi e^{i(x\sin\theta-n\theta)}d\theta\\&=&\int^{\pi}_0e^{i(x\sin\theta-n\theta)}d\theta+ \int^{0}_{\pi}e^{i(-x\sin\phi+n\phi)}(-d\phi)\\&=&\int^{\pi}_0e^{i(x\sin\theta-n\theta)}d\theta+\int^{\pi}_{0}e^{i(-x\sin\phi+n\phi)}d\phi \\&=&\int^{\pi}_0e^{i(x\sin\theta-n\theta)}d\theta+\int^{\pi}_{0}e^{i(-x\sin\theta+n\theta)}d\theta \\&=&\int^{\pi}_0\left(e^{i(x\sin\theta-n\theta)}+e^{-i(x\sin\theta-n\theta)}\right)d\theta\\&=& 2\int^{\pi}_0\cos(x\sin\theta-n\theta)d\theta\end{eqnarray*} $$\therefore\quad J_n(x)=\frac{1}{\pi}\int^\pi_0\cos(x\sin\theta-n\theta)d\theta$$これで今回のテーマの1つ、Besselの積分表示を導くことができました。ちなみに「Besselの積分表示」という名前は『岩波数学公式III』に書かれていたもので、普及している名前なのかは知りません。
Besselの積分表示のときに考えた複素積分 $$\oint_{|z|=1}z^{-n-1}e^{\frac{x}{2}(z-\frac{1}{z})}dz= \sum^{\infty}_{m=-\infty}J_m(x)\oint_{|z|=1}z^{m-n-1}dz$$ からはじめます。積分経路は単位円ですが、位相 $\pi/2$ からスタートととすると $z=ie^{i\theta}$ と置換することとなります。\begin{eqnarray*} &&\oint_{|z|=1}z^{-n-1}e^{\frac{x}{2}(z-\frac{1}{z})}dz= \sum^{\infty}_{m=-\infty}J_m(x)\oint_{|z|=1}z^{m-n-1}dz\\ &\Leftrightarrow&\int^{2\pi}_0i^{-n-1}e^{-i(n+1)\theta}e^{ix\frac{e^{i\theta}+e^{-i\theta}}{2}}(-e^{i\theta})d\theta=\sum^{\infty}_{m=-\infty}J_m(x)\int^{2\pi}_0i^{m-n-1}e^{i(m-n-1)\theta}(-e^{i\theta})d\theta\\ &\Leftrightarrow&\int^{2\pi}_0e^{-in\theta}e^{ix\cos\theta}d\theta=\sum^{\infty}_{m=-\infty}J_m(x)\int^{2\pi}_0i^me^{i(m-n)\theta}d\theta \\ &\Leftrightarrow& \int^{2\pi}_0e^{i(x\cos\theta-n\theta)}d\theta=2\pi i^nJ_n(x)\end{eqnarray*} 左辺については積分区間を半分に分けた後半のほうを$\phi=2\pi-\theta$ と置換することで\begin{eqnarray*} \int^{2\pi}_0e^{i(x\cos\theta-n\theta)}d\theta &=& \int^{2\pi}_0e^{i(x\cos\theta-n\theta)}d\theta+ \int^{2\pi}_\pi e^{i(x\cos\theta-n\theta)}d\theta\\&=& \int^{\pi}_0e^{i(x\cos\theta-n\theta)}d\theta+ \int^{0}_\pi e^{i(x\cos\phi+n\phi)}(-d\phi)\\&=& \int^{\pi}_0e^{i(x\cos\theta-n\theta)}d\theta+ \int^{\pi}_0 e^{i(x\cos\phi+n\phi)}d\phi\\&=& \int^{\pi}_0e^{i(x\cos\theta-n\theta)}d\theta+ \int^{\pi}_0 e^{i(x\cos\theta+n\theta)}d\theta\\&=& \int^{\pi}_0e^{ix\cos\theta}\left(e^{in\theta}+e^{-in\theta}\right)d\theta\\&=& 2\int^{\pi}_0e^{ix\cos\theta}\cos n\theta d\theta \end{eqnarray*}$$\therefore\quad J_n(x) =\frac{1}{\pi i^n} \int^{\pi}_0e^{ix\cos\theta}\cos n\theta d\theta $$ とできました。
以上で今回のテーマが達成できました。ローラン展開から複素積分まで多様な知識を応用できたと思います。
\begin{equation}J_n(x)=\frac{1}{\pi}\int^\pi_0\cos(x\sin\theta-n\theta)d\theta\end{equation}\begin{equation}J_n(x)=\frac{1}{\pi i^n}\int^\pi_0e^{ix\cos\theta}\cos n\theta d\theta\end{equation}が成立する.
$$J_l(z_1+z_2)=\sum_{n=-\infty}^\infty J_{l-n}(z_1)J_n(z_2)$$を示せ。
$$e^{\frac{z_1+z_2}{2}(t-\frac{1}{t})}=\sum^{\infty}_{l=-\infty}J_l(z_1+z_2)t^l$$左辺は次の式と等しい。\begin{eqnarray*}e^{\frac{z_1}{2}(t-\frac{1}{t})}e^{\frac{z_2}{2}(t-\frac{1}{t})} &=& \sum_{m=-\infty}^\infty J_m(z_1)t^m\sum_{n=-\infty}^\infty J_n(z_2)t^n\\ &=& \sum_{m=-\infty}^\infty\sum_{n=-\infty}^\infty J_m(z_1)J_n(z_2)t^{m+n} \\&=& \sum_{l=-\infty}^\infty\sum_{n=-\infty}^\infty J_{l-n}(z_1)J_n(z_2)t^{l}\quad(m+n:=l)\end{eqnarray*}$$\therefore\quad J_l(z_1+z_2)=\sum_{n=-\infty}^\infty J_{l-n}(z_1)J_n(z_2)$$
第1種ベッセル関数を $\nu\in\CC$ , $z\in\CC$ まで拡張した積分表示は$$J_\nu(z)=\frac{(z/2)^\nu}{2\pi i}\int_{-\infty}^{(0+)}t^{-\nu-1}e^{t-\frac{z^2}{4t}}dt$$積分路は $-\infty$ からやってきて 原点回りを正方向に周って $-\infty$ に帰っていくというもので、ハンケル積分路といいます。形は自由に変えられ、例えば下のような実軸ギリギリに沿わして小円で回るなどが有名です。被積分関数は $t=0$ に分岐点(Branch point)をもつため、負の実軸を切断(Cut)して考えます。
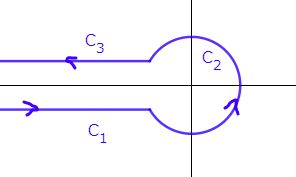
この積分はあらゆる $z$ に対して値をとるので正則です。$\nu$ が整数の場合は分岐点を持たないため、切断はありません。よって $C_1$ と $C_3$ は相殺されるので、積分路は原点を中心とする任意の半径の円とすればOKです。
$e^{-\frac{z^2}{4t}}$ を展開すると$$J_\nu(z)=\frac{(z/2)^\nu}{2\pi i}\sum_{m=0}^\infty\frac{(-1)^m(z/2)^{2m}}{m!}\int_{-\infty}^{(0+)}e^tt^{-m-\nu-1}dt$$ここで過去記事
で現れたガンマ関数の表示$$\frac{1}{\G(z)}=\frac{-1}{2\pi i}\int_{+\infty}^{(0+)} e^{-t}(-t)^{-z}dt$$で $-t\to t$ と置換したもの$$\frac{1}{\G(z)}=\frac{1}{2\pi i}\int_{-\infty}^{(0+)} e^{t}t^{-z}dt$$を用いることができて$$J_\nu(z)=\left(\frac{z}{2}\right)^\nu\sum_{m=0}^\infty\frac{(-1)^m(z/2)^{2m}}{m!\G(m+\nu+1)}$$したがって$$J_\nu(z)=\sum_{m=0}^\infty\frac{(-1)^m}{m!\G(m+\nu+1)}\left(\frac{z}{2}\right)^{2m+\nu}$$$\nu=n$ であれば$$J_n(z)=\sum_{m=0}^\infty\frac{(-1)^m}{m!(m+n)!}\left(\frac{z}{2}\right)^{2m+n}$$となり、(1)に一致しています($\nu=n$ の場合は積分路を半径1の円としてまともに積分してもOK)。よって$$J_\nu(z)=\frac{(z/2)^\nu}{2\pi i}\int_{-\infty}^{(0+)}t^{-\nu-1}e^{t-\frac{z^2}{4t}}dt$$なる表示は、これまで学んだ $J_n(z)$ を含んでおり、拡張したものであるといえます。
複素積分による表示で $\nu=n$ のときは$$J_n(z)=\frac{(z/2)^n}{2\pi i}\oint^{(0+)}t^{-n-1}e^{t-\frac{z^2}{4t}}dt$$である。ただし積分路は原点回りを正方向に周る円。これを計算して(1)と等しいことを示せ。
複素積分するためにローラン展開します。$e^{t-\frac{z^2}{4t}}$ を展開すると$$\left(1+t+\frac{t^2}{2!}+\cdots\right)\left(1-\frac{z^2}{4t}+\frac{1}{2!}\left(\frac{z^2}{4t}\right)^2+\cdots\right)$$$t^n$ の項のみを取り出すと$$t^n\sum_{m=0}^\infty\frac{(-1)^m}{m!(n+m)!}\left(\frac{z}{2}\right)^{2m}$$よって被積分関数の $t^{-1}$ の項は$$a_{-1}=\sum_{m=0}^\infty\frac{(-1)^m}{m!(n+m)!}\left(\frac{z}{2}\right)^{2m}$$積分値は $2\pi i a_{-1}$ なので結局$$J_n(z)=\sum^\infty_{m=0}\frac{(-1)^m}{m!(m+n)!}\left(\frac{z}{2}\right)^{2m+n}$$つまり(1)と等しい。
ベッセル関数の積分表示はほかにもあります.
変形ベッセル関数でも同様のことをしました.
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。