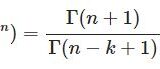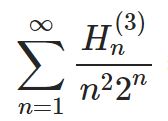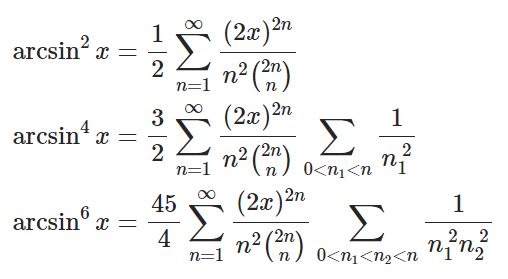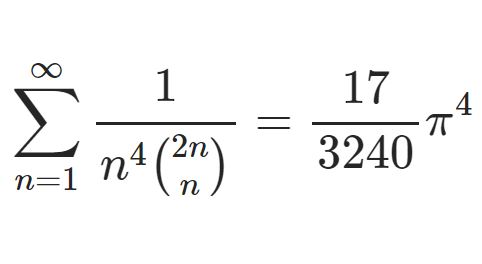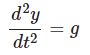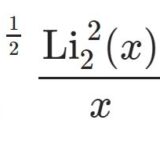
logを含む難しい積分18(多重対数関数の積分ふくむ)
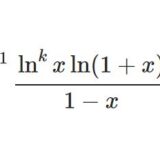
logを含む難しい積分17

logを含む難しい積分16
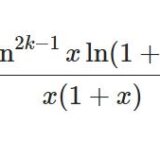
logを含む難しい積分15

三角関数の積・累乗を組み合わせた積分2

三角関数の積・累乗を組み合わせた積分

logを含む難しい積分14(調和数・重積分の応用)
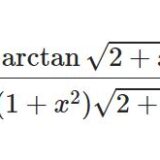
Ahmed's Integral
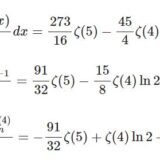
logを含む難しい積分13(Euler-sumの応用,weight5)
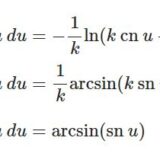
ヤコビの楕円関数を含む積分

ある4F3の特殊値と逆三角関数および対数正弦積分

楕円積分がみたす微分方程式とルジャンドルの関係式・singular value

Integrals and Miscellaneous 20

完全楕円積分と算術幾何平均・上昇/下降変換

楕円積分の導入とその計算方法2(ルジャンドル・ヤコビの標準形)

楕円積分の導入とその計算方法1

二重のlogを含む積分2(複素解析・偏角に注意!)

Integrals and Miscellaneous 19

Frullani積分とRamanujanによる一般化

Ramanujan's Master Theoremの留数定理による導出

Integrals and Miscellaneous 18

logを含む難しい積分12(超幾何関数の微分の応用)

Integrals and Miscellaneous 17

logを含む難しい積分11(調和数とEuler sumの利用)

logを含む難しい積分10(調和数・アーベルの級数変形法)

Integrals and Miscellaneous 16

logを含む難しい積分9

Integrals and Miscellaneous 15

ポリログを含む積分2(重積分・級数展開)

ポリログを含む積分1(重積分・級数展開)

Integrals and Miscellaneous 14

複2次式の平方根を含む積分(楕円積分の応用)

Integrals and Miscellaneous 13

双曲線関数を含む難しい積分1

二重のlogを含む積分1(ゼータ関数の微分)

logを含む難しい積分8

Integrals and Miscellaneous 12

複素積分演習(真性特異点)

複素積分演習(logの分岐点と切断)

logを含む難しい積分7(arcsinhの利用)

Integrals and Miscellaneous 11

logを含む難しい積分6(4F3・楕円積分・二重対数関数)

logを含む難しい積分5(超幾何級数3F2)

logを含む難しい積分4(複素積分演習)

logを含む難しい積分3(超幾何級数)

logを含む難しい積分2(級数展開)

logを含む難しい積分(調和数の4倍添え字を応用)

Integrals and Miscellaneous 10

複素積分演習(対数と2つの分岐点)

log(sinh x)の対数正弦積分(調和数・ポリログ)
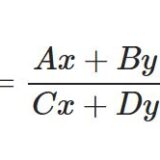
y'=(Ax+By+E)/(Cx+Dy+F)の形の微分方程式

ポリトロープとレーン・エムデン方程式
1階の同次形微分方程式(非線型)
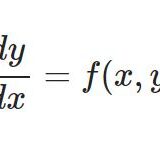
1階の非線型微分方程式 - 完全微分方程式・積分因子と具体例
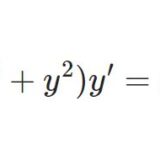
曲線の式から非線型微分方程式をつくる
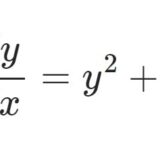
1階非線型微分方程式の例

フックス型とHeunの微分方程式

4個の確定特異点をもつフックス型微分方程式
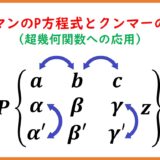
リーマンのP方程式と24個の特殊解

リーマンのP方程式とメビウス変換・超幾何関数

フックス型微分方程式とメビウス変換
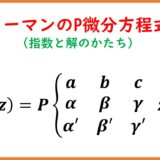
リーマンのP微分方程式の指数と解の関係

フックス型微分方程式と確定特異点2 (RiemannのP方程式)

フックス型微分方程式と確定特異点1(基本と例題)
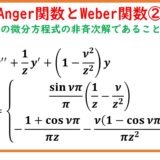
Anger関数とWeber関数②(ベッセル微分方程式の非斉次解)
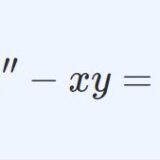
三角井戸型ポテンシャルとエアリー関数
【D20】球ベッセルの微分方程式
【D19】変形ベッセル微分方程式
【D18】ベッセルの微分方程式と級数解
【D17】超幾何微分方程式への変換例
偶奇統一!第1種ルジャンドル関数
【D16】Whittakerの微分方程式
【D15】合流型超幾何微分方程式とフロベニウス法
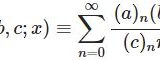
【D14】超幾何微分方程式とフロベニウス法・超幾何関数
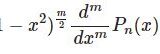
【D13】ルジャンドルの陪微分方程式
【D12】ルジャンドルの微分方程式
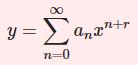
【D11】級数法・フロベニウス法
【D10】高階線型微分方程式の指針と例題
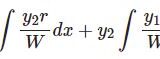
【D9】非斉次2階線型微分方程式その2
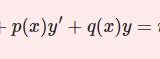
【D8】非斉次2階線型微分方程式その1
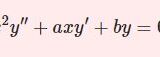
【D7】オイラー・コーシーの方程式
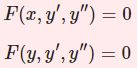
【D6】$y$または$x$を含まない2階方程式(階数低減法)
【D5】斉次2階線型微分方程式

【D4】Chrystalの微分方程式と包絡線
【D3】クレローの方程式と包絡線(解法と例題)
【D2】ベルヌーイの微分方程式
【D1】1階線型微分方程式の解法
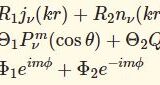
球座標系のヘルムホルツ方程式と球ベッセル関数
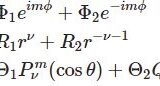
球座標のラプラス方程式とルジャンドル陪微分方程式
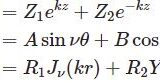
【物理数学】円筒座標のラプラス方程式とベッセル関数
【物理数学】N次元グリーン関数の解法(2)
【物理数学】N次元グリーン関数の解法(1)

シュトルツ・チェザロの定理(数列の極限)

数列の上極限と下極限
【ε論法】極限の計算:limをεδに
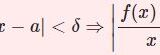
【ε論法】ε-δ論法によって微分する・例題7つ
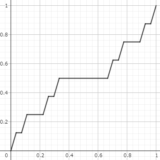
【ε論法】カントール集合と悪魔の階段の連続性
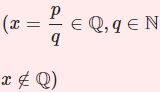
【ε論法】トマエ関数は有理数の点では不連続

【ε論法】連続関数の和も積も合成も連続関数
【ε論法】一様コーシーな関数列と一様収束性
【ε論法】関数列が一様収束でないことの証明
【ε論法】関数列の各点収束と一様収束
【ε論法】一様連続でないことの証明
【ε論法】関数の一様連続性の証明
【ε論法】関数の連続性とδのテクニック
【ε論法】コーシー列でないことの証明
【ε論法】数列がコーシー列であることの証明および収束性
【ε論法】数列の収束と極限・例題 ~εとNを使って~
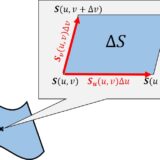
管状近傍とホテリングの定理・曲面の近傍とワイルの定理

曲面の面積とガウス写像の面積(ガウス曲率のもつ意味)
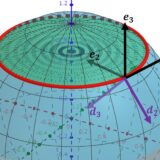
ダルブーフレームと測地的曲率・捩率・法曲率

曲率に関する「驚異の定理」と可展面
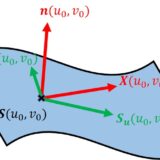
ガウスの公式とワインガルテンの公式

曲面の曲がり具合② ~主曲率とガウス曲率~

曲面の曲がり具合 ~法曲率~

曲面の第1基本形式と第2基本形式

空間内の曲面:パラメータ表示、接平面、法ベクトル、ガウス写像、面積
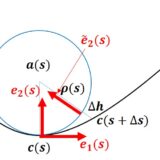
空間曲線2-接線・法線、接触平面・接触球
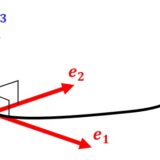
空間曲線1-弧長パラメータと動標構、曲率・捩率、フレネ・セレの公式
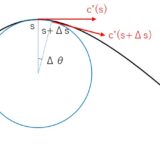
弧長パラメータと動標構、曲率、フレネ・セレの公式【平面曲線】
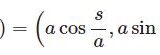
弧長パラメータ表示の導出と例題、そして難点
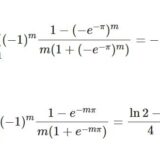
ヤコビの楕円関数5~無限積表示と対数のフーリエ展開

ヤコビの楕円関数4~周期を変換する・ペー関数との関係

テータ関数11~ヤコビの楕円関数の登場
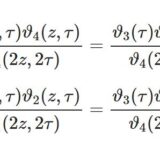
テータ関数10~ランデン変換と微分方程式
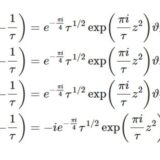
テータ関数9~ヤコビの虚数変換式
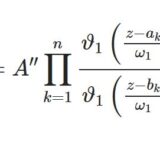
テータ関数8~ワイエルシュトラスのシグマ・ゼータ関数や楕円関数との関係
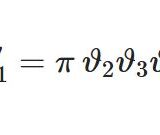
テータ関数7~無限積の導関数とテータ定数
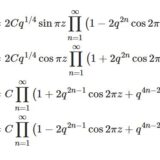
テータ関数6~無限積による表示

テータ関数5~ヤコビの基本関係式②

テータ関数4~ヤコビの基本関係式①
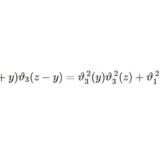
テータ関数3~周期性と極に注目した加法定理の導出
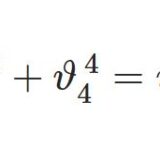
テータ関数2~零点・2乗の関係
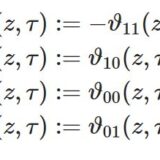
テータ関数1~定義と性質
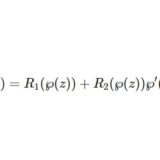
ワイエルシュトラスのペー関数8~任意の楕円関数をワイエルシュトラスの関数であらわす
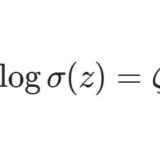
ワイエルシュトラスのペー関数7~シグマ関数:擬周期性をもつ整関数
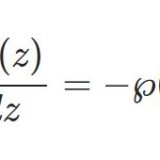
ワイエルシュトラスのペー関数6~擬周期性をもつゼータ関数
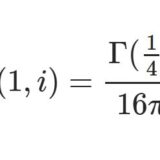
ワイエルシュトラスのペー関数5~周期・不変量・アイゼンシュタイン級数の計算

ワイエルシュトラスのペー関数4~三次方程式との関係・半周期
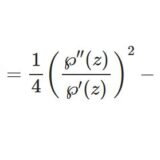
ワイエルシュトラスのペー関数3~同次性・加法定理等
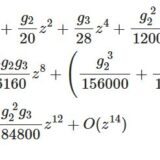
ワイエルシュトラスのペー関数2~係数の漸化式,積分公式
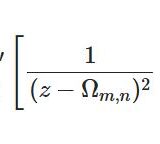
ワイエルシュトラスのペー関数1~基本的性質と級数展開
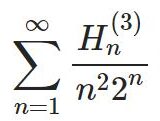
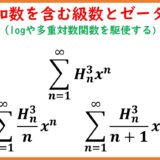
調和数を含んだ級数(Euler-sum)とゼータ関数 part17

logを含む難しい積分16
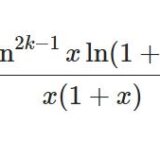
logを含む難しい積分15
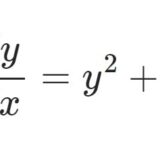
1階非線型微分方程式の例
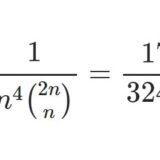
二項係数の逆数を含む級数
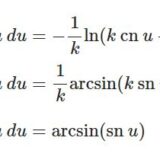
ヤコビの楕円関数を含む積分

ヤコビの楕円関数3(二重周期性・零点・極)

ある4F3の特殊値と逆三角関数および対数正弦積分

ヤコビの楕円関数2(定義域の拡張・半角公式・倍角公式・展開)

ヤコビの楕円関数(定義・導関数・加法定理)

楕円積分がみたす微分方程式とルジャンドルの関係式・singular value

完全楕円積分と算術幾何平均・上昇/下降変換

楕円積分の導入とその計算方法2(ルジャンドル・ヤコビの標準形)

楕円積分の導入とその計算方法1

【13】素数が無限積と級数をつなぐ(完全乗法的関数)

【12】無限積とガンマ関数

ハイパー階乗・K関数とGlaisher-Kinkelin定数②

ハイパー階乗・K関数とGlaisher-Kinkelin定数①
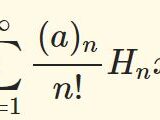
調和数と超幾何級数3

Integrals and Miscellaneous 18

logを含む難しい積分12(超幾何関数の微分の応用)

調和数を含んだ級数(Euler-sum)とゼータ関数 part16

logを含む難しい積分11(調和数とEuler sumの利用)

超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値3

超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値2

超幾何関数のパラメータによる微分とディガンマ関数、一般化超幾何関数の特殊値1
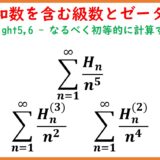
調和数を含んだ級数(Euler-sum)とゼータ関数 part14

Integrals and Miscellaneous 16
調和数を含んだ級数(Euler-sum)とゼータ関数 part13

音のうなり

大気圧と水圧の体感実習

孔雀石を塩酸につけたり加熱しよう

RC回路で充電しよう

浮沈子をつくる(浮力の実験)

自由落下による g の測定
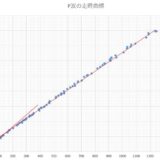
モホロビチッチ不連続面の深さを計算しよう

グラフを描いて海水の層構造を知ろう

音の干渉

音速の測定

発光ダイオードの電流電圧特性を調べよう

全波整流回路をつくろう

波の独立性や重ね合わせを確認しよう

波を起こしてパラメータに慣れよう

ペットボトルで雲をつくろう
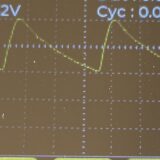
半波整流回路をつくろう

ペットボトルで漣痕(リップルマーク)を再現しよう

化石クイズをしよう

ブラウン運動を見よう

タービダイトと砂岩泥岩互層を再現しよう

二重スリットで光の干渉縞をみよう

コンデンサーの直列・並列回路の電圧を測定しよう

階段を駆け上がったときの仕事・仕事率は?

コンデンサーに電気をためよう

光の道筋を見よう!レンズによる屈折と反射

あなたの肩力は? 斜方投射と初速度・最高到達点

10m走で速度・加速度を計ろう

音叉は不要!スマホでドップラー効果

あなたの接地圧は? 足形をとってみよう!

紙コップで体重を支える!? 圧力の導入実験

簡易真空容器を使った減圧実験(膨張・沸点降下)

浮力の測定と密度・体積の計算

簡単実験!最大静止摩擦力の測定
- ヤコビの楕円関数5~無限積表示と対数のフーリエ展開楕円関数シリーズ第26回です。前回は: ヤコビの楕円関数をテータ関数で定義しました。過去にテータ関数の無限積表示を得ていますので、それを使えばヤコビの楕円関数の無限積表示も導出できそうで ...
- 音のうなり若干周波数の異なる音を発生させます。音叉を使ってもいいですが、スマホでアプリやWebを使って好きな周波数の音を出すことができます。もちろん2台必要です。 webの例:https://on ...
- ヤコビの楕円関数4~周期を変換する・ペー関数との関係テータ関数の周期τを変換することによって、ヤコビの楕円関数やそれにまつわるパラメータがどのように変化するかを考察する。またヤコビの楕円関数とペー関数の関係も導出する。
- テータ関数11~ヤコビの楕円関数の登場本記事は楕円関数シリーズの第24回となります: 前回は: ヤコビの楕円関数を楕円積分の逆関数として定義した記事を過去に書いています。読まなくても今回は大丈夫ですが、参考までに: 前回得た ...
- 大気圧と水圧の体感実習水槽に水を貯めます。100均とかに売っている使い捨てのポリ手袋を手に装着して、水槽中に手を突っ込むと、水圧で手袋がピタッと張り付いてきます。 次に手袋に水をいっぱいいれてから同じことをし ...
- テータ関数10~ランデン変換と微分方程式前回は: 本シリーズ一覧は: 最初に便利な擬周期、半周期の式を復習しておきます。 さてさて、\begin{equation}f(z):=\frac{\vartheta_3(z,\tau) ...
- テータ関数9~ヤコビの虚数変換式テータ関数の周期τを変換する公式である、ヤコビの虚数変換式を複素解析の方法で導出する。
- 初等整数問題①~下1桁の考察Ellina Grigorieva, "Methods of Solving Number Theory Problems"という本にあった問題を少しだけ深掘りします。もともとの問題はこ ...
- テータ関数8~ワイエルシュトラスのシグマ・ゼータ関数や楕円関数との関係テータ関数を楕円関数とつなげましょう。まずは無限積表示に注目してワイエルシュトラスのゼータ関数やシグマ関数との関係を導きます。
- 孔雀石を塩酸につけたり加熱しよう天然に存在する銅の鉱物である孔雀石の理想化学組成はCu2CO3(OH)2です。購入するか、銅の二次鉱物がとれる鉱山跡にいって入手しましょう。私は鉱山跡で採集しました。 孔雀石を小さく割っ ...
- テータ関数7~無限積の導関数とテータ定数前回に得たテータ関数の無限積表示を微分して導関数を導く。またそれと関連したテータ定数を用いて面白い関係式を導出しよう。
- テータ関数6~無限積による表示4つのテータ関数とテータ定数の無限積による表示を導出する。これまでに幾度も出現した複素解析による方法である。
- テータ関数5~ヤコビの基本関係式②前回のヤコビの基本関係式をもう少し掘り下げて、たくさんの公式を得る方法を紹介する。これまで導出した公式の上位にあるものが見えてくる。
- テータ関数4~ヤコビの基本関係式①4つのテータ関数の間にはさまざまな関係式が存在する。これらの関係式の上位には一般的な5項間関係式が存在し、次々と演繹される。
- テータ関数3~周期性と極に注目した加法定理の導出テータ関数の第3回。テータ関数を組み合わせて楕円関数をつくり、極に着目して加法定理を導出する。得た公式の特殊化・一般化についても触れる。
- テータ関数2~零点・2乗の関係テータ関数の第2回。前回導いた基本性質を使って、4つのテータ関数の零点の個数や位置、テータ関数の間で成り立つ関係式を導く。
- テータ関数1~定義と性質楕円関数ではないが二重の擬周期をもつテータ関数を解説。4つのテータ関数の最も基本的な変換公式を導出する。
- ワイエルシュトラスのペー関数9~楕円積分との関係前回はこちら: 初等的には計算できないが $\wp(z)$ を使って表すことができる積分(楕円積分)$$\int_{x_0}^x\left(a_0t^4+4a_1t^3+6a_2t^2+ ...
- ワイエルシュトラスのペー関数8~任意の楕円関数をワイエルシュトラスの関数であらわす任意の楕円関数をワイエルシュトラスのペー関数、ゼータ関数、シグマ関数でそれぞれ表現できることを解説する。楕円関数は極や零点によって特徴づけられることが明確になる。
- 1次元井戸型ポテンシャルの定常状態と確率(係数と分布を求める例題)1個の粒子が1次元無限井戸型ポテンシャル$$V(x)=\begin{cases}0\quad & (0<x<a)\\+\infty &(\mathrm{els ...
- ワイエルシュトラスのペー関数7~シグマ関数:擬周期性をもつ整関数ワイエルシュトラスのゼータ関数の積分で定義されるシグマ関数は、楕円関数ではないものの擬周期性をもつ整関数である。今回はこの定義と簡単な性質を解説する。
- ワイエルシュトラスのペー関数6~擬周期性をもつゼータ関数ペー関数の積分で定義されるワイエルシュトラスのゼータ関数は、最早楕円関数ではないものの、擬周期性をもつ。今回はゼータ関数の定義と簡単な性質について広く見ていく。
- ワイエルシュトラスのペー関数5~周期・不変量・アイゼンシュタイン級数の計算ワイエルシュトラスのペー関数において、周期から不変量を、あるいはその逆を導く例を解説。難しい積分とガンマ関数が現れる。同時にアイゼンシュタイン級数の計算例も説明する。
- ワイエルシュトラスのペー関数4~三次方程式との関係・半周期ワイエルシュトラスのペー関数について。導関数の零点、半周期、3次方程式と不変量について解説。
- ワイエルシュトラスのペー関数3~同次性・加法定理等ワイエルシュトラスのペー関数のシュワルツ微分、同次性、加法定理について解説。楕円関数の極や零点に関する性質を応用しよう。
- ワイエルシュトラスのペー関数2~係数の漸化式,積分公式ペー関数の級数展開において、係数にアイゼンシュタイン級数が現れる。その漸化式を導こう。またペー関数を楕円積分の逆関数として表そう。
- ワイエルシュトラスのペー関数1~基本的性質と級数展開シンプルな楕円関数であるペー関数の基本を学ぶ。関数項級数の収束性や偶奇性、周期性、展開式(アイゼンシュタイン級数)について説明する。
- 楕円関数の定義と基本的性質二重周期性によって一般の楕円関数を定義し、零点や極に関する諸性質を確認しよう。偏角の原理もここで解説。
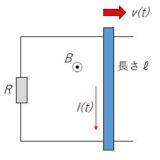
- RC回路で充電しよう高校物理の超簡単な実験シリーズ。コンデンサーは、その電気容量に応じて電気をためることができます。前回は単純に充電と放電をするだけでしたが、今回は充電中の電流値の変化や、充電した電気量を検 ...
- y'=(Ax+By+E)/(Cx+Dy+F)の形の微分方程式非線型微分方程式シリーズ。前回はこちら: \begin{equation}\frac{dy}{dx}=\frac{Ax+By+E}{Cx+Dy+F}\tag{0}\end{equatio ...
- ポリトロープとレーン・エムデン方程式球対称な密度分布をもつ流体の天体を考えます。例えば太陽のようなガスでできている恒星とか。恒星は中心の密度が一番高く、表面で密度ゼロです。 この星の内部で、半径 $r$ で厚さ $dr$ ...
- 浮沈子をつくる(浮力の実験)理科の超簡単な実験シリーズ。おうちでもできます。 準備物:醤油さし、M6ナット、炭酸のペットボトル 醤油さしは弁当に付属した魚型のものを使いましたが、最近は手に入るのでしょうか?100均 ...
- 調和数を含んだ級数(Euler-sum)とゼータ関数 part17シリーズ前回はこちら: ただし、本記事はむしろ次の記事のつづきという位置づけです: 今回はweight5のEuler-sumで、分母に $2^n$ が入っているもの$$\sum\frac ...
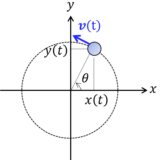
- logを含む難しい積分18(多重対数関数の積分ふくむ)前回はこちら: weight5の積分やEuler-sumを扱います。 はじめに$$\int_0^1\frac{\ln^3(1-x)\ln(1+x)}{x}dx$$を計算します。\begi ...
- logを含む難しい積分17結果にゼータ関数が現れるタイプの積分を紹介。Euler-sumとよばれるタイプの無限級数とも関連する。
- logを含む難しい積分16前回の続きです。前回はこちら。 前回の(15)式で\begin{equation}\int_0^\infty\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx=2\ ...
- logを含む難しい積分15前回は: 今回から、何回かに分けて、互いにつながりのあるいくつかの積分を計算していきます。過去記事とダブるものがあるかもしれませんが、掘り起こすのも面倒なので、一からやっていきます。 も ...
- 火砕岩中の輝沸石沸石類についてはあまり標本を見たことがなく、知らないことが多いのと、種類が多くて敬遠しているところです。今回は輝沸石のサンプルを手に入れましたので学んだことをばらばらと書いていきます。 ...
- 三角関数の積・累乗を組み合わせた積分2前回はこちら: やり方は前回と同様ですので、前回の記事を読まれた方は、本記事を読まずともできるかもしれません。 (1a)を示します。(1a)を $a_n$ と定義すると階差をとって\be ...
- 三角関数の積・累乗を組み合わせた積分本記事で扱う積分を次のように定義します。 積分の計算にはいくつかのアプローチがあります。 こちらで示した、$s>0$ で成り立つ等式\begin{equation}\int_0^\ ...
- logを含む難しい積分14(調和数・重積分の応用)前回は: 調和数がらみの級数シリーズはこちら: こちらの「2024/6/29」より $x\le 1$ に対して\begin{equation}\int_0^x\frac{t\ln(1-t ...
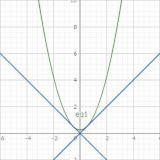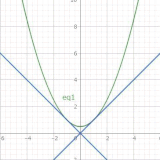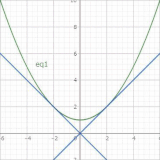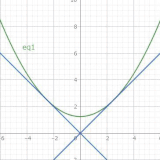
- 1階の同次形微分方程式(非線型)1階非線型微分方程式の同次形の場合の解法。積分因子によって完全方程式を得る方法をまず説明しますが、実践的には変数変換で簡単化する方法がありますので、そちらも紹介します。
- 自由落下による g の測定物理の超簡単な実験シリーズ。今回は重力加速度 $g$ を自由落下により測定します。等加速度直線運動を扱ったあと、その例として落体の運動を学びます。自由落下はそのもっとも単純な運動です。加 ...
- 1階の非線型微分方程式 - 完全微分方程式・積分因子と具体例非線型微分方程式シリーズです。前回はこちら; 今回は1階非線型微分方程式について。特に完全微分方程式によるアプローチと、それへの帰着のさせかたを解説します。 $x$ の関数 $y$ につ ...
- モホロビチッチ不連続面の深さを計算しよう地学の実習。 地殻とマントルの境界をモホロビチッチ不連続面(モホ面)とよびます。人類が最も深く掘った穴はコラ半島にある深さ12km程度のもので、地殻を突破できていません。つまり人類はマン ...
- 曲線の式から非線型微分方程式をつくる非線型微分方程式を解くのはもちろん難しい。ここでは逆に、解から方程式をつくり、非線型方程式の現れ方に馴染んでみよう。その形がいかに予測困難かを実感することも含めて。
- 1階非線型微分方程式の例$$\frac{dy}{dx}=y^2+x$$非線型微分方程式の有名なカテゴリ「Riccati型」の例題を解く。
- Ahmed's IntegralNahin [1] で紹介されている方法を解説します。1つ目の積分を$$I:=\int_0^1\frac{\arctan\sqrt{2+x^2}}{(1+x^2)\sqrt{2+x^2} ...
- グラフを描いて海水の層構造を知ろう地学の実習。 海は深くなるほど温度が下がります。1つのシンプルな理由としては太陽光を上層で受け、深いところには光が届かないからです。 参考資料[1]には深さと水温のデータがあります。これ ...
- logを含む難しい積分13(Euler-sumの応用,weight5)前回: $$I:=\int_0^1\frac{\ln^3x\ln(1-x)}{1+x}dx$$について、$\ln(1-x)$ と $\frac{1}{1+x}$ を級数展開します。$$I ...
- arcsinの累乗の級数展開と、二項係数・有限多重ゼータを含む級数について前回の記事からの延長です: 過去にすでに導出しましたが、Edwards[1] p74に載った別の方法を紹介します。$$y=f(x):=\arcsin^2x$$と定義すると$$y'=\fr ...
- 二項係数の逆数を含む級数@karenonaharaさんのツイートを見て、取り組んでみました。 分母に $n$ の4乗がありますが、本記事を読めばこれが $n^2$ , $n^3$ のときの値もすぐに分かります。 ...
- 音の干渉同じ音源を2つ用意します。昔ながらのものでは音叉がいいでしょう。スマホのアプリやwebブラウザを使って発音してもいいと思います。例:https://onlinetonegenerator ...
- 音速の測定高校物理の超簡単な実験シリーズ。音の速さを測定してみましょう。 準備物は音源とスマホくらいですが、必要なら50m程度のメジャーを用意します。音源は100m程度離れていても聞こえ、かつ10 ...
- 発光ダイオードの電流電圧特性を調べよう高校物理の実験シリーズ。発光ダイオード(LED)の特性を調べ、回路に応用しましょう。 準備物:赤色LED、抵抗220Ω、電流計と電圧計、可変電源等 すべて通販で買えます。抵抗はセットで買 ...
- 全波整流回路をつくろう高校物理の実験シリーズ。教科書の内容とは少し外れますが、ダイオードを使って整流してみましょう。 先にこちらで半波整流回路の知識を入れておきましょう: 準備物:以下で提示する回路を組む材料 ...
- ヤコビの楕円関数を含む積分ヤコビの楕円関数については: タイトルにある積分として最も簡単な積分をやってみましょう。まずは$$I_1 :=\int \sn u \:du$$$\sn u$ は母数も明示するなら $\ ...
- 緑色の鉱物を含む閃緑岩北海道で採集したものです。 色指数的には石英閃緑岩と思われます。写真では分かりませんが、やや緑がかっていたため、暗緑色の角閃石が豊富な石英閃緑岩かと思いましたが、そう単純ではないようです ...
- 花崗岩とアプライト関西石ころ旅。木津川で拾った2つのアプライトの紹介です。 アプライトは花崗岩質の岩体で見られる、優白質であり完晶質かつ比較的細粒なものをいいます[1]。簡単に言うと、有色鉱物が非常に少な ...
- 玄武岩中のレビ沸石長崎県平戸市で採集したものです。 ガラスが見られず完晶質斑状です。全体に細粒の輝石やかんらん石を石基として多く含んでいること(実体顕微鏡下で何となく判断しましたが、細粒の橄欖石と輝石は区 ...
- ヤコビの楕円関数3(二重周期性・零点・極)前回はヤコビの楕円関数3つを複素数へ拡張しました。複素関数となったからには、零点や極を知っておきたいところ。また、一般の楕円関数を定義づける二重周期性についても解説します。
- ある4F3の特殊値と逆三角関数および対数正弦積分Brychkov[1]の初等関数の定積分を眺めていると なる公式がありました。過去に得られた知見に基づけば、これの証明は難しくありません。 $\arccos x=\frac{\pi}{2 ...
- 波の独立性や重ね合わせを確認しよう高校物理の超簡単な実験シリーズ。ですが、ウェーブマシンを使用するので学校の先生向けかも。 ウェーブマシンの両端で波を起こします。山1つずつで十分です。このとき、波の大きさを異なるようにし ...
- 波を起こしてパラメータに慣れよう高校物理の超簡単な実験シリーズ。ですが、ウェーブマシンを使用するので学校の先生向けかも。ですが、何か波をつくれればOK。 まず波の基本的な要素を学習しておきます。横波の伝わる速さや波長、 ...
- ペットボトルで雲をつくろう地学分野の超簡単な実験シリーズ。今日は雲をつくってしまいましょう。 準備物:500mLペットボトル(炭酸飲料のもの)、炭酸を維持するキャップ、エタノール消毒液 2つ目のものは必ずしも必要 ...
- 半波整流回路をつくろう高校物理の実験シリーズ。教科書の内容とは少し外れますが、ダイオードを使って整流してみましょう。 準備物:以下で提示する回路を組む材料(ダイオード、DCモーター、電源トランス、オシロスコー ...
- ペットボトルで漣痕(リップルマーク)を再現しよう高校地学の超簡単な実習シリーズ。おうちでもできます。 地層の学習において、漣痕という言葉が出てきます。水流があると底の砂がなみなみの形になるものです。これをペットボトルと砂を使って再現し ...
- 化石クイズをしよう高校地学(中学理科?)の超簡単な実習シリーズ。おうちでもできます。 化石標本(化石標本12種) /3-654-03 もっと安いのも出回っていますので、適当に買いましょう(自分で発掘しても ...
- ブラウン運動を見よう高校物理の超簡単な実験シリーズ。ブラウン運動を見てみましょう。 準備物:光学顕微鏡(600倍以上)、スライドガラス、カバーガラス、ウスターソースまたは牛乳 当方、光学顕微鏡600倍で確認 ...
- 角閃石岩超塩基性の深成岩のうち、有色鉱物がほとんど角閃石であるものを角閃石岩(Hornblendite)といいます。マグマ内で晶出した角閃石がマグマだまりの底に沈殿してできたものです。斜長石が晶 ...
- タービダイトと砂岩泥岩互層を再現しよう高校地学の超簡単な実験シリーズ。おうちでもできます。 準備物:スプーン1つ、コップ等の容器1つ、泥、砂、透明な細長い容器 透明な細長い容器については、本記事ではメスシリンダーを使いました ...
- 流紋岩質溶結凝灰岩(室生火砕流)関西石ころ旅。京都府木津川市の木津川で採れた転石の紹介です。 全体的に黒い岩石です。上写真で、一定の方向に黒い模様が入っているのが分かるでしょうか。これは軽石が熱で溶けて引き延ばされなが ...
- 二重スリットで光の干渉縞をみよう高校物理の超簡単な実験シリーズ。おうちでもできます。レーザー光を二重スリットに通して干渉縞をつくりましょう。
- コンデンサーの直列・並列回路の電圧を測定しよう高校物理の超簡単な実験シリーズ。コンデンサー2つを直列または並列につなぎ、それぞれのコンデンサーにかかる電圧を測定します。これにより、教科書の理論との一致を確認できます。
- ヤコビの楕円関数2(定義域の拡張・半角公式・倍角公式・展開)3つのヤコビの楕円関数の定義域を、周期性や加法定理に注目して複素数全体にまで拡張します。さらに半角の公式や倍角の公式を導出し、三角関数や双曲線関数との類似性を確認します。
- 階段を駆け上がったときの仕事・仕事率は?高校物理の超簡単な実験シリーズ。仕事や仕事率を求める実験はいろいろありますが、台車などの実験器具を使わずとも、自分の体でやればいいのではないでしょうか。軽く運動することで、した仕事すなわ ...
- コンデンサーに電気をためよう高校物理の超簡単な実験シリーズ。コンデンサーは、その性能に応じて電気をためることができます。実際に貯まっていることを確かめてみましょう。
- 光の道筋を見よう!レンズによる屈折と反射高校物理の超簡単な実験シリーズ。安価な道具で、光が屈折や反射していく道筋を見てみましょう。
- ヤコビの楕円関数(定義・導関数・加法定理)楕円関数の初歩。「ヤコビの楕円関数」という特別なものから導入します。ヤコビの楕円関数は、三角関数と類似の性質をもつので親しみやすいです。
- あなたの肩力は? 斜方投射と初速度・最高到達点高校物理の超簡単な実験シリーズ。今回は斜方投射の学びを深める実験です。
- 10m走で速度・加速度を計ろう高校物理の超簡単な実験シリーズ。高校物理のはじめに勉強する速度と加速度。速度はともかく加速度はひとつの鬼門です。このあたりの話では、「1秒当たり」というのがカギになります。かかる時間を1 ...
- 音叉は不要!スマホでドップラー効果高校物理の超簡単な実験シリーズ。今回はドップラー効果を体感する実習を紹介します。ドップラー音叉は高級品で、買うなんてとんでもない…という方には、スマホで完結するのでオススメです。
- あなたの接地圧は? 足形をとってみよう!高校物理の超簡単な実験シリーズ。あなたが立っているとき、地面にどれくらいの圧力をかけているのでしょう?
- 紙コップで体重を支える!? 圧力の導入実験高校物理の超簡単な実験シリーズ。大きな面積で支えると、重いものでもつぶれません。圧力のお話。
- 楕円積分がみたす微分方程式とルジャンドルの関係式・singular value第1種完全楕円積分と第2種完全楕円積分が満たすルジャンドルの関係式を導出します。その際、これらの楕円積分が満たす微分方程式を利用します。またsingular valueについても解説。
- 簡易真空容器を使った減圧実験(膨張・沸点降下)高校物理の超簡単な実験シリーズ。今回は簡易真空容器を使って減圧することによる面白い現象を観察します。
- 浮力の測定と密度・体積の計算高校物理の超簡単な実験シリーズ。今回は浮力の測定および物体の密度や体積の計算です。
- 簡単実験!最大静止摩擦力の測定高校物理の超簡単な実験シリーズ。今回は最大静止摩擦力の測定です。
- Integrals and Miscellaneous 20.
- 完全楕円積分と算術幾何平均・上昇/下降変換第1種および第2種完全楕円積分と算術幾何平均の関係からスタートし、それを用いて上昇変換と下降変換を導出します。導関数や級数展開についても紹介。
- 楕円積分の導入とその計算方法2(ルジャンドル・ヤコビの標準形)楕円積分はすべて、初等関数と第1,2,3種楕円積分の線型結合で書かれる(ルジャンドル・ヤコビの標準形)ことを示す。
- 楕円積分の導入とその計算方法1有理関数中に4次多項式の無理函数があるものは、一般的に初等関数の範囲では積分できません。一見、無数のパターンがあってどうにもならなそうなこの積分は、実は数パターンに分類できて、その先に面白い世界が広がっています。
- 【17】オイラーの五角数定理とワトソンの五重積(ヤコビ三重積から得られる公式たち)$$\prod_{n=1}^\infty(1-z^{n})=\sum_{n=-\infty}^\infty(-1)^nz^{\frac{n(3n-1)}{2}}$$無限積の理論シリーズ第17回。ヤコビの三重積から得られるオイラーの五角数定理、ガウスの三角数定理、ワトソンの五重積などを解説。
- 【16】ヤコビの三重積$$\prod_{n=0}^\infty(1-q^{2n+2})(1+zq^{2n+1})\left(1+\frac{q^{2n+1}}{z}\right)=\sum_{n=-\infty}^\infty q^{n^2}z^n$$無限積の理論シリーズ第16回。少し複雑な無限積の級数展開からはじめ、有名なヤコビの三重積へと至ります。
- 【15】自然数の分割と無限積の展開式2$$\prod_{n\in\mathcal{A}}\frac{1}{1+z^{n}}=1+\sum_{m=1}^\infty \{A_e(m;\mathcal{A})-A_o(m;\mathcal{A})\}z^m$$無限積の理論シリーズ第15回。4種類の無限積を級数展開して、無限積が分割の個数の母関数になることを解説。その応用として「オイラーの分割恒等式」を紹介。
- 【14】自然数の分割と無限積の展開式$$\prod_{n=1}^\infty\frac{1}{1-z^n}=1+\sum_{m=1}^\infty p(m)z^m$$無限積の理論シリーズ第14回。今回も「無限積=級数」なる等式を考えますが、無限積をより直接的に級数展開します。すると無限積は分割数の母関数となるという面白い事実が!
- 【13】素数が無限積と級数をつなぐ(完全乗法的関数)$$\sum_{n=1}^\infty f(n)=\prod_{n=1}^\infty\frac{1}{1-f(p_n)}$$無限積の理論シリーズ第13回。ゼータ関数の無限積表示を手掛かりに、完全乗法的関数を用いて一般化し、素数が無限積と級数をつなぐ役割を果たすことを見ていきます。
- 【12】無限積とガンマ関数$$\lim_{n\to\infty}\frac{n^zn!}{\prod_{j=0}^n(z+j)}$$無限積の理論シリーズ第12回。今回はガンマ関数の無限積による定義を確認します。ワイエルシュトラスの因数分解定理の視点からも見られます。その定義が、知られたガンマ関数の性質と一致することも見ましょう。
- 【11】二重無限積$$\prod_{m=1}^\infty\prod_{n=1}^\infty z_{mn}$$無限積の理論シリーズ第11回。今回は二重無限積の収束と順序について、例を交えて解説します。
- ハイパー階乗・K関数とGlaisher-Kinkelin定数②$$A=\lim_{n\to\infty}\frac{H(n)\:e^{\frac{n^2}{4}}}{n^{\frac{n^2}{2}+\frac{n}{2}+\frac{1}{12}}}$$K関数の特殊値や対数K関数の積分について、Glaisher-Kinkelin定数のさまざまな表示について説明します。