$xy$ 平面上の図形とその方程式を考えます。例えば半径$2$の円であれば\begin{equation}x^2+y^2=4\end{equation}のように $x,y$ の関係式として表示することができます。あるいは媒介変数を用いることで\begin{equation}\begin{cases}x&=& 2\cos\theta\\y&=& 2\sin\theta\end{cases}\end{equation}とすることもできます。
媒介変数で同じ円を表すには、ほかにも\begin{equation}\begin{cases}x&=& 2\cos2\theta\\y&=& 2\sin2\theta\end{cases}\end{equation}\begin{equation}\begin{cases}x&=& 2\cos e^{3\theta}\\y&=& 2\sin e^{3\theta}\end{cases}\end{equation}でもいいです(始点終点を統一するなら $\theta$ の範囲を変える必要はあります)。このように媒介変数の取り方は無数に考えられるのですが、とりわけ何か便利な表示はないだろうかと思うわけです。その1つが「弧長パラメータ表示」です。この表示にはメリット・デメリットあります。
半径$2$の円の弧長パラメータ表示は、弧長パラメータ $s$ を用いて\begin{equation}\begin{cases}x(s)&=& 2\cos\displaystyle\frac{s}{2}\\y(s)&=& 2\sin\displaystyle\frac{s}{2}\end{cases}\end{equation}となります。より一般には以下の事実があります。
\begin{equation}\begin{cases}x(s)&=& a\cos\displaystyle\frac{s}{a}\\y(s)&=& a\sin\displaystyle\frac{s}{a}\end{cases}\end{equation}
そもそもこの弧長パラメータ表示とは何なのでしょうか。この円を一周することを考えてみましょう。半径 $a$ であれば一周する弧長は $2\pi a$ です。そこで $s=2\pi a$ を上式に代入してみると\begin{equation}\begin{cases}x(2\pi a)&=& a\\y(2\pi a)&=& 0\end{cases}\end{equation}これが示す点 $(a,0)$ は円をちょうど一周して帰ってきた点です。あるいは半周なら\begin{equation}\begin{cases}x(\pi a)&=& -a\\y(\pi a)&=& 0\end{cases}\end{equation}これは円をちょうど半周した点です。つまり弧長パラメータを使うと、点 $(x(0),y(0))$ からスタートして、弧長が $s$ となるときの点が $(x(s),y(s))$ である、ということになりますね。弧長パラメータ表示は弧長が $s$ であるときの座標が一目で分かるというメリットがあります。
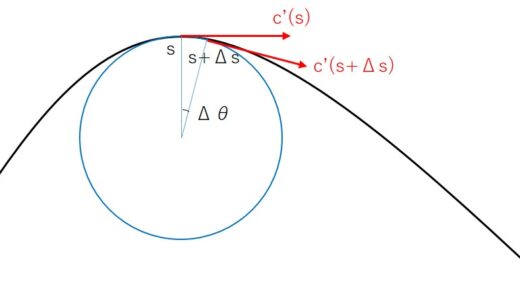
高等学校でも学ぶように、適当な媒介変数 $t$ を $0$ から $t$ まで変化させたときの弧長は\begin{equation}s(t)=\int_0^t\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\end{equation}と表すことができます。媒介変数を弧長パラメータ $s$ にすれば、先ほどの話から $s$ を $0$ から $s$ まで変化させたときの弧長は $s$ なのですから\begin{equation}s=\int_0^s\sqrt{\left(\frac{dx}{ds}\right)^2+\left(\frac{dy}{ds}\right)^2}ds\end{equation}左辺を移項すると\begin{equation}0=\int_0^s\left[\sqrt{\left(\frac{dx}{ds}\right)^2+\left(\frac{dy}{ds}\right)^2}-1\right]ds\end{equation}以上から\begin{equation}\therefore\;\sqrt{\left(\frac{dx}{ds}\right)^2+\left(\frac{dy}{ds}\right)^2}=1\tag{1}\end{equation}が常に成立します。つまり $x(s),y(s)$ を微分して得られる接ベクトル $(x'(s),y'(s))$ は常に単位ベクトルであるということになります。
この式が長ったらしいので今後は $c(s)=(x(s),y(s))$ , $c'(s)=(x'(s),y'(s))$などと書き、\begin{equation}|c'(s)|=\sqrt{\left(\frac{dx}{ds}\right)^2+\left(\frac{dy}{ds}\right)^2}\end{equation}と書くことにします。すると式(1)は\begin{equation}|c'(s)|=1\end{equation}というふうに書けます。
<基本チェック>
$c(t)\equiv\left(4\cos\displaystyle\frac{t}{4},4\sin\displaystyle\frac{t}{4}\right)$ を微分して接ベクトルの大きさ $|c'(t)|$ を求め、$t$ が弧長パラメータであることを示せ。
先ほど示した円の弧長パラメータ表示をどのように導出するのでしょうか?とりあえず、よくある円の媒介変数表示$c(t)=(a\cos t,a\sin t)$ と書きます。この書き方は確かに半径 $a$ の円ではありますが、弧長パラメータ表示にはなっていません。そこで $t$ を弧長 $s$ の関数 $t(s)$ と書ければ、$c(t(s))$ となって $s$ を媒介変数とした形となります。つまり、「適当な媒介変数 $t$ を弧長 $s$ の関数 $t(s)$ として表せば弧長パラメータ表示が得られる」ということになります。やってみましょう。
媒介変数 $t$ を用いると弧長 $s$ は
\begin{eqnarray}s&=&\int_0^t\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\\&=&\int_0^ta\sqrt{(-\sin t)^2+(\cos t)^2}dt\\&=&at\end{eqnarray}\begin{equation}\therefore\quad t(s)=\frac{s}{a}\end{equation}これで $t$ を $s$ の関数として表せました。あとはこの $t$ をもとの表示へ代入して\begin{equation}c(s)=\left(a\cos\displaystyle\frac{s}{a},a\sin\displaystyle\frac{s}{a}\right)\end{equation}これが円の弧長パラメータ表示です!
次に一般の曲線について考えてみます。まずは曲線を適当な媒介変数で表します。\begin{equation}c(t)=(x(t),y(t))\end{equation}$t=0\to t$ の弧長 $s$は\begin{equation}s(t)=\int_0^t\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt\end{equation}となります。右辺の積分を計算した上で、$s(t)$ の逆関数 $t(s)$ を求めます(これが不可能な場合が多いのが難点)。逆関数 $t(s)$ をさっきの媒介変数表示に代入すれば\begin{equation}c(t(s))=\bigl(x(t(s)),y(t(s))\bigr)\end{equation}これは $s$ の式ですから結局\begin{equation}c(s)=(x(s),y(s))\end{equation}と書けたことになります。この導出方法を使ってあとでいくつか例をやってみます。
話はそれますが、弧長パラメータ表示から比較的簡単に曲線の曲率を表すことができます。
\begin{equation}\kappa(s)\equiv |c^{\prime\prime}(s)|\end{equation}
弧長パラメータ表示を使うひとつのメリットです。これについては次回の記事で詳説しています。
弧長パラメータは接ベクトルを使いたいときなどに便利ですが、円の例を見ても分かるように、そのかわりに式がややこしくなることが多く、主たるデメリットとなっています。式がややこしいどころか、弧長パラメータ表示を導出するのは困難なことが多いです。そもそもうまく表せないんですよね。例えば、
二次関数 $y=x^2$ の弧長パラメータ表示を試みよ。
をやってみてください。
$c(t)=(t,t^2)$ とすると,$c^\prime (t)=(1,2t)$ なので弧長は\begin{eqnarray}s&=&\int_0^t \sqrt{1+4t^2}dt\\&=&\frac{t}{2}\sqrt{1+4t^2}+\frac{1}{4}\log (\sqrt{1+4t^2}+2t)\end{eqnarray}
この逆関数 $t(s)$ を求めることができればいいのですが、無理っぽいですよね。最初の $c(t)=(t,t^2)$ という表示をもっとうまくやればどうにかなるのか分かりませんが、とにかく弧長パラメータというのはそう簡単なものではないことが分かります。
$r=\theta$ $(\t\ge 0)$ の弧長パラメータ表示を試みよ。
$c(t)=(t\cos t,t\sin t)$ とすると,$$c^\prime (t)=(\cos t-t\sin t,\sin t+t\cos t)$$ なので弧長は\begin{eqnarray}s&=&\int_0^t \sqrt{1+t^2}dt\\&=&\frac{t}{2}\sqrt{1+t^2}+\frac{1}{2}\log (\sqrt{1+t^2}+t)\end{eqnarray}例題1aと同じで無理そうです.
直線 $y=2x+1\;(x\ge 0)$ について、
(1) 弧長パラメータで表示せよ。
(2) 接ベクトルの大きさ $|c'(s)|=1$ を確かめよ。
(3) $(0,1)$ からスタートして弧長が4となる点を求めよ。
(1)この直線は変数 $t$ を用いて\begin{equation}c(t)=(t,2t+1)\end{equation}
と表せます。$c'(t)=(1,2)$ より弧長 $s$ は\begin{equation}s=\int_0^t\sqrt{5}dt=\sqrt{5}t\end{equation}\begin{equation}\therefore\; t=\frac{s}{\sqrt{5}}\end{equation}$c(t)$ へ代入して\begin{equation}c(s)=\left(\frac{s}{\sqrt{5}},\frac{2}{\sqrt{5}}s+1\right)\end{equation}
(2) $c'(s)=(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}})$ より、その大きさは\begin{equation}|c'(s)|=\sqrt{\frac{1}{5}+\frac{4}{5}}=1\end{equation}
(3) $c(4)=(x(4),y(4))$\begin{equation}\therefore\; \left(\frac{4}{\sqrt{5}},\frac{8}{\sqrt{5}}+1\right)\end{equation}
図では以下のようになります。

$c(t)=(e^{-t}\cos t,e^{-t}\sin t)$の弧長パラメータ表示を求めよ.
まずは微分して\begin{equation}c'(t)=\Bigl(-e^{-t}(\cos t+\sin t),e^{-t}(\cos t-\sin t)\Bigr)\end{equation}この大きさは\begin{equation}|c'(t)|=\sqrt{2}e^{-t}\end{equation}よって弧長を $t$ で表すと\begin{equation}s=\int^t_0\sqrt{2}e^{-t}dt=\sqrt{2}(1-e^{-t})\end{equation}これを変形して\begin{equation}e^{-t}=1-\frac{s}{\sqrt{2}}\end{equation}および\begin{equation}t=-\log\left(1-\frac{s}{\sqrt{2}}\right)\end{equation}これらをはじめの式に代入すれば\begin{equation}c(s)=\biggl(\Bigl(1-\frac{s}{\sqrt{2}}\Bigr)\cos \log \Bigl(1-\frac{s}{\sqrt{2}}\Bigr),-\Bigl(1-\frac{s}{\sqrt{2}}\Bigr)\sin \log \Bigl(1-\frac{s}{\sqrt{2}}\Bigr)\biggr)\end{equation}うーん、やはり弧長パラメータ表示は複雑な式になりますね。
$c(t)=(t,\cosh t)$ の弧長パラメータ表示を求めよ.$|c'(s)|=1$を確認し,曲率 $\kappa(s)$ を求めよ.
微分して絶対値をとると\begin{equation}|c'(t)|=\sqrt{1+\sinh^2t}=\cosh t\end{equation}よって弧長は\begin{equation}s=\int^t_0\cosh tdt=\sinh t\end{equation}$\sinh t$ を指数で表して変形していけば逆関数を求めることができて\begin{equation}t=\log(s+\sqrt{s^2+1})\end{equation}これで $x$ 座標を得られます。また $\cosh t=\sqrt{1+\sinh^2t}=\sqrt{1+s^2}$ から $y$ 座標も得られ、弧長パラメータ表示 $c(s)$ は\begin{equation}\begin{cases}x(s)&=&\log(s+\sqrt{s^2+1})\\y(s)&=&\sqrt{s^2+1}\end{cases}\end{equation}と求まりました。
次に $c'(s)$ を計算します。ここまで計算したことを活かすと早くできます。$x=t$ なので\begin{eqnarray*}\frac{dx}{ds}&=&\frac{dt}{ds}\\&=&\left(\frac{ds}{dt}\right)^{-1}\\&=&\left(\frac{d}{dt}\sinh t\right)^{-1}\\&=&\frac{1}{\cosh t}\\&=&\frac{1}{\sqrt{1+s^2}}\end{eqnarray*}一方 $y=\cosh t$ のほうは\begin{eqnarray*}\frac{dy}{ds}&=&\frac{dy}{dt}\frac{dt}{ds}\\&=&\sinh t\frac{1}{\sqrt{1+s^2}}\\&=&\frac{s}{\sqrt{1+s^2}}\end{eqnarray*}\begin{equation}\therefore\; c'(s)=\left(\frac{1}{\sqrt{s^2+1}},\frac{s}{\sqrt{s^2+1}}\right)\end{equation}\begin{equation}\therefore\; |c'(s)|=1\end{equation}
曲率を求めるために再度微分します。\begin{equation}c^{\prime\prime}(s)=\left(-\frac{s}{(s^2+1)^{\frac{3}{2}}}\;,\;\frac{1}{(s^2+1)^{\frac{3}{2}}}\right)\end{equation}\begin{equation}\therefore \;\kappa(s)=|c^{\prime\prime} (s)|=\frac{1}{s^2+1}\end{equation}
$c(t)=(t-\sin t,1-\cos t)\;(0\le t\le 2\pi)$ の曲率を求めよ.
同様に計算していくと、弧長 $s$ は\begin{equation}s=4(1-\cos\frac{t}{2})\end{equation}よって弧長パラメータ表示は\begin{equation}c(s)=\left(2\arccos(1-\frac{s}{4})-\frac{4-s}{8}\sqrt{s(8-s)},s-\frac{s^2}{8} \right)\end{equation}微分して,\begin{equation}c^\prime(s)=\left(\frac{1}{4}\sqrt{8s-s^2},1-\frac{s}{4}\right)\end{equation}さらに微分して絶対値をとることで曲率は,\begin{equation}\kappa(s)=\frac{1}{\sqrt{s(8-s)}}\end{equation}となります。
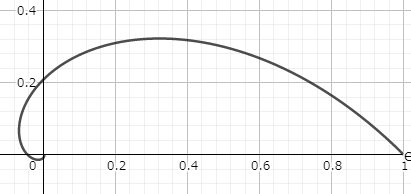
極方程式 $r=\t^2$ $(\t\ge 0)$ で表される曲線を媒介変数表示したのち,弧長パラメータ表示を求めよ.
外へ向かってだんだん間隔が広くなっていくうずまきです.媒介変数表示は $x=t^2\cos t$ , $y=t^2\sin t$ です.よって$$c'(t)=(2t\cos t-t^2\sin t,2t\sin t+t^2\cos t)$$$$\therefore\quad|c'(t)|=t\sqrt{4+t^2}$$$$s=\int_0^tt\sqrt{4+t^2}dt=\frac{1}{3}\left[(4+t^2)^\frac{3}{2}-8\right]$$逆に解くと$$t=\sqrt{(3s+8)^\frac{2}{3}-4}$$以上から弧長パラメータ表示は$$\begin{cases}x(s)&=&\left[(3s+8)^\frac{2}{3}-4\right]\cos\sqrt{(3s+8)^\frac{2}{3}-4}\\y(s)&=&\left[(3s+8)^\frac{2}{3}-4\right]\sin\sqrt{(3s+8)^\frac{2}{3}-4}\end{cases}$$
次回はこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。