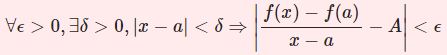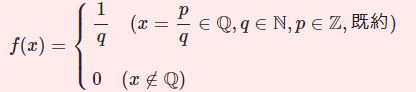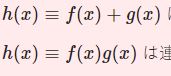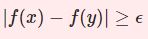関数列の収束について $\epsilon-N$ 論法を用いて説明していきます。関数列の収束には種類があり、ここでは「各点収束」「一様収束」の２つを取り上げます。「各点収束」は単に「収束」ともいいます。「一様収束」はもっと厳しい条件の収束です。例題とともに詳しく見ていきましょう。
定義域 $I$ の関数列 $\{f_n(x)\}$ が $n\to\infty$ で $f(x)$ へ各点収束する（あるいは単に収束する）とは以下を満たすことです。
任意の点 $a\in I$ に対して、任意の $\epsilon>0$ に対してある自然数 $N$ が存在し$$n>N\Longrightarrow|f_n(a)-f(a)|<\epsilon$$とできる。
「各点収束」では関数列 $f_n(x)$ の$x$ を $x=a$ と先に固定して、 $f_n(a)$ がある値に収束することを論じます。$f_n(a)$ は $f_n(a)=A_n$ のような形に書き換えればもはや関数列というよりはただの数列であり、結局は数列の収束を考えることに帰着します。上記は確かに数列の収束の定義と同じ形ですね。もちろん固定する値 $a$ は任意ですから、すべての点での収束性を説明したことにはなりますが、「各点がばらばらのペースで収束」というイメージです。先に $a$ が定まっていますから、$N$ は $a$ に依存しても構いません。
数列の収束については以前書いたので参考にしてください。
【ε論法】数列の収束と極限・例題 ～εとNを使って～
$x\in[0,1]$ で定義される関数列 $f_n(x)=x^n$ は $$f(x)=\begin{cases} 0 & (0\le x<1) \\ 1 & (x=1)\end{cases} $$ へ各点収束することを示せ．
$f_n(0)=0 , f_n(1)=1$ なので $x=0,1$ で収束することは自明です。なので残りの範囲 $0<x<1$ で収束するかを見極めます。
$x=a\in(0,1)$ と固定し$$|f_n(a)-f(a)|=a^n<a^N$$よって $a^N\le\epsilon$ となるように適当に $N$ をとればよいです。$a$ は$1$未満の数なので $N$ を十分に大きくとれば $a^N$ はどんな $\epsilon$ よりも小さく取れますね。結局は以下のようになります。
任意の $\epsilon>0$ に対して $N=\lceil\log_a\epsilon\rceil+1$ とすると、$n>N$ なるすべての $n$ について$$|f_n(a)-f(a)|=a^n\le a^N=a^{\lceil\log_a\epsilon\rceil+1}<a^{\log_a\epsilon}=\epsilon$$
この関数列 $f_n(x)=x^n$ は各点収束するのですが、$f_n(x)$ が連続関数なのに収束先の関数 $f(x)$ は連続ではありません。収束したはいいものの、まるで別の関数だなぁという感じですね・・・。こういった関数列は、積分などと合わせて出現した場合、極限操作の順番を入れ替えられないなどの問題を抱えることになります。実はこの関数列は各点収束するものの、一様収束はしません。一様収束する連続関数の列は、収束先も連続関数になりますし、極限操作の入れ替えができるなどうれしい性質を持つのです。
$x\in\mathbb{R}$ で定義される関数列 $f_n(x)=x/n$ は $f(x)=0$ へ各点収束する。
任意の $\epsilon>0$ に対して $N>\displaystyle\frac{|a|}{\epsilon}$ を満たす $N$ を適当に取ります。$$|f_n(x)-0|=\frac{|a|}{n}<\frac{|a|}{N}<\epsilon$$よって各点収束します。
任意の $\epsilon>0$ に対してある自然数 $N$ が存在し$$n> N\Longrightarrow |f_n(x)-f(x)|<\epsilon$$とできるとき、関数列 $\{f_n(x)\}$ は一様収束する。
「一様収束」はもっと厳しい収束の条件です。各点とは違い、簡単に言えば関数列がどの点でも同じようなペースで収束する、というイメージです。
各点収束のときはまず $x$ を固定していましたが、今回は違います。一様収束の特徴は「$n$ を十分大きくとればあらゆる $x$ について $f_n(x)$ と $f(x)$ の差が $0$ 」となることです。「え！各点収束のときだって $x$ は"任意に"固定していたじゃないか！」と思うかもしれませんが、各点収束のときは一番先に $x$ を固定していたという部分が違うのです。
各点収束では $x$ ごとに $N$ を定めてよかったですが、今回は $N$ を定めるのが先で、その結果任意の $x$ についてうんたらかんたらということです。ですので $N$ は $x$ に依存しません。
$f_n(x)=\displaystyle\frac{1}{x^2+n^2}\; \; (x\in\mathbb{R})$ は $f(x)=0$ へ一様収束する。
任意の $\epsilon>0$ に対し $N=\lceil 1/\epsilon\rceil+1$ ととると、$\forall n> N$ に対して$$|f_n(x)-0|=\frac{1}{x^2+n^2}\le\frac{1}{x^2+N^2}\le\frac{1}{N^2}\le\frac{1}{N}<\epsilon$$よって$f_n(x)$ は $0$ に一様収束します。
$N$ の見つけ方は $|f_n(x)-0|<\cdots<\cdots$ と評価していって、$N$ が現れたところで 最右辺$<\epsilon$ としてみればいいです。慣れが大事だと思います。
$f_n(x)=\displaystyle\frac{x^{2021}}{x^2+n^{34}}\; \; (x\in [0,1])$ は $f(x)=0$ へ一様収束する。
任意の $\epsilon>0$ に対し $N=\lceil 1/\epsilon\rceil+1$ ととると、$\forall n> N$ に対して$$|f_n(x)-0|=\frac{x^{2021}}{x^2+n^{34}}\le\frac{1}{x^2+n^{34}}\le\frac{1}{n^{34}}\le\frac{1}{N}<\epsilon$$よって $f_n(x)$ は$0$に一様収束します。
関数列 $f_n(x)=\sin nx$ の区間 $(0,\pi)$ について考える．
(1) 数列 $f_n(\pi/2)=\sin\frac{n\pi}{2}$ は収束するか．
(2) 関数列 $f_n(x)$ は区間 $(0,\pi)$ で収束するか．
区間を $[0,\pi]$ としてもよかったのですが，$x=0,\pi$ で収束することは自明なので $(0,\pi)$ としました．
(1) $\epsilon=1$ ととると $\forall N\in\mathbb{N}$ に対し $m=4N+1>N$ , $n=2N>N$ ととれば\begin{eqnarray*}\left|\sin\frac{m\pi}{2}-\sin\frac{n\pi}{2}\right| &=& \left|\sin\frac{(4N+1)\pi}{2}-\sin\frac{2N\pi}{2}\right|\\ &=& \left|\sin\frac{\pi}{2}-\sin N\pi\right|\\ &=& 1 \ge \epsilon\end{eqnarray*}これはコーシー列でないことを示しますから，収束しません．
(2) 背理法を用います。(1)で $x=\pi/2$ では収束しないことは分かっているので，それ以外の点で収束するか考察します．任意の点 $a\in (0,\pi) ,a\neq\pi/2$ をとります．$f_n(a)$ が収束すると仮定すると $a$ に応じて極限値 $A$ が存在します．つまり任意の $\epsilon$ に対し自然数 $N$ が存在し、$$\forall n>N\;,\; |f_{n-1}(x)-A|<\epsilon$$が成立します．事情があって添え字が $n-1$ となっていますが $N$ を $1$ 大きくとれば問題ありません．$n-1$ で上式が成り立つならそれより大きい $n$ や $n+1$ でも成り立ちますから\begin{equation}|\sin(n+1)a-A|<\epsilon\end{equation}\begin{equation}|\sin na-A|<\epsilon\end{equation}\begin{equation}|\sin(n-1)a-A|<\epsilon\end{equation}真ん中の式は今は放置して，1番目と3番目の式の絶対値をはずすと\begin{equation}A-\epsilon<\sin(n+1)a<A+\epsilon\end{equation}\begin{equation}A-\epsilon<\sin(n-1)a<A+\epsilon\end{equation}加法定理を使うことで以下の2式が得られます．\begin{equation}A-\epsilon<\sin na\cos a<A+\epsilon\end{equation}\begin{equation}-\epsilon<\cos na\sin a<\epsilon\end{equation}絶対値を用いると\begin{equation}|\sin na\cos a-A|<\epsilon\end{equation}\begin{equation}|\cos na\sin a|<\epsilon\end{equation}
以上から次の3式が同時に成立することになります．\begin{equation}|\sin na-A|<\epsilon\tag{1}\end{equation}\begin{equation}|\sin na\cos a-A|<\epsilon\tag{2}\end{equation}\begin{equation}|\cos na\sin a|<\epsilon\tag{3}\end{equation}$a\neq\pi/2$ より $\cos a\neq 0$ ですから，式(1)(2)は$$\lim_{n\to\infty}\sin na=A$$$$\lim_{n\to\infty}\sin na=\frac{A}{\cos a}$$であることを示します．よって $\cos a=1$ か $A=0$ となりますが，区間 $(0,\pi)$ で前者はありえないので $A=0$ です．
従って式(1)(3)および $\sin a\neq 0$ から$$|\sin na|<\epsilon$$$$|\cos na|<\frac{\epsilon}{|\sin a|}$$$2$乗して足すと$$1<\epsilon^2\left(1+\frac{1}{\sin^2 a}\right)$$これは $\epsilon>0$ が任意であることに反し矛盾です．したがって関数列は各点収束しません．
さて、証明方法や定義は分かったものの、ただの（各点）収束と一様収束は結果として何が違うのでしょうか？次回の記事
では一様収束しないことの証明について解説し、一様収束しないことによって何が起こるのか、一様収束だと何が嬉しいのかを論じていきたいと思います。
$\epsilon$ 論法は慣れるまでは難しいですが、数列の収束、コーシー列、連続性、一様連続性、関数列の収束・・・などと取り組んでいる間にだんだん分かってきます。$\epsilon$ 論法を使った記事をさまざま書いてますので、読んでみてください。
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。