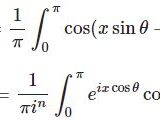$$I=\int_0^{2\pi}\frac{dx}{3+2\sin x}$$をワイエルシュトラス置換により求める.
決してエレガントな解法ではないですが、泥臭くも威力のある方法について紹介します。
$$\int_0^{2\pi} R(\cos x,\sin x)dx$$において $\tan\displaystyle\frac{x}{2}=t$ とおくと$$\cos x=\frac{1-t^2}{1+t^2} \;,\; \sin x =\frac{2t}{1+t^2}$$$$dx=\frac{2dt}{1+t^2}$$より
$$\int_{0}^{2\pi}R(\cos x,\sin x)dx=\int^\infty_{-\infty}R\left( \frac{1-t^2}{1+t^2},\frac{2t}{1+t^2} \right)\frac{2dt}{1+t^2}$$
と変形できます。ここからも面倒な計算になることが多いですが、ごり押しで解けたりします。なお、積分範囲について補足すると、\begin{eqnarray}\int_0^{2\pi}dx&=&\int_0^\pi dx+\int_\pi^{2\pi}dx\\&=& \int_0^\infty dt+\int_{-\infty}^0dt\\&=&\int^\infty_{-\infty}dt\end{eqnarray}というわけです。
積分範囲にはバリエーションありますので都度適切にやってください。
では$$I=\int_0^{2\pi}\frac{dx}{3+2\sin x}$$ を計算しましょう。ワイエルシュトラス置換により、\begin{eqnarray}I&=&\int^\infty_{-\infty}\frac{1}{3+2\frac{2t}{1+t^2}}\frac{2dt}{1+t^2}\\&=& \int^\infty_{-\infty}\frac{2dt}{3t^2+4t+3}\\&=& \int^\infty_{-\infty}\frac{2dt}{3(t+\frac{2}{3})^2+\frac{5}{3}}\\&=& \int^\infty_{-\infty}\frac{2dt}{3t^2+\frac{5}{3}}\\&=& \frac{2}{3}\int^\infty_{-\infty}\frac{dt}{t^2+\frac{5}{9}}\\&=& \frac{2}{3}\int^\infty_{-\infty}\frac{\frac{\sqrt{5}}{3}dy}{\frac{5}{9}(1+y^2)}\quad\quad(t\equiv \frac{\sqrt{5}}{3}y)\\&=&\frac{2}{\sqrt{5}}\int^\infty_{-\infty}\frac{dy}{1+y^2}\\&=&\frac{2}{\sqrt{5}}\Bigl[\arctan y\Bigr]^\infty_{-\infty}\\&=&\frac{2}{\sqrt{5}}\pi\end{eqnarray}最後ところで「$\arctan$ なんて知らんよ!」という場合は $y=\tan\theta$ と置換して計算してください。
$$ \int_0^{2\pi}\frac{dx}{3+2\sin x} = \frac{2}{\sqrt{5}}\pi $$
これで積分ができました。冒頭で「泥臭い」といったのがなんとなく分かるのではないでしょうか。でも求まるととても気持ちいいですね。
今回求めた積分は「複素積分」を用いて解くことも可能です。また記事にしたいと思います。しました。
せっかくなので例題を掲載します。
定積分$$\int_0^\frac{\pi}{2} \frac{1+\cos x}{(1+\sin x)^2}dx$$をワイエルシュトラス置換により解け.
ワイエルシュトラス置換 $\tan\displaystyle\frac{x}{2}=t$ により$$\cos x=\frac{1-t^2}{1+t^2} \;,\; \sin x =\frac{2t}{1+t^2}$$$$dx=\frac{2dt}{1+t^2}$$$t$ の範囲は $[0,1]$ となりますので$$ \int_0^\frac{\pi}{2} \frac{1+\cos x}{(1+\sin x)^2}dx =\int_0^1 \frac{1+ \frac{1-t^2}{1+t^2} }{(1+ \frac{2t}{1+t^2})^2} \frac{2dt}{1+t^2} $$計算すると$$=4\int^1_0\frac{dt}{(t+1)^4}=-\frac{4}{3}\left[\frac{1}{(t+1)^3}\right]_0^1$$$$\therefore\quad \int_0^\frac{\pi}{2} \frac{1+\cos x}{(1+\sin x)^2}dx =\frac{7}{6}$$
定積分$$\int^\pi_0\frac{dx}{2-\sin^2x}$$をワイエルシュトラス置換により解け.
ワイエルシュトラス置換 $\tan\displaystyle\frac{x}{2}=t$ により\begin{eqnarray*}\int^\pi_0\frac{dx}{2-\sin^2x}&=&\int_0^\infty \frac{1}{2- (\frac{2t}{1+t^2})^2 } \frac{2dt}{1+t^2} \\ &=&\int_0^\infty\frac{1+t^2}{(1+t^2)^2-2t^2}dt\\ &=&\int_0^\infty\frac{1+t^2}{(t^2+\sqrt{2}t+1)(t^2-\sqrt{2}t+1)}dt\end{eqnarray*}
ここで部分分数分解を$$ \frac{1+t^2}{(t^2+\sqrt{2}t+1)(t^2-\sqrt{2}t+1)} =\frac{at+b}{ t^2+\sqrt{2}t+1 }+ \frac{ct+d}{ t^2-\sqrt{2}t+1 }$$とおけば恒等式の係数比較$$\begin{cases}1&=&b+d\\0&=&a+c+\sqrt{2}(d-b) \\ 1 &=&\sqrt{2}(c-a)+b+d\\ 0&=& a+c\end{cases}$$によって $a=c=0$ , $b=d=1/2$ となります。従って積分は\begin{eqnarray*}\int^\pi_0\frac{dx}{2-\sin^2x} &=&\int_0^\infty\left( \frac{\frac{1}{2}}{t^2+\sqrt{2}t+1}+\frac{\frac{1}{2}}{t^2-\sqrt{2}t+1}\right)dt\\ &=&\frac{1}{2}\int_0^\infty\left[\frac{1}{\left(t+\frac{1}{\sqrt{2}}\right)^2+\frac{1}{2}}+\frac{1}{\left(t-\frac{1}{\sqrt{2}}\right)^2+\frac{1}{2}}\right]dt\end{eqnarray*}
第1項を $t+\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}\tan\theta$ , 第2項を $t-\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}\tan\theta$ と置換すると、ともに$$dt=\frac{d\theta}{\sqrt{2}\cos^2\theta}$$と置きかわります。下表が積分範囲になります。
| $t$ | $0$ | $\rightarrow$ | $\infty$ |
| $\theta$ | $\frac{\pi}{4}$ | $\rightarrow$ | $\frac{\pi}{2}$ |
| $t$ | $0$ | $\rightarrow$ | $\infty$ |
| $\theta$ | -$\frac{\pi}{4}$ | $\rightarrow$ | $\frac{\pi}{2}$ |
以上から求める積分は\begin{eqnarray*} \int^\pi_0\frac{dx}{2-\sin^2x} &=&\frac{1}{2}\int^\frac{\pi}{2}_{\frac{\pi}{4}}\frac{1}{\frac{1}{2}\tan^2\theta+\frac{1}{2}}\frac{d\theta}{\sqrt{2}\cos^2\theta}+\frac{1}{2}\int^\frac{\pi}{2}_{-\frac{\pi}{4}}\frac{1}{\frac{1}{2}\tan^2\theta+\frac{1}{2}}\frac{d\theta}{\sqrt{2}\cos^2\theta}\\ &=&\frac{1}{\sqrt{2}} \int^\frac{\pi}{2}_{\frac{\pi}{4}} d\theta+ \frac{1}{\sqrt{2}} \int^\frac{\pi}{2}_{-\frac{\pi}{4}} d\theta \\&=&\frac{\pi}{\sqrt{2}}\end{eqnarray*}
$$I:=\int_0^1\frac{dx}{(1+sx)\sqrt{1-x^2}}\quad(-1\le s\le 1)$$
根号を消したいので $x=\sin\t$ とすると$$I=\int_0^\frac{\pi}{2}\frac{d\t}{1+s\sin\t}$$ワイエルシュトラス置換 $\tan\displaystyle\frac{\t}{2}=t$ により$$I=2\int_0^1\frac{dt}{t^2+2st+1}$$分母を平方完成します。$$I=2\int_0^1\frac{dt}{(t+s)^2+1-s^2}$$$t+s=\sqrt{1-s^2}\tan\t$ とおくと$$I=\frac{2(\beta-\a)}{\sqrt{1-s^2}}$$ただし $\a$ , $\b$ は$$\tan\a=\frac{s}{\sqrt{1-s^2}}\quad,\quad\tan\b=\frac{1+s}{\sqrt{1-s^2}}$$を満たします。ここで $\tan$ の加法定理より$$\tan(\b-\a)=\sqrt{\frac{1-s}{1+s}}$$さらに倍角をとって$$\tan2(\b-\a)=\frac{\sqrt{1-s^2}}{s}$$簡単な三角比の関係から$$\cos2(\b-\a)=s$$と書けますので$$2(\b-\a)=\arccos s$$$$\therefore\quad\int_0^1\frac{dx}{(1+sx)\sqrt{1-x^2}}=\frac{\arccos s}{\sqrt{1-s^2}}$$
$$I=\int_0^1\frac{dx}{(1+x^2)\sqrt{2+x^2}}$$において, $x=\sqrt{2}\tan\t$ と置換した後、ワイエルシュトラス置換によって積分を計算せよ。
$I$ の計算は実はもっと効率的な方法があるのですが、ワイエルシュトラス置換の練習として遠回りします。まず$$I=\int_0^\a \frac{d\t}{(1+2\tan^2\t)\cos\t}\quad,\quad \a:=\arctan\frac{1}{\sqrt{2}}$$ここでワイエルシュトラス置換をすると\begin{align}&=2\int_0^{\sqrt{3}-\sqrt{2}}\frac{1-t^2}{t^4+6t^2+1}dt\\&=\int_0^{\sqrt{3}-\sqrt{2}}\left(-\frac{\sqrt{2}+1}{t^2+2\sqrt{2}+3}+\frac{\sqrt{2}-1}{t^2-2\sqrt{2}+3}\right)\\&=\left[-\arctan\left(\frac{t}{\sqrt{2}+1}\right)+\arctan\left(\frac{t}{\sqrt{2}-1}\right)\right]_0^{\sqrt{3}-\sqrt{2}}\\&=\underbrace{\arctan\left(\frac{\sqrt{3}-\sqrt{2}}{\sqrt{2}-1}\right)}_{\t_1}-\underbrace{\arctan\left(\frac{\sqrt{3}-\sqrt{2}}{\sqrt{2}+1}\right)}_{\t_2}\end{align}加法定理により$$\tan(\t_1-\t_2)=\frac{1}{\sqrt{3}}$$となるので$$\t_1-\t_2=\arctan\frac{1}{\sqrt{3}}=\frac{\pi}{6}$$
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。