微分幾何学の講座・第6回。曲面の第1基本量、第2基本量およびそれらを用いた基本形式を紹介します。第1基本量は接ベクトルを使って曲面の性質を表します。第2基本量は法ベクトルも用います。第1基本量、第1基本形式を用いて曲面を論じることを「内在幾何」といいますが、このあたりの話はしばらく先の記事になりそうです。
前回はこちら:
空間内の曲面:パラメータ表示、接平面、法ベクトル、ガウス写像、面積
領域 $D$ で定義されるパラメータ $u,v$ を用いて、空間内の曲面は\begin{equation}\bm{S}(u,v):=\bigl(x(u,v),y(u,v),z(u,v)\bigr)\;\quad u,v\in D\tag{1}\end{equation}と表現される。
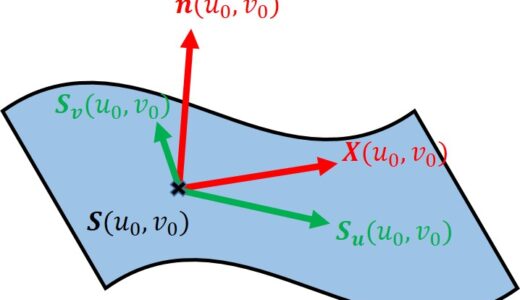
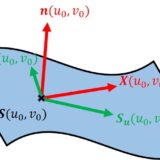
曲面上の点 $\bm{S}(u,v)$ において$$\dd{\bm{S}}{u}(u,v)\quad,\quad\dd{\bm{S}}{v}(u,v)$$の2つは曲面の接ベクトルであり、曲面を論じるときは、これらが1次独立であることを前提とする。
曲面上の点 $\bm{S}(u,v)$ における単位法ベクトルを次で定義する。\begin{equation}\bm{n}(u,v):=\frac{\bm{S}_u(u,v)\times\bm{S}_v(u,v)}{|\bm{S}_u(u,v)\times\bm{S}_v(u,v)|}\tag{2}\end{equation}
$v$ を固定すると $\bm{S}(u,v)$ の実質のパラメータは1つであるため、曲面内の曲線を描く、これを $u$ 曲線という。同様に $u$ を固定して描かれる曲線を $v$ 曲線という。
詳細は前回の記事を参照してください。
\begin{equation}\mathrm{I}:=Edu^2+2Fdudv+Gdv^2\tag{3}\end{equation}を曲面 $\bm{S}(u,v)$ の「第1基本形式」という。ここで\begin{eqnarray}E&:=&\bm{S}_u\cdot \bm{S}_u\tag{4a}\\ F&:=&\bm{S}_u\cdot \bm{S}_v\tag{4b}\\ G&:=&\bm{S}_v\cdot \bm{S}_v\tag{4c}\end{eqnarray}を曲面 $\bm{S}(u,v)$ の「第1基本量」とよぶ。
また\begin{equation}\mathrm{I}=d\bm{S}\cdot d\bm{S}\tag{5}\end{equation}である。
加えて、第1基本量に関する行列 $\mathcal{G}$ を\begin{equation}\mathcal{G} := \begin{pmatrix}E & F\\F & G\end{pmatrix}\tag{6}\end{equation}で定義し、第1基本行列とよぶ。
2つの接ベクトルの組み合わせを選んで内積をとったものが、それぞれ $E,F,G$ です。(5)については$$d\bm{S}=\bm{S}_udu+\bm{S}_vdv$$を使って $d\bm{S}\cdot d\bm{S}$ を計算すると簡単に示せます。
このとき(4)より\begin{equation}\det\mathcal{G}=EG-F^2=|\bm{S}_u\times\bm{S}_v|^2\tag{7}\end{equation}また定義より明らかに $E>0$ ですので $\mathcal{G}$ の首座小行列式はすべて正。よって $\mathcal{G}$ は正定値ですので、任意の行ベクトル $z$ に対して\begin{equation}z\mathcal{G}z^T>0\tag{8}\end{equation}です。
さらに行ベクトル $\sigma :=(du,dv)$ に対し\begin{equation}\mathrm{I}=\sigma\:\mathcal{G}\:\sigma^T\tag{9}\end{equation}であることを簡単に確認できます。
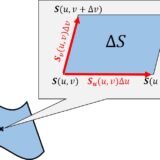
前回記事より、曲面の面積は\begin{equation}S=\iint_D |\bm{S}_u\times\bm{S}_v|dudv\tag{10}\end{equation}でした。(7)より\begin{equation}S=\iint_D\sqrt{\det\mathcal{G}}\:dudv\tag{11}\end{equation}であることが示されます。
\begin{equation}\mathrm{II}:=Ldu^2+2Mdudv+Ndv^2\tag{12}\end{equation}を曲面 $\bm{S}(u,v)$ の「第2基本形式」という。ここで\begin{eqnarray}L&:=&\bm{S}_{uu}\cdot \bm{n}\tag{13a}\\ M&:=&\bm{S}_{uv}\cdot \bm{n}\tag{13b}\\ N&:=&\bm{S}_{vv}\cdot \bm{n}\tag{13c}\end{eqnarray}を曲面 $\bm{S}(u,v)$ の「第2基本量」とよぶ。
また\begin{equation}\mathrm{II}=-d\bm{S}\cdot d\bm{n}\tag{14}\end{equation}である。
加えて、第2基本量に関する行列 $\mathcal{H}$ を\begin{equation}\mathcal{H} := \begin{pmatrix}L & M\\M & N\end{pmatrix}\tag{15}\end{equation}で定義し、第2基本行列とよぶ。
2階微分と単位法ベクトル $\bm{n}$ の内積をとっています。
(13)には別の表現もあります。接ベクトルと法ベクトルは直交しますので$$\bm{S}_u\cdot\bm{n}=\bm{S}_v\cdot\bm{n}=0$$これを微分することにより\begin{eqnarray}\bm{S}_{uu}\cdot \bm{n}&=&-\bm{S}_{u}\cdot \bm{n}_{u} \\\bm{S}_{uv}\cdot \bm{n}&=&-\bm{S}_{u}\cdot \bm{n}_{v}=-\bm{S}_{v}\cdot \bm{n}_{u}\tag{16}\\\bm{S}_{vv}\cdot \bm{n}&=&-\bm{S}_{v}\cdot \bm{n}_{v}\end{eqnarray}が成立するので\begin{eqnarray}L&=&-\bm{S}_{u}\cdot \bm{n}_{u}\\ M&=&-\bm{S}_{u}\cdot \bm{n}_{v}\tag{17}\\ N&=&-\bm{S}_{v}\cdot \bm{n}_{v}\end{eqnarray}とも書けます。
(14)は(5)と同じ要領で示せます。また(9)と同様に\begin{equation}\mathrm{II}=\sigma\:\mathcal{H}\:\sigma^T\tag{18}\end{equation}
第1基本形式では接ベクトルのみを扱ったのでイメージがしやすかったのに対し、第2基本形式は2階微分なので分かりづらいです。$v$ を固定して考えてみましょう。このとき $u$ を動かせば $\bm{S}$ は曲面内の $u$ 曲線を描きます。よって $\bm{S}_u$ はこの曲線の接ベクトルです。$\bm{S}_{uu}$ は接ベクトルの変化を表します。$u$ が弧長パラメータなら$\bm{S}_{uu}$ は曲率中心を向きますが、一般のパラメータではそうとは限りません。その代わり、(13a)より $L$ は$\bm{S}_{uu}$ と法ベクトルの内積ですので、$L$ は $\bm{S}_{uu}$ を $\bm{S}_u$ 方向と $\bm{n}$ 方向に分解したときの $\bm{n}$ 成分となります(当然 $\bm{S}_u\perp\bm{n}$)。
$\bm{S}(u,v)$ の $v$ を固定しているとき、接ベクトルが一定なら $\bm{S}_{uu}=0$ なので $L=0$ です。接ベクトルが一定ではないが向きを変えないとすると $\bm{S}_{uu}\parallel \bm{S}_u$ なので $\bm{S}_{uu}\perp\bm{n}$ となって、やはり $L=0$ です。このことから $u$ 曲線が直線なら $L=0$ となります。
いろいろ考察する余地がありますが、私も含め初学者にはすぐにはイメージが付きづらいもの。のちに紹介する例題を通して考えるのもいいと思います。
追記:小林昭七『曲線と曲面の微分幾何』によると、$\det\mathcal{H}>0$ となる点では曲面は凸(または凹)であり、$\det\mathcal{H}<0$ となる点では鞍状となります。同書に証明もあり。
初歩的な例を見ていきましょう。
半径 $a$ の球面$$\bm{S}(u,v):=\bigl(a\cos u\cos v,a\cos u\sin v, a\sin u\bigr)\;,\;-\frac{\pi}{2}\le u \le\frac{\pi}{2}\:,\:0\le v<2\pi$$の第1基本形式および第2基本形式を求めよ。
$$\bm{S}_u=\begin{pmatrix}-a\sin u\cos v\\-a\sin u\sin v\\a\cos u\end{pmatrix}\;,\;\bm{S}_v=\begin{pmatrix}-a\cos u\sin v\\a\cos u\cos v\\0\end{pmatrix}$$より$$E=a^2\;,\;F=0\;,\;G=a^2\cos^2u$$となる。また単位法ベクトルは $\bm{S}_u\times\bm{S}_v$ 方向の単位ベクトルなので$$\bm{n}(u,v)=\begin{pmatrix}-\cos u\cos v\\-\cos u\sin v\\\sin u\end{pmatrix}=-\frac{1}{a}\bm{S}$$さらに微分すると$$\bm{S}_{uu}=\begin{pmatrix}-a\cos u\cos v\\-a\cos u\sin v\\-a\sin u\end{pmatrix}=-\bm{S}\;,\;\bm{S}_{vv}=\begin{pmatrix}-a\cos u\cos v\\-a\cos u\sin v\\0\end{pmatrix}$$$$\bm{S}_{uv}=\begin{pmatrix}a\sin u\sin v\\-a\sin u\cos v\\0\end{pmatrix}$$したがって$$L=a\;,\;M=0\;,\;N=a\cos^2u$$以上より第1基本形式および第2基本形式は\begin{eqnarray*}\mathrm{I}&=&a^2du^2+a^2\cos^2udv^2\\\mathrm{II}&=& adu^2+a\cos^2udv^2\end{eqnarray*}
楕円放物面$$\bm{S}(u,v):=\bigl(au,bv, u^2+v^2\bigr)\;,\quad u,v\in\RR$$の第1基本形式および第2基本形式を求めよ。
$$E=a^2+4u^2\;,\;F=4uv\;,\; G=b^2+4v^2$$$$L=N=\frac{2ab}{\sqrt{4b^2u^2+4a^2v^2+a^2b^2}}\;,\;M=0$$より求まります。
曲面 $z=f(x,y)$ の第1基本形式および第2基本形式を求めよ。
$\bm{S}(u,v)=\bigl(u,v,f(u,v)\bigr)$ とできるので$$E=1+f_u^2\;,\;F=f_uf_v,G=1+f_v^2$$$$L=\frac{f_{uu}}{\sqrt{1+f_u^2+f_v^2}}\;,\;M=\frac{f_{uv}}{\sqrt{1+f_u^2+f_v^2}}\;,\;N=\frac{f_{vv}}{\sqrt{1+f_u^2+f_v^2}}$$より求まります。
無限に長い円柱$$\bm{S}(u,v):=\bigl(a\cos u,a\sin u, v\bigr)\;,\quad 0\le u< 2\pi\;,\;v\in\RR$$の $u$ 曲線と $v$ 曲線はどのようなものか。また第1基本形式および第2基本形式を求めよ。
$\bm{S}_u=(-a\sin u,a\cos u,0)$ , $\bm{S}_v=(0,0,1)$ より $u$ 曲線は $xy$ 平面に平行な円、$v$ 曲線は $z$ 軸に平行な直線。また $\bm{n}=(\cos u,\sin u,0)$ であり $\bm{S}_{uu}=(-a\cos u,-a\sin u,0)$ , $\bm{S}_{uv}=\bm{S}_{vv}=0$ である。よって$$I=a^2du^2+dv^2$$$$II=-adu^2$$ちなみに第2基本形式は$$d\bm{S}\cdot d\bm{n}=-a du^2$$とも書けるのでした。右辺を見ると $dv$ がありませんが、これは $v$ が変化しても $\mathrm{II}$ は不変ということです。実際に図を想像すると $v$ を変化させても $\bm{S}$ の変化は $z$ 方向のみで $\bm{n}$ は不変、よって $d\bm{S}$ と $d\bm{n}$ の内積はゼロとなります。
$xyz$ 空間内にある曲面があるとき、それを $u,v$ によってパラメータ表示する方法はいくらでもあるのでした。いま、その曲面を $\bm{S}(u,v)$ で表せたとします。パラメータの変換$$u'=u'(u,v)\;,\; v'=v'(u,v)$$を考えます。その逆は$$u=u(u',v')\;,\; v=v(u',v')$$です。すると $\bm{S}(u,v)=\bm{S}\bigl(u(u',v'),v(u',v')\bigr):=\bm{S}'(u',v')$ なる新しいパラメータ表示が定義されます。
このあたらしいパラメータ表示において第1基本量を計算してみましょう。$\bm{S}'(u',v')$ の1階偏微分が必要です。$$\dd{\bm{S}'}{u'}=\dd{S(u,v)}{u'}=\dd{\bm{S}}{u}\dd{u}{u'}+\dd{\bm{S}}{v}\dd{v}{u'}$$$$\therefore\quad\dd{\bm{S}'}{u'}=\bm{S}_u\dd{u}{u'}+\bm{S}_v\dd{v}{u'}$$同様に $v'$ による偏微分も計算し、まとめて表現すると\begin{equation}\begin{pmatrix}\bm{S}'_{u'}\\\bm{S}'_{v'}\end{pmatrix}=\begin{pmatrix}\dd{u}{u'} & \dd{v}{u'}\\ \dd{u}{v'} & \dd{v}{v'}\end{pmatrix}\begin{pmatrix}\bm{S}_{u}\\\bm{S}_{v}\end{pmatrix}\tag{19}\end{equation}右辺に現れた正方行列をヤコビ行列といい、$J$ と書きます。(19)により外積は$$\bm{S}'_{u'}\times\bm{S}'_{v'}=\det J\;(\bm{S}_{u}\times\bm{S}_{v})$$長さ1に規格化したものが単位法ベクトルなので、計算すると\begin{equation}\bm{n}'=\mathrm{sgn}(\det J)\bm{n}\tag{20}\end{equation}つまりパラメータを変換しても単位法ベクトルは不変(またはその負号つき)であることが分かります。分かりやすくパラメータを明示すると$$\bm{n}'(u',v')=\bm{n}(u,v)\;\mathrm{or}\;-\bm{n}(u,v)$$です。
よって第1基本形式は\begin{eqnarray*}\mathrm{I}'&=&(d\bm{S}')^2 \\&=& \left(\bm{S}'_{u'}du'+\bm{S}'_{v'}dv'\right)^2 \\&=& \left[\left(\dd{u}{u'}\bm{S}_u+\dd{v}{u'}\bm{S}_v\right)\left(\dd{u'}{u}du+\dd{u'}{v}dv\right)+\left(\dd{u}{v'}\bm{S}_u+\dd{v}{v'}\bm{S}_v\right)\left(\dd{v'}{u}du+\dd{v'}{v}dv\right)\right]^2\\&=&\biggl[\left\{\bm{S}_u\left(\dd{u}{u'}\dd{u'}{u}+\dd{u}{v'}\dd{v'}{u}\right)+\bm{S}_v\left(\dd{v}{u'}\dd{u'}{u}+\dd{v}{v'}\dd{v'}{u}\right)\right\}du\\&&+\left\{\bm{S}_u\left(\dd{u}{u'}\dd{u'}{v}+\dd{u}{v'}\dd{v'}{v}\right)+\bm{S}_v\left(\dd{v}{u'}\dd{u'}{v}+\dd{v}{v'}\dd{v'}{v}\right)\right\}dv\biggr]^2\\ &=&[\bm{S}_udu+\bm{S}_vdv]^2 \\&=& \mathrm{I}\end{eqnarray*}すなわち第1基本形式は不変です。なお第1基本量それぞれは不変ではありません。計算すれば\begin{eqnarray*}E' &=&E\left(\dd{u}{u'}\right)^2+2F\dd{u}{u'}\dd{v}{u'}+G\left(\dd{v}{u'}\right)^2 \\ F' &=& E\dd{u}{u'}\dd{u}{v'}+F\left(\dd{u}{u'}\dd{v}{v'}+\dd{v}{u'}\dd{u}{v'}\right)+G\dd{v}{u'}\dd{v}{v'}\\ G' &=& E\left(\dd{u}{v'}\right)^2+2F\dd{u}{v'}\dd{v}{v'}+G\left(\dd{v}{v'}\right)^2\end{eqnarray*}となります。
ちなみに第2基本形式は $\mathrm{II}'=\mathrm{II}$ または負号のついたものになります。
第3基本形式というのもあって、\begin{equation}\mathrm{III}:=d\bm{n}\cdot d\bm{n}\tag{21}\end{equation}と定義します。ここで$$d\bm{n}=\bm{n}_udu+\bm{n}_v dv$$です。計算により、次を示すことができます。\begin{equation}K\mathrm{I}-2H\mathrm{II}+\mathrm{III}=0\tag{22}\end{equation}
・中内伸光『幾何学は微分しないと』(下記)
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。初学者向けな分、内容はやや薄いと思うので、ネットや他の書籍を併用すると学習効果が高まります。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
次は:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。