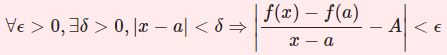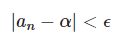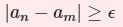前回は $\epsilon-N$ 論法を用いた数列の収束について説明しました。
今回はそれを応用してコーシー列について説明します。コーシー列とは$$\displaystyle\lim_{n,m\to\infty}|a_n-a_m|=0$$を満たす数列 $\{a_n\}$ を指します。$n,m$ が大きくなるにつれて数列の変化がどんどんなくなっていくよってことです。これを $\epsilon-N$ 論法で表現すると下のようになります。
任意の $\epsilon>0$ に対してある自然数 $N$ が存在し$$m,n\ge N \Rightarrow |a_n-a_m|<\epsilon$$とできる。
$a_n$ と $a_m$ の差が限りなく $0$ に近づくということを表現したいわけです。目標は「$\epsilon$ がどんなに小さくても、$m,n$ が大きければ $|a_n-a_m|<\epsilon$ と書ける」ということです。そのように書ける $m,n$ ってどれくらい大きいの?というと、$N$ 以上の大きさですよということをいっています。その $N$ は $\epsilon$ に依存しますから、どんな $\epsilon$ に対しても存在することを示す(ときには $N$ を $\epsilon$ の式であらわす)といいわけです。
実数の世界では「数列が収束すること」と「数列がコーシー列であること」は同値ですので(後述)、コーシー列であることを示せば数列が収束することを示せたことになります。普通に数列の収束を示す $|a_n-\alpha|<\epsilon$ の場合と比べて、コーシー列であることを示す場合は収束先の極限値が分からなくてもいいのがメリットです。
$a_n=\displaystyle\frac{1}{2^n}$ はコーシー列である。
うまく $N$ を見つけてみましょう。三角不等式が使えそうです。$$|a_n-a_m|=\left| \frac{1}{2^n}-\frac{1}{2^m}\right|\le\frac{1}{2^n}+\frac{1}{2^m}\le\frac{1}{2^N}+\frac{1}{2^N}=\frac{1}{2^{N-1}}$$よって任意の $\epsilon$ に対して $\displaystyle\frac{1}{2^{N-1}}<\epsilon$ を満たすように $N$ をとれば、$m,n\ge N$ ならば$$|a_n-a_m|\le\frac{1}{2^{N-1}}<\epsilon$$と書けることが分かり、コーシー列であるといえます。$N$ の値を具体的にもってこいよといわれたら、例えば$$N=1+\lceil \log_2\frac{1}{\epsilon}\rceil$$とすればいいです。
$a_n=1+\displaystyle\frac{1}{2^2}+\cdots\frac{1}{n^2}$ はコーシー列である。
$N$ を探しますが、この際 $m\ge n\ge N$として一般性を失いません。\begin{eqnarray*}|a_n-a_m|&=&\frac{1}{(n+1)^2}+\frac{1}{(n+2)^2}+\cdots+\frac{1}{m^2}\\ &<&\frac{1}{n(n+1)}+\frac{1}{(n+1)(n+2)}+\cdots+\frac{1}{(m-1)m}\\ &=& \left(\frac{1}{n}-\frac{1}{n+1}\right) + \left(\frac{1}{n+1}-\frac{1}{n+2}\right)+\cdots+ \left(\frac{1}{m-1}-\frac{1}{m}\right)\\ &=& \frac{1}{n}-\frac{1}{m}\\ &<& \frac{1}{n}\\&\le&\frac{1}{N} \end{eqnarray*}よって $1/N<\epsilon$ となるように$N$をとればOKです。
この数列の極限はゼータ関数(の引数2)としてよく知られており、$\pi^2/6$に収束します。なのでもし普通に数列の収束性を示すなら$$\forall n>N \;,\;\left|a_n- \frac{\pi^2}{6}\right|<\epsilon$$なる $N$ を探さなければならず、何だか難しそうですよね。なので極限値が分からなくてもいいから収束するか知りたいときはコーシー列が便利です。
実数の世界では、数列が収束することとコーシー列であることは同値です。これを示してみようと思います。
収束する数列 $\{a_n\}$ はコーシー列である.
【証明】数列 $\{a_n\}$ が収束するので任意の $\epsilon>0$ に対し自然数 $N$ が存在し$$n\ge N\Longrightarrow |a_n-\alpha|<\epsilon$$とできます。$\epsilon$ はまったく任意なので $\epsilon/2$ としても同様に書けるはずですから(もちろんとるべき $N$ の値は変わります)$$m,n\ge N\Longrightarrow\begin{cases}|a_m-\alpha|&<&\displaystyle\frac{\epsilon}{2}\\ |a_n-\alpha|&<&\displaystyle\frac{\epsilon}{2}\end{cases}$$これを用いて\begin{eqnarray*}|a_m-a_n|&=&|(a_m-\alpha)-(a_n-\alpha)|\\&\le& |a_m-\alpha|+|a_n-\alpha|\\&<&\frac{\epsilon}{2}+ \frac{\epsilon}{2}=\epsilon\end{eqnarray*}これは冒頭のコーシー列の定義そのものです。
コーシー列 $\{a_n\}$ は収束する.
【証明】コーシー列より任意の $\epsilon>0$ に対してある自然数 $N_1$ が存在して\begin{eqnarray}m,n> N_1&\Longrightarrow&|a_n-a_m|<\frac{\epsilon}{2}\\&\Longleftrightarrow& a_m-\frac{\epsilon}{2}<a_n<a_m+\frac{\epsilon}{2}\tag{1}\end{eqnarray}この $m>N_1$ について\begin{eqnarray*}x&=&\min\left\{a_1,a_2,\cdots,a_{N_1},a_m-\frac{\epsilon}{2}\right\}\\ y&=&\max\left\{a_1,a_2,\cdots,a_{N_1},a_m+\frac{\epsilon}{2}\right\}\end{eqnarray*}と定義します。$n$ が $1,2,\cdots, N_1$ のどれかなら $a_n$ は $a_1$~$a_{N_1}$ のどれかなので $x\le a_n\le y$ となります。$n>N_1$ なら(1)の不等式が成立するので $a_n>a_m-\frac{\epsilon}{2}\ge x$ および $a_n<a_m+\frac{\epsilon}{2}\le y$ となります。よって$$\forall n\in\mathbb{N}\;,\; x\le a_n\le y$$これは $\{a_n\}$ が有界であることを示しています。
ボルツァーノ=ワイエルシュトラスの定理によれば「有界な数列は、収束する部分列をもつ」ので $\{a_n\}$ には極限 $\alpha$ に収束する部分列があります。これを添え字の小さい方から順に並べて$$\{a_{n_k}\}\equiv\{a_{n_1},a_{n_2},\cdots,a_{n_k},\cdots\}$$とします。すると先ほどの $\epsilon$ に対してある自然数 $N_2$ が存在し$$n_k>N_2\Longrightarrow |a_{n_k}-\alpha|<\frac{\epsilon}{2}$$とできることになります。$N=\max\{N_1,N_2\}$ ととれば\begin{eqnarray*}n,n_k>N\Longrightarrow |a_n-\alpha|&\le&|a_n-a_{n_k}|+|a_{n_k}-\alpha|\\&<&\frac{\epsilon}{2}+ \frac{\epsilon}{2} =\epsilon\end{eqnarray*}よって数列 $\{a_n\}$ は収束します。
以上、収束することとコーシー列であることが同値であることが示されました。
収束しないことを示すには「コーシー列でない」ことを示せばいいですね。これについては次回とりあげます。
ε論法シリーズ
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。