重積分\begin{equation}I\equiv\int_0^1\int_0^1\frac{dxdy}{1-xy}\tag{1}\end{equation}を用いて$$\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}$$を示せ。
参考にした論文は
(1)を級数展開して積分を実行するとゼータ関数が現れます。\begin{eqnarray*}I&&=\int_0^1\int_0^1\frac{dxdy}{1-xy}\\&&=\int_0^1\left(\int_0^1(1+xy+x^2y^2+x^3y^3+\cdots)dx\right)dy\\&&=\int_0^1\left[x+\frac{x^2}{2}y+\frac{x^3}{3}y^2+\frac{x^4}{4}y^3+\cdots\right]_{x=0}^1dy\\&&=\int_0^1\left(1+\frac{1}{2}y+\frac{1}{3}y^2+\frac{1}{4}y^3+\cdots\right)dy\\&&=\left[y+\frac{y^2}{2^2}+\frac{y^3}{3^2}+\frac{y^4}{4^2}\cdots\right]_0^1\\&&=\sum_{n=1}^\infty\frac{1}{n^2}\end{eqnarray*}よって次のことが言えます。
\begin{equation}\int_0^1\int_0^1\frac{dxdy}{1-xy}=\zeta(2)\tag{2}\end{equation}
一方、$I$ において\begin{equation}x=\frac{u-v}{\sqrt{2}}\quad,\quad y=\frac{u+v}{\sqrt{2}}\tag{3}\end{equation}と、座標軸の回転に相当する置換をするとヤコビアンは$$|J|=\left|\begin{matrix}\frac{1}{\sqrt{2}}&&-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&&\frac{1}{\sqrt{2}}\end{matrix}\right|=1$$です。正方形である積分範囲 $D$ は下図を参考にして$$\begin{cases}-u\le v\le u&\quad&(0\le u\le \frac{1}{\sqrt{2}})\\u-\sqrt{2}\le v\le -u+\sqrt{2}&\quad&(\frac{1}{\sqrt{2}}\le u\le\sqrt{2})\end{cases}$$
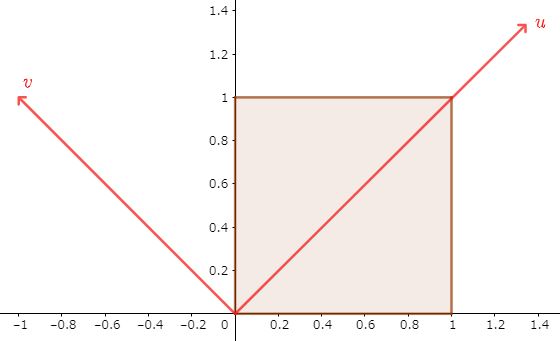
$I$ は $x,y$ について対称ですから正方形を $x=y$ で等分した左側のほうのみ考えればよいです。\begin{eqnarray*}I&&=\iint_D\frac{dxdy}{1-xy}\\&&=\iint_D\frac{dudv}{1-\frac{u^2-v^2}{2}}\\&&=2\iint_D\frac{dudv}{2-u^2+v^2}\\&&=2\int_0^{\frac{1}{\sqrt{2}}}\left(\int_{-u}^u\frac{dv}{2-u^2+v^2}\right)du\\&&\quad\quad+2\int_{\frac{1}{\sqrt{2}}}^\sqrt{2}\left(\int_{u-\sqrt{2}}^{-u+\sqrt{2}}\frac{dv}{2-u^2+v^2}\right)du\\&&=4\int_0^{\frac{1}{\sqrt{2}}}\left(\int_0^u\frac{dv}{2-u^2+v^2}\right)du\\&&\quad\quad+4\int_{\frac{1}{\sqrt{2}}}^\sqrt{2}\left(\int_0^{-u+\sqrt{2}}\frac{dv}{2-u^2+v^2}\right)du\end{eqnarray*}ここで$$\int\frac{dx}{x^2+a^2}=\frac{1}{a}\arctan\frac{x}{a}$$を用いると\begin{eqnarray*}I&&=4\int_0^{\frac{1}{\sqrt{2}}}\frac{1}{\sqrt{2-u^2}}\left[\arctan\frac{v}{\sqrt{2-u^2}}\right]_0^u du\\&&\quad\quad+4\int_{\frac{1}{\sqrt{2}}}^\sqrt{2}\frac{1}{\sqrt{2-u^2}}\left[\arctan\frac{v}{\sqrt{2-u^2}}\right]_0^{\sqrt{2}-u}du\\&&=4\int_0^{\frac{1}{\sqrt{2}}}\frac{1}{\sqrt{2-u^2}}\arctan\frac{u}{\sqrt{2-u^2}} du\\&&\quad\quad+4\int_{\frac{1}{\sqrt{2}}}^\sqrt{2}\frac{1}{\sqrt{2-u^2}}\arctan\frac{\sqrt{2}-u}{\sqrt{2-u^2}}du\end{eqnarray*}
$u=\sqrt{2}\sin\t$ と置換すると\begin{eqnarray*}I&&=4\int_0^\frac{\pi}{6}\arctan(\tan\t)d\t+4\int_\frac{\pi}{6}^\frac{\pi}{2}\arctan\frac{1-\sin\t}{\cos\t}d\t\\&&=4\int_0^\frac{\pi}{6}\t d\t+4\int_\frac{\pi}{6}^\frac{\pi}{2}\arctan\frac{1-\frac{2\tan(\t/2)}{1+\tan^2(\t/2)}}{\frac{1-\tan^2(\t/2)}{1+\tan^2(\t/2)}}d\t\\&&=\frac{\pi^2}{18}+4\int_\frac{\pi}{6}^\frac{\pi}{2}\arctan\frac{1-\tan\frac{\t}{2}}{1+\tan\frac{\t}{2}}d\t\\&&=\frac{\pi^2}{18}+4\int_\frac{\pi}{6}^\frac{\pi}{2}\arctan\left(\tan\left(\frac{\pi}{4}-\frac{\t}{2}\right)\right)d\t\\&&=\frac{\pi^2}{18}+4\int_\frac{\pi}{6}^\frac{\pi}{2}\left(\frac{\pi}{4}-\frac{\t}{2}\right)d\t\\&&=\frac{\pi^2}{6}\end{eqnarray*}よって次の式が成立します。
\begin{equation}\int_0^1\int_0^1\frac{dxdy}{1-xy}=\frac{\pi^2}{6}\tag{4}\end{equation}
(2)(4)によって求めていた式を得ます。
$$\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}$$
これと似た重積分を使う方法はこちら:
過去にもゼータの値については扱っています:
ゼータ関数の基礎シリーズ第1回はこちらから!
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。





≪…バーゼル問題…≫を、[句]
〇÷□如来蔵
令和6年4月に開設の岡潔数学体験館で、自然数のキュレーション的な催しがあるといいなぁ~