「ゼータ関数の基礎」シリーズ第2回です。前回はフルヴィッツゼータ関数の積分表示を導出しました。シリーズ外の過去記事の紹介もしているので、まずはご覧ください:
もくじ
ゼータ関数の複素積分表示と留数
$\mathfrak{R}s>1$ かつ $s\notin\NN$ で前回の記事を応用すると\begin{equation}\zeta(s,a)=-\frac{\G(1-s)}{2\pi i}\int_C\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz\tag{1}\end{equation}ただし $C$ はハンケル積分路(下図)。

しかもこの表示において $\zeta(s,a)$ は $s=1,2,3\cdots$ を除く全平面で成立する。また $s=1$ で1位の極をもち、留数は $1$ と求まる。
(1)の亜種として\begin{equation}\zeta(s)=-\frac{\G(1-s)}{2\pi i(1-2^{1-s})}\int_C\frac{(-z)^{s-1}}{e^z+1}dz\tag{2}\end{equation}
複素解析を用いたフルヴィッツゼータ関数の積分表示です。$C$ のハンケル路はガンマ関数のときにも何度か扱いました。
前回のおさらい
フルヴィッツゼータ関数 $\zeta(s,a)$ は\begin{equation}\zeta(s,a)=\sum_{n=0}^\infty\frac{1}{(n+a)^s}\quad(\mathfrak{R}s>1)\tag{3}\end{equation}と定義されます。フルヴィッツゼータ関数とリーマンゼータ関数の関係は明らかに $\zeta(s,1)=\zeta(s)$ です。本稿はリーマンゼータ関数の積分表示も兼ねています。
前回の話では、フルヴィッツゼータ関数は以下の表示をもつことを示しました。\begin{equation}\zeta(s,a)=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}e^{-ax}}{1-e^{-x}}dx\tag{4}\end{equation}
偏角と経路
$\mathfrak{R}s>1$ とします。積分$$\int_C\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz$$を考えます。経路 $C$ は下図です。

ハンケル路の取り扱いはガンマ関数のときに説明した記事が役立ちます:
被積分関数が $(-z)^{s-1}$ を含んでいるので $0$ が分岐点であることから、ハンケル路 $C$ では実軸の正の部分を横断するのを避けています。
なお $s$ が整数のときは分岐点とはなりませんので、$C_1$ と $C_3$ で積分は相殺され、閉じた小さな円 $C_2$ のみが値に寄与します。この場合について詳細は次回の記事とします。
被積分関数を見ると $z$ そのものよりも $-z$ を考えた方がいいです。そこで $-z$ 平面を可視化しました(下図)。
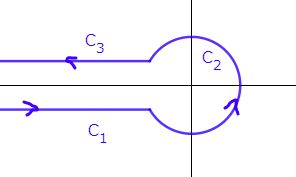
図から分かるように、偏角はまず $\arg(-z)=-\pi$ からスタートして $C_2$ を描きながら偏角は増加します。最後は $\arg(-z)=\pi$ となって $C_3$ を進んでいきます。
直線上の積分
したがって $C_1$ においては $-z=re^{-i\pi}$ として\begin{eqnarray*}\int_{C_1}\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz&=&\int_{\infty}^0\frac{(re^{-i\pi})^{s-1}e^{-ar}}{1-e^{-r}}(-e^{-i\pi}dr)\\&=&\int_{0}^\infty\frac{r^{s-1}e^{-i\pi s}e^{-ar}}{1-e^{-r}}dr\\&=&e^{-i\pi s}\int_{0}^\infty\frac{r^{s-1}e^{-ar}}{1-e^{-r}}dr\\&=&e^{-i\pi s}\G(s)\zeta(s,a)\quad(\because(4))\end{eqnarray*}
同様に $C_3$ においては $-z=re^{i\pi}$ として\begin{eqnarray*}\int_{C_3}\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz&=&\int_0^{\infty}\frac{(re^{i\pi})^{s-1}e^{-ar}}{1-e^{-r}}(-e^{i\pi}dr)\\&=&-\int_0^{\infty}\frac{r^{s-1}e^{i\pi s}e^{-ar}}{1-e^{-r}}dr\\&=&-e^{i\pi s}\int_{0}^\infty\frac{r^{s-1}e^{-ar}}{1-e^{-r}}dr\\&=&-e^{i\pi s}\G(s)\zeta(s,a)\quad(\because(4))\end{eqnarray*}
円弧の積分
$C_2$においては $-z=\epsilon e^{i\t}$ として偏角 $\t$ を $-\pi$ から $\pi$ へ変化させます。\begin{eqnarray*}\left|\int_{C_2}\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz\right|&=&\left|\int_{-\pi}^\pi\frac{(\epsilon e^{i\t})^{s-1}e^{a\epsilon e^{i\t}}}{1-e^{\epsilon e^{i\t}}}(-i\epsilon e^{i\t}d\t)\right|\\&\le&\epsilon^{\mathfrak{R}s}\int_{-\pi}^\pi\left|\frac{(e^{is\t})e^{a\epsilon e^{i\t}}}{1-e^{\epsilon e^{i\t}}}\right|d\t\\&=&\epsilon^{\mathfrak{R}s}\int_{-\pi}^\pi\left|\frac{e^{-\t\mathfrak{I}s}e^{a\epsilon\cos\t}}{1-e^{\epsilon e^{i\t}}}\right|d\t\\&=&\epsilon^{\mathfrak{R}s-1}\int_{-\pi}^\pi\left|e^{-\t\mathfrak{I}s}e^{a\epsilon\cos\t}\right|\left|\frac{\epsilon e^{i\t}}{1-e^{\epsilon e^{i\t}}}\right|d\t\end{eqnarray*}
$\left|\frac{\epsilon e^{i\t}}{1-e^{\epsilon e^{i\t}}}\right|$ は $\epsilon\to0$ で $1$ に収束するので有界です。さらに $e^{-\t\mathfrak{I}s}$ も $\t$ の積分範囲内で有界です。よって上界 $M$ が存在して\begin{eqnarray*}\left|\int_{C_2}\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz\right|&\le&M\epsilon^{\mathfrak{R}s-1}\int_{-\pi}^\pi\left|e^{a\epsilon\cos\t}\right|d\t\\&=&M\epsilon^{\mathfrak{R}s-1}\int_{-\pi}^\pi e^{a\epsilon\cos\t}d\t\\&=&2M\epsilon^{\mathfrak{R}s-1}\int_0^\pi e^{a\epsilon\cos\t}d\t\\&\le&2M\epsilon^{\mathfrak{R}s-1}e^{a\epsilon}\\&&\xrightarrow[\epsilon\to0]{}0\quad(\because\mathfrak{R}s>1)\end{eqnarray*}
この評価については以下の記事を参考にしました(外部リンク):
積分表示の導出
以上より、ハンケル積分路 $C=C_1+C_2+C_3$ 全体では$$\int_C\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz=(e^{-i\pi s}-e^{i\pi s})\G(s)\zeta(s,a)$$ここで$$e^{-i\pi s}-e^{i\pi s}=-2i\sin\pi s$$より$$\int_C\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz=-2i\sin\pi s\G(s)\zeta(s,a)$$ガンマ関数の相反公式$$\G(s)\G(1-s)=\frac{\pi}{\sin\pi s}$$を用いれば
\begin{equation}\zeta(s,a)=-\frac{\G(1-s)}{2\pi i}\int_C\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz\tag{5}\end{equation}
導出過程では $\mathfrak{R}s>1$ を仮定していましたが、(5)の右辺の積分はあらゆる $s$ で値をとります。しかし $\G(1-s)$ は $s=1,2,3\cdots$ で特異点を持ちます。よって(5)式は $s\neq 1,2,3\cdots$ に対して $\zeta(s,a)$ の値を与えます。なお $s=0,-1,-2\cdots$ に関しては、被積分関数は正則ではありませんが、留数定理により積分値が求まります(次回に詳述)ので(5)で定義できています。
一方 $s=2,3,4\cdots$ に対しては(5)では計算できませんが、フルヴィッツゼータ関数の定義式または前回の積分表示$$\zeta(s,a)=\sum_{n=0}^\infty\frac{1}{(n+a)^s}=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}e^{-ax}}{1-e^{-x}}dx$$を使えば値が得られるのでした。
以上から 特異点 $s=1$ を除いて $\zeta(s,a)$ を解析接続できました!
ガンマ関数の相反公式に関する詳細は:
ガンマ関数の極
$\zeta(s,a)$ を $s=1$ 以外で定義することができました。$s=1$ は特異点となります(発散する)。その原因は $\G(1-s)$ にあります。
「ガンマ関数の基礎」シリーズで $\G(z)$ は $z=0,-1,-2\cdots$ で1位の極をもつことを示しました。
つまり(5)の右辺 $\G(1-s)$ が極をもつせいで $s=1$ が $\zeta(s,a)$ の特異点となってしまうわけです。
ゼータ関数の極
(5)式を変形すると$$\frac{\zeta(s,a)}{\G(1-s)}=-\frac{1}{2\pi i}\int_C\frac{(-z)^{s-1}e^{-az}}{1-e^{-z}}dz$$右辺で $s=1$ とすれば$$-\frac{1}{2\pi i}\int_C\frac{e^{-az}}{1-e^{-z}}dz$$分岐点はありませんので $C_1$ と $C_3$ は同一の偏角としてよく、相殺します。さらに $C_2$ は原点中心の小さな閉じた円(時計回り)となるので\begin{eqnarray*}-\frac{1}{2\pi i}\int_C\frac{e^{-az}}{1-e^{-z}}dz&=&\mathrm{Res}_{z=0}\frac{e^{-az}}{1-e^{-z}}\\&=&\displaystyle\lim_{z\to0}\frac{ze^{-az}}{1-e^{-z}}\\&=&\displaystyle\lim_{z\to0}\frac{ze^{-az}}{1-e^{-z}}\\&=&\displaystyle\lim_{z\to0}\frac{-z-0}{e^{-z}-1}e^{-az}\\&=&-1\end{eqnarray*}
\begin{equation}\therefore\quad\displaystyle\lim_{s\to1}\frac{\zeta(s,a)}{\G(1-s)}=-1\tag{6}\end{equation}
$\G(1-s)$ は $s=1$ で1位の極をもつのでした。よって(6)より $\zeta(s,a)$ も $s=1$ に1位の極をもちます。
ゼータ関数の留数
その極における留数は\begin{eqnarray*}\displaystyle\lim_{s\to1}(s-1)\zeta(s,a)&=&\displaystyle\lim_{s\to1}(s-1)\G(1-s)\frac{\zeta(s,a)}{\G(1-s)}\\&=&-\displaystyle\lim_{s\to1}\G(2-s)\frac{\zeta(s,a)}{\G(1-s)}\\&=&1\quad(\because(6))\end{eqnarray*}
以上からフルヴィッツゼータ関数の特異点に関して次の結論を得ます。
$\zeta(s,a)$ は $s=1$ を除く全平面に解析接続される。また $s=1$ に1位の極をもち、その留数は $1$ である。
$$\zeta(s)=-\frac{\G(1-s)}{2\pi i(1-2^{1-s})}\int_C\frac{(-z)^{s-1}}{e^z+1}dz$$を示せ。$C$ はハンケル積分路である。またこの式を計算して $\zeta(0)$ を求めよ。
$$\int_C\frac{(-z)^{s-1}}{e^z+1}dz$$を考えます。先ほどと同様に $-z$ を置換します。\begin{eqnarray*}\int_{C_1}\frac{(-z)^{s-1}}{e^z+1}dz&=&-\int_\infty^0\frac{r^{s-1}e^{-i\pi s}}{e^r+1}dr\\&=&e^{-i\pi s}\int_0^\infty\frac{r^{s-1}}{e^r+1}dr\end{eqnarray*}\begin{eqnarray*}\int_{C_3}\frac{(-z)^{s-1}}{e^z+1}dz&=&-\int_0^\infty\frac{r^{s-1}e^{i\pi s}}{e^r+1}dr\\&=&-e^{i\pi s}\int_0^\infty\frac{r^{s-1}}{e^r+1}dr\end{eqnarray*}$$\int_{C_2}\frac{(-z)^{s-1}}{e^z+1}dz\xrightarrow[]{\epsilon\to0}0$$したがって$$\int_C\frac{(-z)^{s-1}}{e^z+1}dz=-2i\sin\pi s\int_0^\infty\frac{x^{s-1}}{e^x+1}dx$$前回の記事の類題によれば$$(1-2^{1-s})\zeta(s)=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}}{e^x+1}dx\quad(\mathfrak{R}s>0)$$でしたから$$\int_C\frac{(-z)^{s-1}}{e^z+1}dz=-2i\sin\pi s\G(s)(1-2^{1-s})\zeta(s)$$ガンマ関数の相反公式により$$\zeta(s)=-\frac{\G(1-s)}{2\pi i(1-2^{1-s})}\int_C\frac{(-z)^{s-1}}{e^z+1}dz$$
$s=0$ とすると$$\zeta(0)=\frac{-1}{2\pi i}\int_C\frac{dz}{z(e^z+1)}$$$C_1$ と $C_3$ は相殺しますので小さな円 $C_2$ のみが残り$$\zeta(0)=\frac{-1}{2\pi i}\int_{C_2}\frac{dz}{z(e^z+1)}$$被積分関数は $C_2$ 内の $z=0$ で1位の極をもちますから$$\zeta(0)=-\displaystyle\lim_{z\to0}\frac{1}{e^z+1}=-\frac{1}{2}$$これはよく知られた値ですね。似た方法で $\zeta(0,a)$ も求めることができます。
次回は実際に複素積分を計算してみます:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。







