本題に入る前に,2次元バージョンを確認しておきましょう.詳細は過去記事
 【H6】ベクトルの極座標成分
【H6】ベクトルの極座標成分
を参照ください.
任意の2次元ベクトルは一次独立な2つの基底ベクトルの組で表されます.以後,基底は単位ベクトルに限ることにしましょう.
最も簡単な基底は $\bm{e}_x=(1,0)$ と $\bm{e}_y=(0,1)$ の組です.しかし極座標成分を基底とすることもあります.下図のように物体の位置 $\bm{r}$ に平行な(動径方向という)単位ベクトル $\bm{e}_r$ と,それを90度だけ反時計回りに回転させた(角度方向という)$\bm{e}_\t$ を基底とするのです.
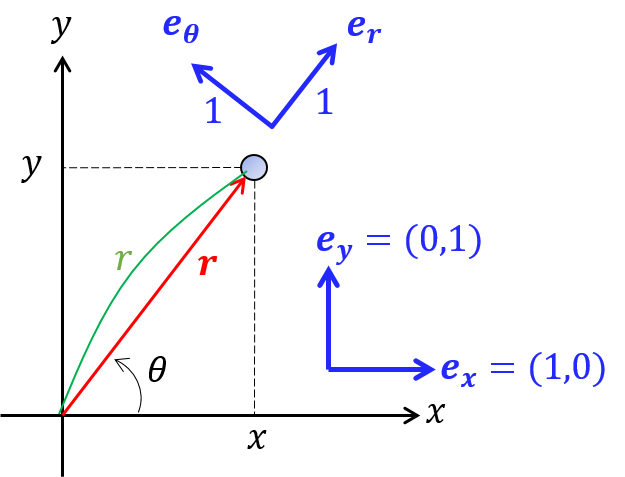
これらの基底は$$\begin{cases}\bm{e}_r& =&(\cos\t,\sin\t)\\\bm{e}_\t &=&(-\sin\t,\cos\t)\end{cases}$$と明示できます.
任意のベクトルは基底の線型結合で表せるので\begin{eqnarray*}\bm{F}&=&F_r\bm{e}_r+F_\t\bm{e}_\t\\\bm{v}&=&v_r\bm{e}_r+v_\t\bm{e}_\t\end{eqnarray*}のように書くことができます.
3次元極座標(球座標)では下図のように基底 $\bm{e}_r$ , $\bm{e}_\t$ , $\bm{e}_\phi$ をとります.
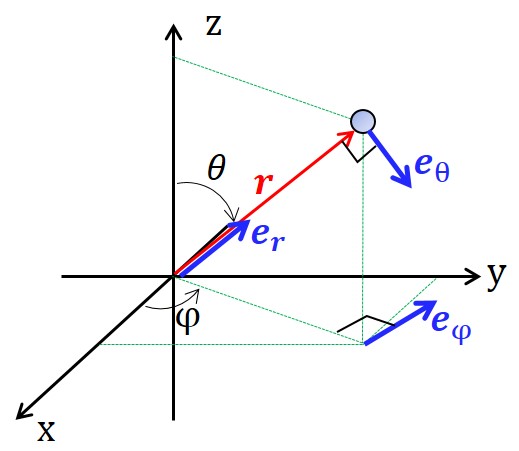
質点の位置 $\bm{r}$ と同じ方向の単位ベクトルが $\bm{e}_r$ です.直交座標 $(x,y,z)$ から球座標 $(r,\t,\phi)$ への変換は$$\begin{cases}x&=&r\sin\t\cos\phi\\y&=&r\sin\t\sin\phi\\z&=&r\cos\t\end{cases}$$ですので,原点からの距離 $r$ で割れば\begin{equation}\bm{e}_r=\begin{pmatrix}\sin\t\cos\phi\\\sin\t\sin\phi\\\cos\t\end{pmatrix}\tag{1}\end{equation}次に $\bm{e}_\t$ は「$\t$ が増加する方向」の単位ベクトルです.図1より $\bm{e}_\t$ は $\bm{e}_r$ の $\t$ を $\t+\frac{\pi}{2}$ としたものであると分かります($\bm{e}_\t$ は $\bm{r}$ と $z$ 軸を含む平面上にあります).ゆえに\begin{equation}\bm{e}_\t=\begin{pmatrix}\cos\t\cos\phi\\\cos\t\sin\phi\\-\sin\t\end{pmatrix}\tag{2}\end{equation}最後に $\bm{e}_\phi$ は $xy$ 平面の極座標の角度方向と同じなので\begin{equation}\bm{e}_\phi=\begin{pmatrix}-\sin\phi\\\cos\phi\\0\end{pmatrix}\tag{3}\end{equation}
(1)(2)(3)から $\bm{e}_r$ , $\bm{e}_\t$ , $\bm{e}_\phi$ は正規直交基底であることを示せ.ただし正規直交基底とは,基底どうしが直交し,かつ大きさが $1$ であるということ.
図1から基底を(1)(2)(3)のように導出しましたが,計算で実際に確認することは大事です.$$\bm{e}_r\cdot\bm{e}_r=\bm{e}_\t\cdot\bm{e}_\t=\bm{e}_\phi\cdot\bm{e}_\phi=1$$$$\bm{e}_r\cdot\bm{e}_\t=\bm{e}_\t\cdot\bm{e}_\phi=\bm{e}_\phi\cdot\bm{e}_r=0$$となることを確認しましょう.
質点の位置は刻々と変わるのが普通ですから,$\bm{r}$ は時間の関数です.よって $\bm{e}_r$ も時間の関数で,同時に $\bm{e}_\t$ , $\bm{e}_\phi$ も時間の関数であると分かります.
ということで基底ベクトルの時間微分をやってみましょう.(1)(2)(3)を微分します.$$\dot{\bm{e}_r}=\dot{\t}\begin{pmatrix}\cos\t\cos\phi\\\cos\t\sin\phi\\-\sin\t\end{pmatrix}+\dot{\phi}\begin{pmatrix}-\sin\t\sin\phi\\\sin\t\cos\phi\\0\end{pmatrix}$$\begin{equation}\therefore\quad\dot{\bm{e}_r}=\dot{\theta}\bm{e}_\t+\dot{\phi}\sin\t\bm{e}_\phi\tag{4}\end{equation}
$$\dot{\bm{e}_\t}=\dot{\t}\begin{pmatrix}-\sin\t\cos\phi\\-\sin\t\sin\phi\\-\cos\t\end{pmatrix}+\dot{\phi}\begin{pmatrix}-\cos\t\sin\phi\\\cos\t\cos\phi\\0\end{pmatrix}$$\begin{equation}\therefore\quad\dot{\bm{e}_\t}=-\dot{\theta}\bm{e}_r+\dot{\phi}\cos\t\bm{e}_\phi\tag{5}\end{equation}
$$\dot{\bm{e}_\phi}=-\dot{\phi}\begin{pmatrix}\cos\phi\\\sin\phi\\0\end{pmatrix}$$\begin{equation}\therefore\quad\dot{\bm{e}_\phi}=-\dot{\phi}(\sin\t\bm{e}_r+\cos\t\bm{e}_\t)\tag{6}\end{equation}
ここまでをまとめると
\begin{equation}\bm{e}_r=\begin{pmatrix}\sin\t\cos\phi\\\sin\t\sin\phi\\\cos\t\end{pmatrix}\tag{1}\end{equation}\begin{equation}\bm{e}_\t=\begin{pmatrix}\cos\t\cos\phi\\\cos\t\sin\phi\\-\sin\t\end{pmatrix}\tag{2}\end{equation}\begin{equation}\bm{e}_\phi=\begin{pmatrix}-\sin\phi\\\cos\phi\\0\end{pmatrix}\tag{3}\end{equation}
\begin{equation}\dot{\bm{e}_r}=\dot{\theta}\bm{e}_\t+\dot{\phi}\sin\t\bm{e}_\phi\tag{4}\end{equation}\begin{equation}\dot{\bm{e}_\t}=-\dot{\theta}\bm{e}_r+\dot{\phi}\cos\t\bm{e}_\phi\tag{5}\end{equation}\begin{equation}\dot{\bm{e}_\phi}=-\dot{\phi}(\sin\t\bm{e}_r+\cos\t\bm{e}_\t)\tag{6}\end{equation}
質点の位置は$$\bm{r}=r\bm{e}_r$$これを微分すると速度になります.$$\bm{v}=\dot{r}\bm{e}_r+r\dot{\bm{e}_r}$$(4)より$$\bm{v}=\dot{r}\bm{e}_r+r\dot{\theta}\bm{e}_\t+r\dot{\phi}\sin\t\bm{e}_\phi$$のように速度を球座標成分で書くことができます.
加速度は速度の微分ですから$$\bm{a}=\frac{d}{dt}\left(\dot{r}\bm{e}_r+r\dot{\theta}\bm{e}_\t+r\dot{\phi}\sin\t\bm{e}_\phi\right)$$計算すると\begin{eqnarray*}\bm{a}=&&(\ddot{r}-r\dot{\t}^2-r\dot{\phi}^2\sin^2\t)\bm{e}_r+(2\dot{r}\dot{\t}+r\ddot{\t}-r\dot{\phi}^2\sin\t\cos\t)\bm{e}_\t\\&+&(2\dot{r}\dot{\phi}\sin\t+2r\dot{\t}\dot{\phi}\cos\t+r\ddot{\phi}\sin\t)\bm{e}_\phi\end{eqnarray*}となります.
長さ $l$ の糸でつくられた振り子がある.糸の片端は質量 $m$ , 位置 $\bm{r}$ の質点に,もう片端は原点に固定されている.糸は常にピンと張っている状態であり,糸の張力の大きさを $S(t)$ とすると質点にかかる力は$$\bm{F}=-S(t)\bm{e}_r+mg\bm{e}_z$$である.このときの運動方程式を球座標成分ごとに立て,$\dot{\phi}\sin^2\t$ が保存することを示せ.なお $z$ 軸が鉛直下向きになるよう座標を設定している.
z方向の単位ベクトルは球座標の基底に直す必要があります.$$\bm{e}_z=\begin{pmatrix}0\\0\\1\end{pmatrix}=\cos\t\bm{e}_r-\sin\t\bm{e}_\t$$$$\therefore\quad\bm{F}=(mg\cos\t-S(t))\bm{e}_r-mg\sin\t\bm{e}_\t+0\bm{e}_\phi$$$r=l$(定数)であることに注意すると,加速度は$$\bm{a}=-l(\dot{\t}^2+\dot{\phi}^2\sin^2\t)\bm{e}_r+l(\ddot{\t}-\dot{\phi}^2\sin\t\cos\t)\bm{e}_\t\\+l(2\dot{\t}\dot{\phi}\cos\t+\ddot{\phi}\sin\t)\bm{e}_\phi$$$\bm{F}=m\bm{a}$ として係数を比較することにより\begin{eqnarray*}&mg\cos\t-S(t)=-ml(\dot{\t}^2+\dot{\phi}^2\sin^2\t)\\&-g\sin\t=l(\ddot{\t}-\dot{\phi}^2\sin\t\cos\t)\\&0=2\dot{\t}\dot{\phi}\cos\t+\ddot{\phi}\sin\t\end{eqnarray*}これが球座標成分ごとの運動方程式である.最下段の式に $\sin\t$ をかけると$$2\dot{\t}\dot{\phi}\cos\t\sin\t+\ddot{\phi}\sin^2\t=0$$$$\therefore\quad\frac{d}{dt}\left(\dot{\phi}\sin^2\t\right)=0$$よって $\dot{\phi}\sin^2\t$ は保存する.
任意のベクトルは3つの基底の線型結合で表せます.基底を取り換えればベクトル成分も当然変換されます.
例えばベクトル $\bm{A}$ は直交座標表示で $$\bm{A}=A_x\bm{e}_x+A_y\bm{e}_y+A_z\bm{e}_z$$このときのベクトル成分は $(A_x,A_y,A_z)$ です.
一方球座標表示では$$\bm{A}=A_r\bm{e}_r+A_\t\bm{e}_\t+A_\phi\bm{e}_\phi$$このときのベクトル成分は $(A_r,A_\t,A_\phi)$ です.両式とも同じ $\bm{A}$ ですから$$A_r\bm{e}_r+A_\t\bm{e}_\t+A_\phi\bm{e}_\phi=A_x\bm{e}_x+A_y\bm{e}_y+A_z\bm{e}_z$$(1)(2)(3)によって左辺を変形すると\begin{eqnarray*}A_r\bm{e}_r+A_\t\bm{e}_\t+A_\phi\bm{e}_\phi&=&(A_r\sin\t\cos\phi+A_\t\cos\t\cos\phi-A_\phi\sin\phi)\bm{e}_x\\&&+(A_r\sin\t\sin\phi+A_\t\cos\t\sin\phi+A_\phi\cos\phi)\bm{e}_y\\&&+(A_r\cos\t-A_\t\sin\t)\bm{e}_z\end{eqnarray*}$$\therefore\quad\begin{cases}A_x&=&A_r\sin\t\cos\phi+A_\t\cos\t\cos\phi-A_\phi\sin\phi\\A_y&=&A_r\sin\t\sin\phi+A_\t\cos\t\sin\phi+A_\phi\cos\phi\\A_z&=&A_r\cos\t-A_\t\sin\t\end{cases}$$この変換を行列で表現すると$$\begin{pmatrix}A_x\\A_y\\A_z\end{pmatrix}=\begin{pmatrix}\sin\t\cos\phi & \cos\t\cos\phi & -\sin\phi \\ \sin\t\sin\phi & \cos\t\sin\phi & \cos\phi \\ \cos\t & -\sin\t & 0\end{pmatrix}\begin{pmatrix}A_r\\A_\t\\A_\phi\end{pmatrix}$$逆行列を求めることにより,逆変換は$$\begin{pmatrix}A_r\\A_\t\\A_\phi\end{pmatrix}=\begin{pmatrix}\sin\t\cos\phi & \sin\t\sin\phi & \cos\t \\ \cos\t\cos\phi & \cos\t\sin\phi & -\sin\t \\ -\sin\phi & \cos\phi & 0\end{pmatrix}\begin{pmatrix}A_x\\A_y\\A_z\end{pmatrix}$$
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。