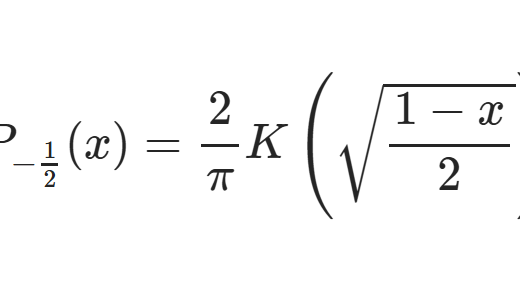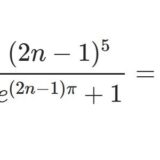今回からルジャンドル関数の話をしていきます。過去にもルジャンドル関数に関する記事を単発的に書いていますので、それらも活用していきます。
特殊関数の記事一覧はこちらから:
もくじ
ルジャンドル多項式の定義にはいくつか流儀があります。過去記事ではルジャンドルの微分方程式の解として定義をしました。本シリーズではある関数の展開式であらわれる多項式として定義します。
簡単な多項式
$h$ の関数として\begin{equation}f(h):=(1-2zh+h^2)^{-1/2}\tag{1}\end{equation}を考えます。(1)は $(1-X)^{-1/2}$ の形をしており $|2zh-h^2|<1$ なら収束して $2zh-h^2$ で展開できます。さらに $|2zh|+|h|^2<1$ なら絶対収束するので好きに並べ替えることができます。つまり $h$ の昇冪で表せます。
マクローリン展開の基礎的な式\begin{equation}(1-X)^{-1/2}=\sum_{n=0}^\infty \frac{(2n-1)!!}{(2n)!!}X^n\tag{2}\end{equation}を(1)に適用して $h$ の展開式として整理すると$$f(h)=1+zh+\frac{3z^2-1}{2}h^2+\frac{5z^3-3z}{2}h^3+\cdots$$ここに $n$ 次係数として表れている $z$ の多項式を、$n$ 次のルジャンドル多項式といい $P_n(z)$ と書きます。すなわち\begin{equation}f(h)=P_0(z)+P_1(z)h+P_2(z)h^2+P_3(z)h^3+\cdots\tag{3}\end{equation}比較することで\begin{align}P_0(z) &= 1\\P_1(z)&=z\\ P_2(z) &=\frac{3z^2-1}{2}\\ P_3(z) &=\frac{5z^3-3z}{2}\end{align}のようになります。
一般のルジャンドル多項式
では一般に $n$ 次のルジャンドル多項式はどのようになるでしょうか。まず\begin{equation}f(h)=\sum_{n=0}^\infty \frac{(2n-1)!!}{(2n)!!}(2zh-h^2)^n\tag{4}\end{equation}に二項定理を用いて$$f(h)=\sum_{n=0}^\infty \sum_{r=0}^n\frac{(2n-1)!!}{(2n)!!}\binom{n}{r}(2z)^{n-r}h^{n+r}$$簡単のために\begin{equation}a_{n,r}:=\frac{(2n-1)!!}{(2n)!!}\binom{n}{r}(2z)^{n-r}\tag{5}\end{equation}とおいておくと\begin{equation}f(h)=\sum_{n=0}^\infty \sum_{r=0}^n a_{n,r}h^{n+r}\tag{6}\end{equation}
さて(6)を $h$ の昇冪に整理しなければなりません。最初の数項を書き出すと$$f(h)=a_{0,0}+a_{1,0}h+(a_{2,0}+a_{1,1})h^2+(a_{3,0}+a_{2,1})h^3+(a_{4,0}+a_{3,1}+a_{2,2})h^4+\cdots$$のように整理されればよいのです。したがって\begin{align}f(h) &=a_{0,0}+a_{1,0}h+(a_{2,0}+a_{1,1})h^2+(a_{3,0}+a_{2,1})h^3+\cdots \\&=\sum_{n=0}^\infty\left( \sum_{m=0}^{\lfloor \frac{n}{2}\rfloor}a_{n-m,m}\right)h^n\end{align}(5)より\begin{align}f(h)&=\sum_{n=0}^\infty\left( \sum_{m=0}^{\lfloor \frac{n}{2}\rfloor}\frac{(2n-2m-1)!!}{(2n-2m)!!}\binom{n-m}{m}(2z)^{n-2m}\right)h^n\\&=\sum_{n=0}^\infty\left( \sum_{m=0}^{\lfloor \frac{n}{2}\rfloor}\frac{(2n-2m-1)!!}{(2n-2m)!!}\frac{(n-m)!}{m!(n-2m)!}(2z)^{n-2m}\right)h^n\\&=\sum_{n=0}^\infty\left( \sum_{m=0}^{\lfloor \frac{n}{2}\rfloor}\frac{(2n-2m-1)!!}{(2n-2m)!!}\frac{(2n-2m)!!}{(2m)!!(n-2m)!}z^{n-2m}\right)h^n\\&=\sum_{n=0}^\infty\left( \sum_{m=0}^{\lfloor \frac{n}{2}\rfloor}\frac{(2n-2m)!}{(2n-2m)!!}\frac{1}{(2m)!!(n-2m)!}z^{n-2m}\right)h^n\\ &=\sum_{n=0}^\infty\left( \sum_{m=0}^{\lfloor \frac{n}{2}\rfloor}\frac{(2n-2m)!}{2^nm!(n-m)!(n-2m)!}z^{n-2m}\right)h^n\end{align}したがって次の結論を得ます。
$n$ 次のルジャンドル多項式 $P_n(z)$ は$$P_n(z)=\sum_{m=0}^{\lfloor \frac{n}{2}\rfloor}\frac{(2n-2m)!}{2^nm!(n-m)!(n-2m)!}z^{n-2m}$$
定理1に $z=1$ を代入すると\begin{equation}P_n(1)=\sum_{m=0}^{\lfloor \frac{n}{2}\rfloor}\frac{(2n-2m)!}{2^nm!(n-m)!(n-2m)!}\tag{7}\end{equation}これを直接計算するのは骨が折れそうですが、(1)に立ち返って考えてみると $z=1$ として$$(1-2h+h^2)^{-1/2}=\frac{1}{1-h}=1+h+h^2+\cdots$$です。同様に$z=-1$ ならば$$(1+2h+h^2)^{-1/2}=\frac{1}{1+h}=1-h+h^2-\cdots$$よって\begin{equation}P_n(1)=1\;,\quad P_n(-1)=(-1)^n\tag{8}\end{equation}
また $z=0$ とした場合は$$(1+h^2)^{-1/2}=\sum_{n=0}^\infty \frac{(2n-1)!!}{(2n)!!}(-h^2)^n$$と展開できるので\begin{equation}P_{2n+1}(0)=0\;,\quad P_{2n}(0)=\frac{(2n-1)!!}{(2n)!!}(-1)^n\tag{9}\end{equation}
実数 $\t$ に対して $z=\cos\t$ のとき(1)は\begin{align}(1-2h\cos\t+h^2)^{-1/2} &=(1-he^{i\t}-he^{-i\t}+h^2)^{-1/2}\\&=(1-he^{i\t})^{-1/2}(1-he^{-i\t})^{-1/2}\\ &=\left(\sum_{m=0}^\infty\frac{(2m-1)!!}{(2m)!!}e^{im\t}h^m\right) \left(\sum_{m=0}^\infty\frac{(2m-1)!!}{(2m)!!}e^{-im\t}h^m\right)\end{align}簡単のために$$a_m := \frac{(2m-1)!!}{(2m)!!}$$とおくことにすると$$(1-2h\cos\t+h^2)^{-1/2}=\left(\sum_{m=0}^\infty a_me^{im\t}h^m\right) \left(\sum_{m=0}^\infty a_me^{-im\t}h^m\right)$$コーシー積をとって$$=\sum_{n=0}^\infty\left(\sum_{m=0}^n a_ma_{n-m}e^{i(n-2m)\t}\right)h^n$$よって $h^n$ の係数は\begin{align}P_n(\cos\t) &=\sum_{m=0}^n a_ma_{n-m}e^{i(n-2m)\t} \\&=a_0a_ne^{in\t}+a_1a_{n-1}e^{i(n-2)\t}+\cdots +a_na_0e^{i(-n)\t}\\ &= 2a_0a_n\cos n\t+2a_1a_{n-1}\cos(n-2)\t+\cdots\end{align}最終行での「$\cdots$」の末項は $n$ の偶奇によって異なります。すなわち\begin{align}P_{2k}(\cos\t) &=2a_0a_{2k}\cos 2k\t+2a_1a_{2k-1}\cos(2k-2)\t+\cdots +2a_{k-1}a_{k+1}\cos2\t + a_k^{~2}\\P_{2k-1}(\cos\t) &= 2a_0a_{2k-1}\cos (2k-1)\t+2a_1a_{2k-2}\cos(2k-3)\t+\cdots +2a_{k-1}a_{k}\cos\t\end{align}偶奇のいずれにせよ、絶対値 $|P_n(\cos\t)|$ を三角不等式によって評価すれば、$\t=0$ とした場合と比較して$$|P_n(\cos\t)|\le P_n(1)$$(8)によって右辺は $1$ です。
$\t\in\RR$ ,$$|P_n(\cos\t)|\le 1$$
$$P_n(z)=\frac{1}{2^nn!}\frac{d^n}{dz^n}(z^2-1)^n$$
証明はこちらを参考にしてください。
$$P_n(z)=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^n}{2^n(t-z)^{n+1}}dt\quad(n\in\mathbb{Z^+})$$ただし $C$ は $z$ 回りを1周する小さな円.
証明はこちらをご覧ください。
ルジャンドル多項式 $P_n(z)$ は次の微分方程式の解である。$$(1-z^2)y^{\prime\prime}-2zy'+n(n+1)y=0$$または$$\frac{d}{dz}\left((1-z^2)\frac{dy}{dz}\right)+n(n+1)y=0$$
この微分方程式の解き方はこちらを参考にしてください。
定理5の微分方程式は $z=\pm 1$,$\infty$ に確定特異点を持つフックス型微分方程式です。変形すると\begin{equation}y''+\left(\frac{1}{z-1}+\frac{1}{z+1}\right)y'-\frac{n(n+1)}{(z-1)(z+1)}y=0\tag{10}\end{equation}となるので、リーマンのP方程式の形と比較すれば、特異点 $1$ に属する指数は $0,0$ , 特異点 $-1$ に属する指数は $0,0$ , 特異点 $\infty$ に属する指数は $-n,n+1$ となります。したがってこの微分方程式の解全体をリーマンのP記法で示すと\begin{equation}P\left\{\begin{matrix}1 & \infty & -1\\0 & -n & 0\\0 & n+1 & 0\end{matrix}\;z\right\}\tag{11}\end{equation}(11)の表記によって解を級数で表した時の様子が一目でわかります。
なお $z^2=w$ と変換して定理5を書き直すことによって、ルジャンドルの微分方程式は超幾何微分方程式に書き直せることがわかります。
ルジャンドル本人によって次の関係式が示されています。
$$\int_{-1}^1 P_m(z)P_n(z)dz=\begin{cases}0\quad &(m\neq n)\\\cfrac{2}{2n+1}\quad &(m=n)\end{cases}$$
これを示しましょう。定理3を使うと$$\int_{-1}^1 P_m(z)P_n(z)dz = \frac{1}{(2m)!!(2n)!!}\int_{-1}^1 \left(\frac{d^{m}}{dz^m}(z^2-1)^m\right)\left(\frac{d^{n}}{dz^n}(z^2-1)^n\right)dz$$となります。これを部分積分していきます。
自然数 $k$ に対して $(z^2-1)^k$ を考えます。これは因数として $z^2-1$を $k$ 個もっています。何度か微分してみるとわかるのですが、微分するたびに $z^2-1$ の数は1個ずつ減っていくのです。つまり $(z^2-1)^k$ の $k-1$ 階微分までは $z^2-1$ を因数に持つので、$z=\pm1$ を代入するとゼロになるということです。これを利用します。
繰り返し部分積分することにより\begin{align}\int_{-1}^1 P_m(z)P_n(z)dz &= \frac{1}{(2m)!!(2n)!!}\int_{-1}^1 \left(\frac{d^{m}}{dz^m}(z^2-1)^m\right)\left(\frac{d^{n}}{dz^n}(z^2-1)^n\right)dz\\&=\frac{(-1)}{(2m)!!(2n)!!}\int_{-1}^1 \left(\frac{d^{m-1}}{dz^{m-1}}(z^2-1)^m\right)\left(\frac{d^{n+1}}{dz^{n+1}}(z^2-1)^n\right)dz\\ &\vdots\\ &=\frac{(-1)^m}{(2m)!!(2n)!!}\int_{-1}^1 (z^2-1)^m\left(\frac{d^{m+n}}{dz^{m+n}}(z^2-1)^n\right)dz\end{align}ここで $m>n$ としましょう。$(z^2-1)^n$ は $2n$ 次式なので $2n$ 回を超えて微分するとゼロになります。したがって $m+n>2n$ より$$\int_{-1}^1 P_m(z)P_n(z)dz=0\quad (m> n)$$です。対称性から $n>m$ でも同じ結論になります。
次に $m=n$ のときは\begin{align}\int_{-1}^1 P_m(z)P_n(z)dz &=\frac{(-1)^n}{(2n)!!^2}\int_{-1}^1 (z^2-1)^n\left(\frac{d^{2n}}{dz^{2n}}(z^2-1)^n\right)dz\end{align}$(z^2-1)^n$ は $2n$ 次式なので最高次以外は微分によってゼロになり\begin{align}\int_{-1}^1 P_m(z)P_n(z)dz &=\frac{(-1)^n\: (2n)!}{(2n)!!^2}\int_{-1}^1 (z^2-1)^ndz\\&=\frac{(2n-1)!!}{(2n)!!}\int_{-1}^1 (1-z^2)^ndz\\&=\frac{(2n-1)!!}{(2n)!!}\cdot 2\int_{0}^\frac{\pi}{2} \cos^{2n+1}\t d\t\quad (z=\sin\t)\\&=2\frac{(2n-1)!!}{(2n)!!}\frac{(2n)!!}{(2n+1)!!}\\&=\frac{2}{2n+1}\end{align}以上で定理6が導かれました。
定理6の性質から $P_n(z)$ は直交性をもつといいます。特に $P_n(z)\sqrt{n+\dfrac{1}{2}}$ は積分区間 $[-1,1]$ で正規直交するといいます($m\neq n$ でゼロ、$m=n$ で1)。
$x>0$ とする。$$\int_{-1}^1\frac{P_n(z) dz}{\sqrt{\cosh 2x-z}}=\frac{2\sqrt{2}}{2n+1}e^{-(2n+1)x}$$を示せ。
$$\cosh 2x-z=\frac{e^{2x}}{2}(1-2xe^{-2x}+e^{-4x})$$より$$\left(\cosh 2x-z\right)^{-1/2}=\sqrt{2}e^{-x}\sum_{m=0}^\infty P_m(z)e^{-2mx}$$となる。あとは直交性を用いるとよい。
今回はルジャンドル多項式の定義と性質をざっと見ていきました。次回からはより一般の関数である「ルジャンドル関数」について解説していきます:
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。