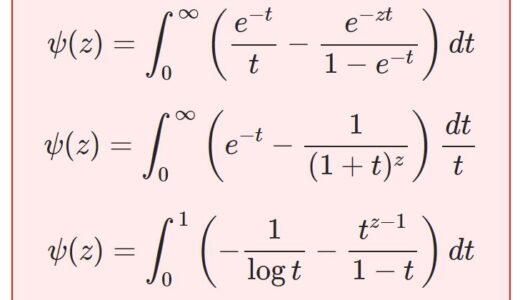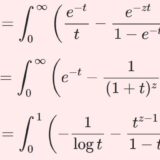「ガンマ関数の基礎」シリーズ第16回です。前回はディガンマ関数の積分表示をやりました:
そこで得た結果を少し使うのでよければ参考にしてください。
今回はビネ(Binet)の第1公式を導出します。
$\mathfrak{R}z>0$ として$$\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi+\int_0^\infty\left(\frac{1}{e^t-1}-\frac{1}{t}+\frac{1}{2}\right)e^{-zt}\frac{dt}{t}$$
実は以前、前提知識なしの導出方法を紹介しています(2本立て)。
Binetの第1公式の初等的証明(ログガンマの積分表示)前半
Binetの第1公式の初等的証明(ログガンマの積分表示)後半
なので改めてやる必要はないといえばないです。ただそのときの記事は本シリーズとは違う単発記事でした。ですので今回は「ガンマ関数の基礎」シリーズの流れの1つとして別の方法によって導いていきます(多少似ている)。おおまかな進め方はWhittaker&Watsonの12章を踏まえています。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
最近ガンマ関数の記事をひたすら書いています。それは私自身が今ガンマ関数の勉強をしているからで、そのアウトプットとして記事になっています。特に本記事も含め、ガンマ関数関連の積分表示の技巧には本当に驚かされます。ビネの公式はなかなか面倒くさいのですが、その技巧を味わうためにも是非しっかり読んでいただけたらと思います。
ガンマ関数 $\G(z)$ の対数をとって微分したものをディガンマ関数 $\psi(z)$ というのでした。つまり
\begin{equation}\psi(z)=\frac{d}{dz}\log\G(z)\tag{1}\end{equation}
ということです。
以下ずっと $\mathfrak{R}z>0$ でいきましょう。ディガンマ関数は次の積分表示をもちます。
\begin{equation}\psi(z)=\int_0^\infty\left(\frac{e^{-t}}{t}-\frac{e^{-zt}}{1-e^{-t}}\right)dt\tag{2}\end{equation}
あとで使います。
\begin{equation}\log z=\int_0^\infty \frac{e^{-t}-e^{-zt}}{t}dt\tag{3}\end{equation}
証明方法①
左辺を微分すると $\frac{1}{z}$ , 右辺を(順序交換を気にせず)微分すると$$\displaystyle\int_0^\infty e^{-zt}dt=\frac{1}{z}$$よって積分定数を $C$ として$$\log z+C=\int_0^\infty \frac{e^{-t}-e^{-zt}}{t}dt$$$z=1$ を代入すれば $C=0$ です。これでよし。
証明方法②
$$\int_\epsilon^R \frac{e^{-t}-e^{-zt}}{t}dt=\int_\epsilon^R \frac{e^{-t}}{t}dt-\int_{\epsilon z}^{Rz}\frac{e^{-t}}{t}dt$$

上図の経路を1周するとゼロとなることから$$\int_\epsilon^R \frac{e^{-t}}{t}dt-\int_{\epsilon z}^{Rz}\frac{e^{-t}}{t}dt=\int_\epsilon^{\epsilon z} \frac{e^{-t}}{t}dt-\int_{R}^{Rz}\frac{e^{-t}}{t}dt$$と区間を書き換えることができます。右辺第2項について$$\left|\int_{R}^{Rz}\frac{e^{-t}}{t}dt\right|=\left|\int_{1}^{z}\frac{e^{-Rs}}{s}ds\right|\xrightarrow[]{R\to\infty}0$$右辺第2項について\begin{eqnarray*}\int_\epsilon^{\epsilon z} \frac{e^{-t}}{t}dt&=&\int_\epsilon^{\epsilon z}\left(\frac{1}{t}-\frac{1-e^{-t}}{t}\right)dt\\&=&\log z-\int_\epsilon^{\epsilon z}\frac{1-e^{-t}}{t}dt\\&\rightarrow&\log z\quad(as\quad \epsilon\to0)\end{eqnarray*}$$\therefore\quad\log z=\int_0^\infty \frac{e^{-t}-e^{-zt}}{t}dt$$
巧みな組み換え
(2)より$$\psi(z+1)=\int_0^\infty\left(\frac{e^{-t}}{t}-\frac{e^{-zt}}{e^{t}-1}\right)dt$$ここで$$\frac{1}{2z}=\int_0^\infty\frac{1}{2}e^{-zt}dt$$および(3)により\begin{eqnarray*}\psi(z+1)&=&\int_0^\infty\left(\frac{e^{-t}}{t}-\frac{e^{-zt}}{e^{t}-1}\right)dt\\&=&\int_0^\infty\frac{1}{2}e^{-zt}dt+\int_0^\infty\frac{e^{-t}-e^{-zt}}{t}dt\\&&+\int_0^\infty\left(\frac{e^{-zt}}{t}-\frac{1}{2}e^{-zt}-\frac{e^{-zt}}{e^t-1}\right)dt\\&=&\frac{1}{2z}+\log z-\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)e^{-zt}dt\end{eqnarray*}よって
\begin{equation}\psi(z+1)=\frac{1}{2z}+\log z-\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)e^{-zt}dt\tag{4}\end{equation}
なかなか巧みな技ですね。
積分の収束
(4)の積分について見ていきましょう。$t=0$ で被積分関数は値をとりませんが\begin{eqnarray*}\displaystyle\lim_{t\to0}\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)&=&\frac{1}{2}\displaystyle\lim_{t\to0}\frac{(t-2)e^t+t+2}{t(e^t-1)}\\&=&\frac{1}{2}\displaystyle\lim_{t\to0}\frac{(t-1)e^t+1}{(t+1)e^t-1}\\&=&\frac{1}{2}\displaystyle\lim_{t\to0}\frac{te^t}{(t+2)e^t}\\&=& 0\end{eqnarray*}この式変形の1行目右辺の分子は、2回微分することで正であることが分かります。ゆえに $\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}>0$ です。また $e^t>1+t$ を用いれば $\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\le \frac{1}{2}$ と分かります。グラフではこんなかんじです。
$\mathfrak{R}z>0$ でしたので積分は収束します。
対数ガンマの登場
冒頭で述べたように$$\psi(z)=\frac{d}{dz}\log\G(z)$$ですから(4)は$$\frac{d}{dz}\log\G(z+1)=\frac{1}{2z}+\log z-\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)e^{-zt}dt$$と書けます。この両辺を $1$ から $z$ まで積分することを考えましょう。左辺は $\log\G(z+1)$ となります。右辺は$$\frac{1}{2}\log z+z\log z-z+1-\int_1^z\int_0^\infty\left[\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)e^{-zt}dt\right]dz$$積分については順序を交換して\begin{multline}\int_0^\infty\int_1^z\left[\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)e^{-zt}dz\right]dt\\=\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)(e^{-t}-e^{-zt})\frac{dt}{t}\end{multline}$$\therefore\quad\log\G(z+1)=\left(z+\frac{1}{2}\right)\log z-z+1+\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)\frac{e^{-zt}-e^{-t}}{t}dt$$$\G(z+1)=z\G(z)$ より
\begin{equation}\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+1+\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)\frac{e^{-zt}}{t}dt-\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)\frac{e^{-t}}{t}dt\tag{5}\end{equation}
とあらわせます。最後の定積分は次の方法で計算することができます。
\begin{equation}\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)\frac{e^{-t}}{t}dt=1-\frac{1}{2}\log2\pi\tag{6}\end{equation}
これを証明できればゴールです。今から示す方法はプリングスハイム(Alfred Pringsheim)が「Mathematische Annalen 31」という会誌で示したものです(1888年)。論文のタイトルを"Zur Theorie der Gamma-Functionen"といいます。なお有料なので私は原典には当たっていません。←無料の見つけました。でもドイツ語なので何も分かりませんでした。なので見出しのタイトルに「仮」と入れてあります。
さて $I,J$ を以下のように定義します。求めたいのは $I$ ですね。$$I\equiv\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)\frac{e^{-t}}{t}dt$$$$J\equiv\int_0^\infty\left(\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\right)\frac{e^{-\frac{t}{2}}}{t}dt$$(5)で $z=1/2$ とすると\begin{equation}\frac{1}{2}\log \pi=\frac{1}{2}+J-I\tag{7}\end{equation}$I$ について $t$ を $t/2$ と置換すると$$I=\int_0^\infty\left(\frac{1}{2}-\frac{2}{t}+\frac{1}{e^\frac{t}{2}-1}\right)\frac{e^{-\frac{t}{2}}}{t}dt$$なので $J$ の定義式と引き算すると\begin{eqnarray*}J-I&=&\int_0^\infty\left(\frac{1}{t}+\frac{1}{e^t-1}-\frac{1}{e^{\frac{t}{2}}-1}\right)\frac{e^{-\frac{t}{2}}}{t}dt\\&=&\int_0^\infty\left(\frac{e^{-\frac{t}{2}}}{t}+\frac{e^{-\frac{t}{2}}}{e^t-1}-\frac{e^{-\frac{t}{2}}}{e^{\frac{t}{2}}-1}\right)\frac{dt}{t}\\&=&\int_0^\infty\left(\frac{e^{-\frac{t}{2}}}{t}-\frac{1}{e^t-1}\right)\frac{dt}{t}\end{eqnarray*}
よって\begin{eqnarray*}J&=&(J-I)+I\\&=&\int_0^\infty\left(\frac{e^{-\frac{t}{2}}}{t}-\frac{1}{e^t-1}+\frac{e^{-t}}{2}-\frac{e^{-t}}{t}+\frac{e^{-t}}{e^t-1}\right)\frac{dt}{t}\\&=&\int_0^\infty\left(\frac{e^{-\frac{t}{2}}-e^{-t}}{t}-\frac{e^{-t}}{2}\right)\frac{dt}{t}\end{eqnarray*}となります。ここで$$-\frac{d}{dt}\left(\frac{e^{-\frac{t}{2}}-e^{-t}}{t}\right)=\frac{e^{-\frac{t}{2}}-e^{-t}}{t^2}+\frac{\frac{1}{2}e^{-\frac{t}{2}}-e^{-t}}{t}$$を用いると\begin{eqnarray*}J&=&\int_0^\infty\left[-\frac{d}{dt}\left(\frac{e^{-\frac{t}{2}}-e^{-t}}{t}\right)-\frac{\frac{1}{2}e^{-\frac{t}{2}}-e^{-t}}{t}-\frac{e^{-t}}{2t}\right]dt\\&=&-\left[\frac{e^{-\frac{t}{2}}-e^{-t}}{t}\right]_0^\infty+\frac{1}{2}\int_0^\infty\frac{e^{-t}-e^{-\frac{t}{2}}}{t}dt\\&=&-\left.\frac{e^{-\frac{t}{2}}-e^{-t}}{t}\right|_{t=0}+\frac{1}{2}\int_0^\infty\frac{e^{-t}-e^{-\frac{t}{2}}}{t}dt\end{eqnarray*}
第1項については平均値の定理を区間 $[\frac{t}{2},t]$ で用いて$$\displaystyle\lim_{t\to0}\frac{e^{-\frac{t}{2}}-e^{-t}}{t}=-\frac{1}{2}\lim_{t\to0}\frac{e^{-\frac{t}{2}}-e^{-t}}{\frac{t}{2}-t}=\frac{1}{2}\displaystyle\lim_{c\to0}e^c=\frac{1}{2}$$第2項については(3)を用いればOKです。ゆえに$$J=\frac{1}{2}-\frac{1}{2}\log2$$これを(7)に代入すると$$I=1-\frac{1}{2}\log2\pi$$これで(6)は示されました。
(6)を(5)に適用することでついにビネの第1公式が示されました。
$$\log\G(z)=\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi+\int_0^\infty\left(\frac{1}{e^t-1}-\frac{1}{t}+\frac{1}{2}\right)e^{-zt}\frac{dt}{t}$$
$z$ を実数とすると、積分の項は $1/z$ のオーダーなので $z$ が大きいときには無視できます。ゆえに$$\log\G(z)\approx\left(z-\frac{1}{2}\right)\log z-z+\frac{1}{2}\log2\pi$$なる近似ができます。
次回はKummerの公式を導出します。
Binetの第1公式の別の導出はこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。