「ガンマ関数の基礎」シリーズ第15回です。前回はオイラー・マスケローニ定数の積分表示を導出しました:
【γ14】オイラー定数の積分表示2選・調和数・積分評価(ガンマ関数の基礎14)
一応、本記事の前提知識となります。
$\mathfrak{R}z>0$ とすると$$\psi(z)=\int_0^\infty\left(\frac{e^{-t}}{t}-\frac{e^{-zt}}{1-e^{-t}}\right)dt$$$$\psi(z)=\int_{0}^\infty\left(e^{-t}-\frac{1}{(1+t)^z}\right)\frac{dt}{t}$$$$\psi(z)=\int_0^1\left(-\frac{1}{\log t}-\frac{t^{z-1}}{1-t}\right)dt$$
ガンマ関数の対数をとって微分したものを「ディガンマ関数 $\psi(z)$」といいます。今日はこの級数表示がスタートとなります。
\begin{equation}\psi(z)=-\g-\sum_{n=0}^\infty\left(\frac{1}{z+n}-\frac{1}{n+1}\right)\tag{1}\end{equation}
$\g$ はオイラー定数です。この導出については:
を参照ください。
巧妙に積分化
$$\frac{1}{a}=\int_0^\infty e^{-at}dt\quad(a>0)$$を(1)に用いて\begin{eqnarray*}\psi(z)&=&-\g-\sum_{n=0}^\infty\left(\frac{1}{z+n}-\frac{1}{n+1}\right)\\&=&-\g-\frac{1}{z}+\displaystyle\lim_{n\to\infty}\sum_{k=1}^n\left(\frac{1}{k}-\frac{1}{z+k}\right)\\&=&-\g-\int_0^\infty e^{-zt}dt+\displaystyle\lim_{n\to\infty}\sum_{k=1}^n\int_0^\infty\left(e^{-kt}-e^{-(k+z)t}\right)dt\\&=&-\g-\int_0^\infty e^{-zt}dt+\displaystyle\lim_{n\to\infty}\int_0^\infty\left(\sum_{k=1}^ne^{-kt}-\sum_{k=1}^ne^{-(k+z)t}\right)dt\end{eqnarray*}シグマのところは等比数列の和ですから\begin{eqnarray*}\psi(z)&=&-\g-\int_0^\infty e^{-zt}dt\\&&+\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{e^{-t}-e^{-(n+1)t}-e^{-(z+1)t}+e^{-(z+n+1)t}}{1-e^{-t}}dt\end{eqnarray*}第2項の積分を後の積分に放り込みます。\begin{eqnarray*}\psi(z)&=&-\g\\&&+\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{-e^{-zt}+e^{-(z+1)t}+e^{-t}-e^{-(n+1)t}-e^{-(z+1)t}+e^{-(z+n+1)t}}{1-e^{-t}}dt\\&=&-\g+\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{-e^{-zt}+e^{-t}-e^{-(n+1)t}+e^{-(z+n+1)t}}{1-e^{-t}}dt\end{eqnarray*}
オイラー定数の表示を使う
前回導出した式$$\g=\int_0^\infty\left(\frac{1}{1-e^{-t}}-\frac{1}{t}\right)e^{-t}dt$$を用います。\begin{eqnarray*}\psi(z)&=&\int_0^\infty\left(\frac{1}{t}-\frac{1}{1-e^{-t}}\right)e^{-t}dt\\&&+\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{-e^{-zt}+e^{-t}-e^{-(n+1)t}+e^{-(z+n+1)t}}{1-e^{-t}}dt\end{eqnarray*}前者の積分と後者の積分で $\dfrac{e^{-t}}{1-e^{-t}}$ が打ち消しあいます。また $e^{-zt}$ の項は $n$ と無関係なので左の積分に移動させます。\begin{eqnarray*}\psi(z)&=&\int_0^\infty\left(\frac{e^{-t}}{t}-\frac{e^{-zt}}{1-e^{-t}}\right)dt\\&&+\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{-e^{-(n+1)t}+e^{-(z+n+1)t}}{1-e^{-t}}dt\\&=&\int_0^\infty\left(\frac{e^{-t}}{t}-\frac{e^{-zt}}{1-e^{-t}}\right)dt\\&&-\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{1-e^{-zt}}{1-e^{-t}}e^{-(n+1)t}dt\end{eqnarray*}よってここまでで\begin{equation}\psi(z)=\int_0^\infty\left(\frac{e^{-t}}{t}-\frac{e^{-zt}}{1-e^{-t}}\right)dt-\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{1-e^{-zt}}{1-e^{-t}}e^{-(n+1)t}dt\tag{2}\end{equation}が成立することが分かりました。
極限の計算
(2)の $\lim$ をどうにかしましょう。その中身は\begin{multline}\left|\int_0^\infty\frac{1-e^{-zt}}{1-e^{-t}}e^{-(n+1)t}dt\right|\\\le\left|\int_0^1\frac{1-e^{-zt}}{1-e^{-t}}e^{-(n+1)t}dt\right|+\left|\int_1^\infty\frac{1-e^{-zt}}{1-e^{-t}}e^{-(n+1)t}dt\right|\end{multline}という不等式になります。
まず右辺第1項についてはロピタルの定理により$$\displaystyle\lim_{t\to0} \frac{1-e^{-zt}}{1-e^{-t}}=\displaystyle\lim_{t\to0} \frac{ze^{-zt}}{e^{-t}}=z$$よって $\dfrac{1-e^{-zt}}{1-e^{-t}}$ は $0\le t\le1$ で有界です。よって定数 $M$ が存在して$$\therefore\;\left|\int_0^1\frac{1-e^{-zt}}{1-e^{-t}}e^{-(n+1)t}dt\right|\le\left|\int_0^1Me^{-(n+1)t}dt\right|\xrightarrow[]{n\to\infty}0$$とできます。
次に右辺第2項については $t\ge1$ ですから\begin{eqnarray*}\left|\frac{1-e^{-zt}}{1-e^{-t}}\right|&\le&\frac{\left|1-e^{-zt}\right|}{1-e^{-1}}\le\frac{1+\left|e^{-zt}\right|}{1-e^{-1}}\\&=&\frac{1+\left|e^{-(\mathfrak{R}z)t}\right|}{1-e^{-1}}\le\frac{1+1}{1-e^{-1}}\end{eqnarray*}で有界です。よって定数 $M'$ が存在して$$\therefore\;\left|\int_1^\infty\frac{1-e^{-zt}}{1-e^{-t}}e^{-(n+1)t}dt\right|\le\left|\int_1^\infty M'e^{-(n+1)t}dt\right|\xrightarrow[]{n\to\infty}0$$
以上から(2)の $\lim$ は$$\displaystyle\lim_{n\to\infty}\int_0^\infty\frac{1-e^{-zt}}{1-e^{-t}}e^{-(n+1)t}dt=0$$であり、最終的な等式
\begin{equation}\psi(z)=\int_0^\infty\left(\frac{e^{-t}}{t}-\frac{e^{-zt}}{1-e^{-t}}\right)dt\tag{3}\end{equation}
を得ます。これが1つめの積分表示です。
(3)の被積分関数は2つの項からなりますが、これを分けて別々に積分すると $t=0$ のせいで発散してしまいます。そこで積分区間の下端を小さな正の数 $\epsilon$ としておきます。その上で積分を分けて後者のみ $t=\log(1+s)$ とおくと$$\psi(z)=\int_\epsilon^\infty\frac{e^{-t}}{t}dt-\int_{e^\epsilon-1}^\infty\frac{ds}{s(1+s)^z}$$右辺の1つめの積分区間を分けます。$$\int_\epsilon^\infty\frac{e^{-t}}{t}dt=\int_\epsilon^{e^\epsilon-1}\frac{e^{-t}}{t}dt+\int^\infty_{e^\epsilon-1}\frac{e^{-t}}{t}dt$$2つめの積分の $s$ を $t$ と書き換えます。$$\psi(z)=\int_\epsilon^{e^\epsilon-1}\frac{e^{-t}}{t}dt+\int_{e^\epsilon-1}^\infty\left(\frac{e^{-t}}{t}-\frac{1}{t(1+t)^z}\right)dt$$右辺第1項は$$\int_\epsilon^{e^\epsilon-1}\frac{e^{-t}}{t}dt\le \int_\epsilon^{e^\epsilon-1}\frac{dt}{t}=\log\frac{e^\epsilon-1}{\epsilon}\xrightarrow[]{\epsilon\to0}0$$
従って $\epsilon\to0$ とすることで次の公式を得ます。
\begin{equation}\psi(z)=\int_{0}^\infty\left(e^{-t}-\frac{1}{(1+t)^z}\right)\frac{dt}{t}\tag{4}\end{equation}
(3)で $e^{-t}=s$ と置換すると$$\psi(z)=\int_1^0\left(\frac{s}{-\log s}-\frac{s^z}{1-s}\right)\left(-\frac{ds}{s}\right)$$式を整理して $s$ を $t$ に書き換えると新たな積分表示を得ます。
\begin{equation}\psi(z)=\int_0^1\left(-\frac{1}{\log t}-\frac{t^{z-1}}{1-t}\right)dt\tag{5}\end{equation}
前回の記事でオイラー定数の積分表示を紹介しました。本記事ではディガンマ関数を扱ったので $\psi(1)=-\g$ によってオイラー定数 $\g$ の新たな積分表示を得ることが可能です。例えば(4)で $z=1$ とすると
\begin{equation}\g=\int_0^\infty\left(\frac{1}{1+t}-e^{-t}\right)\frac{dt}{t}\tag{6}\end{equation}
今回もやはり巧妙な技で数式を扱ったものの、初等的であり高校数学でも頑張れば理解できるレベルだったと思います。次回は少し重たいですが「ビネの第1公式」を導出します。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。


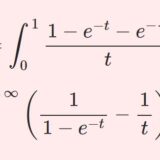

極限の計算での部分でロピタルの定理を使っていますが,
lim t->0{1-e^(-zt)}/{1-e^(-t)}=z
でしょうか?
ご指摘ありがとうございます。おっしゃる通りでした。訂正いたしました。またよろしくお願いします。