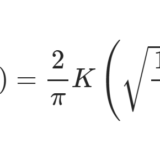前回はこちら:
前回の復讐です。
第1種ルジャンドル関数を次で定義する。$$P_\nu(z)=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+1}}dt\quad(\nu\in\CC\;,\, z\neq -1)$$ただし経路 $C$ は $1,z$ を時計回りに囲むが $-1$ は囲まない.
$\nu$ が非整数の場合、$t$ 平面には $1$ と $z$ を結ぶ切断、$-1$ と $-\infty$ を結ぶ切断を入れる.
前回はこの定義を使って $P_\nu(z)$ の値をいくつか計算しました。今回は導関数 $P_\nu'(z)$ の特殊値を計算しましょう。
定義1およびそれを微分したものは\begin{align}P_\nu(z)&=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+1}}dt\tag{0}\\P'_\nu(z) &=\frac{\nu+1}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+2}}dt\tag{1}\\ P''_\nu(z) &=\frac{(\nu+1)(\nu+2)}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+3}}dt\tag{2}\end{align}なお前回確認したように、導関数はルジャンドルの微分方程式を満たすので\begin{equation}(1-z^2)P_\nu''(z)-2zP_\nu'(z)+\nu(\nu+1)P_\nu(z)=0\tag{3}\end{equation}が成り立っています。
前回の方法にならって、これらの積分を計算してみましょう。$z=1$ の場合は\begin{align}P_\nu(1)&=\frac{1}{2\pi i}\oint_C\frac{(t+1)^\nu}{2^\nu(t-1)}dt\tag{4}\\P'_\nu(1) &=\frac{\nu+1}{2\pi i}\oint_C\frac{(t+1)^\nu}{2^\nu(t-1)^2}dt\tag{5}\\ P''_\nu(1) &=\frac{(\nu+1)(\nu+2)}{2\pi i}\oint_C\frac{(t+1)^\nu}{2^\nu(t-1)^3}dt\tag{6}\end{align}$C$ は $t=1$ を囲み、$t=-1$ を囲まないので、留数計算をします。(4)は1位の極、(5)は2位の極、(6)は3位の極となっていますから\begin{align}P_\nu(1)&=\frac{1}{2^\nu}\lim_{t\to 1}(t+1)^\nu\tag{7}\\P'_\nu(1) &=\frac{\nu+1}{2^\nu}\lim_{t\to 1}\frac{d}{dt}(t+1)^\nu\tag{8}\\ P''_\nu(1) &=\frac{(\nu+1)(\nu+2)}{2^{\nu+1}}\lim_{t\to1 }\frac{d^2}{dt^2}(t+1)^\nu\tag{9}\end{align}計算すると
\begin{align}P_\nu(1)&=1\tag{10}\\P'_\nu(1) &=\frac{\nu(\nu+1)}{2}\tag{11}\\ P''_\nu(1) &=\frac{(\nu-1)\nu(\nu+1)(\nu+2)}{8}\tag{12}\end{align}
$\nu$ が整数のとき(ルジャンドル多項式)で試すと、定理2は確かに合っています。
ついでに $\nu=-1/2$ でも確認してみました。定理2によれば\begin{equation}P_{-\frac{1}{2}}(1)=-\frac{1}{8}\tag{13}\end{equation}です。これは前回に導出した$$P_{-\frac{1}{2}}(x)=\frac{2}{\pi} K\left(\sqrt{\frac{1-x}{2}}\right)\;,\quad -1<x\le 1$$からも導けるはずです。これを微分すると$$P'_{-\frac{1}{2}}(x)=-\frac{1}{2\pi k} \frac{dK(k)}{dk}\;,\quad k=\sqrt{\frac{1-x}{2}}$$ここで完全楕円積分の級数表示$$K(k)=\frac{\pi}{2}\sum_{n=0}^\infty \left(\frac{(2n-1)!!}{(2n)!!}\right)^2k^{2n}$$を微分した式$$\frac{dK(k)}{dk}=\frac{\pi}{2}\sum_{n=0}^\infty \frac{(2n-1)!!^2}{(2n)!!(2n+2)!!}k^{2n}$$を適用して$$P'_{-\frac{1}{2}}(x)=-\frac{1}{4}\sum_{n=0}^\infty \frac{(2n-1)!!^2}{(2n)!!(2n+2)!!}\left(\frac{1-x}{2}\right)^n$$これに $x=1$ を代入すると(13)に一致します。
今回は短いですがここまで。次回は:
 ルジャンドル関数の基礎4~漸化式
ルジャンドル関数の基礎4~漸化式
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。