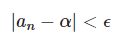単振り子の周期は厳密には振幅に依存する。本記事ではこの事実を運動方程式を解くことで証明する。しかし解析的に積分が実行できないため、項別積分によって無限級数で周期を表現する。その結果、式を見ると周期は確かに振幅（最大角）に依存し、振幅が十分小さければ高校物理での周期の式が現れることを解説する。
長さ $l$ の単振り子を考えます。高等学校では、振れ幅が十分に小さいときはおもりの運動は単振動となり、その周期は $2\pi\sqrt{\displaystyle\frac{l}{g}}$ です。つまり周期は $l$ のみにより、振れ幅は関係がないことになります。これを振り子の等時性といいます。
しかしこれは振れ幅が十分に小さいとしたときの近似の結果です。厳密にはどうなのでしょうか？
ニュートンの運動方程式から単振り子の周期を計算し，等時性が厳密に成り立つか検証せよ．
極座標成分でベクトルを扱います．詳細は
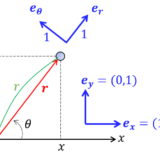【H6】ベクトルの極座標成分
を参照ください．
鉛直下方向を$x$軸として $xy$ 平面内で運動する単振り子を考えます。糸が $x$ 軸から $\theta$ の角度をなしているときのおもりの座標は $\boldsymbol{r}=l(\cos\theta , \sin\theta)=l\bm{e}_r$ です。これを2階微分すると加速度となります。\begin{eqnarray*}\ddot{\boldsymbol{r}}&=&l\frac{d}{dt}(-\dot{\theta}\sin\theta, \dot{\theta}\cos\theta)\\&=& l(-\ddot{\theta}\sin\theta-\dot{\theta}^2\cos\theta , \ddot{\theta}\cos\theta-\dot{\theta}^2\sin\theta)\\&=&-l\dot{\t}^2\bm{e}_r+l\ddot{\t}\bm{e}_\t\end{eqnarray*}おもりにかかる力は張力 $S$ として$$\bm{F}=(mg\cos\t-S)\bm{e}_r-mg\sin\t\bm{e}_\t$$よって運動方程式 $\bm{F}=m\ddot{\bm{r}}$ より$$(mg\cos\t-S)\bm{e}_r-mg\sin\t\bm{e}_\t=-ml\dot{\t}^2\bm{e}_r+ml\ddot{\t}\bm{e}_\t$$動径成分からは張力の大きさが求められそうですが本題とは無関係です．角度方向の式は$$l\ddot{\theta} =-g\sin\theta$$$\displaystyle\frac{g}{l}=\omega^2$とおくと$$\ddot{\theta}=-\omega^2 \sin\theta$$これが今回解くべき方程式となります。
$\dot{\theta}$ をかけると$$\dot{\theta}\ddot{\theta}=-\omega^2 \dot{\theta}\sin\theta$$となるので$$\frac{d}{dt}\left( \frac{1}{2}\dot{\theta}^2\right)=\frac{d}{dt}\left(\omega^2\cos\theta \right)$$
時刻 $t=0$ において $\theta$ は最大値 $\theta_0$ をとり、角速度 $\dot{\theta}(0)=0$ とします。$t$ で積分をして$$\dot{\theta}^2=2\omega^2(\cos\theta-\cos\theta_0)=4\omega^2\left( \sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}\right)$$ここで $\dot{\theta}=\displaystyle\frac{d\theta}{dt}$ なので$$\therefore dt=\frac{d\theta}{2\omega\sqrt{\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}}}$$おもりの運動の対称性から周期の1/4すなわち $\theta :0\rightarrow\theta_0$ の範囲で積分します。$$\frac{T}{4}=\frac{1}{2\omega}\int_0^{\theta_0}\frac{d\theta}{\sqrt{\sin^2\frac{\theta_0}{2}-\sin^2\frac{\theta}{2}}}$$これで周期 $T$ を積分であらわすことができました。
ここで変数変換を施します。$$\sin\displaystyle\frac{\theta}{2}=\sin\frac{\theta_0}{2}\sin\phi$$さらに $\displaystyle\sin\frac{\theta_0}{2}=k$ とすれば$$T=\frac{4}{\omega}\int^\frac{\pi}{2}_0\frac{d\phi}{\sqrt{1-k^2\sin^2\phi}}$$ これは第一種完全楕円積分とよばれ、まともに積分できません（楕円積分についてはこちら）。なので無限級数に展開します。
分数関数の展開式$$\frac{1}{\sqrt{1-x}}=\sum^\infty_{n=0}\frac{(2n-1)!!}{(2n)!!}x^n$$に $x=k^2\sin^2\phi$ を代入することにより\begin{eqnarray*}T&=&\frac{4}{\omega}\sum^\infty_{n=0}\frac{(2n-1)!!}{(2n)!!}k^{2n}\int^\frac{\pi}{2}_0\sin^{2n}\phi d\phi\\&=&\frac{4}{\omega}\sum^\infty_{n=0}\frac{(2n-1)!!}{(2n)!!}k^{2n}\cdot \frac{(2n-1)!!}{(2n)!!}\cdot\frac{\pi}{2}\end{eqnarray*}以上より $\omega=\sqrt{\displaystyle\frac{g}{l}}$ と戻して$$T=2\pi\sqrt{\frac{l}{g}}\sum^\infty_{n=0}\left( \frac{(2n-1)!!}{(2n)!!}\right)^2\sin^{2n}\frac{\theta_0}{2}$$
見れば分かるように周期には $\theta_0$ が含まれており、振れ幅に依存していることが分かります。最初の2,3項だけ書き下してみれば分かりますが $\theta_0$が小さいときは第1項($n=0$の項)以外は無視でき、振れ幅に依存しないと考えてもよいことが確認できます。$$T\approx 2\pi\sqrt{\frac{l}{g}}$$
単振り子の周期 $T$ は厳密には$$T= 2\pi\sqrt{\frac{l}{g}}\sum^\infty_{n=0}\left( \frac{(2n-1)!!}{(2n)!!}\right)^2\sin^{2n}\frac{\theta_0}{2}$$と表される。これは角度の最大値 $\theta_0$ に依存しているため、周期は振幅によって変化することになる。よって等時性は破れている。
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
