nが3以上のときは適切な置換を用いることでガンマ関数に帰着することが証明できる。オマケとして関数列の一様連続性および一様有界性から極限の取り換えが可能であることも説明する。
$e^{-x}$ の積分は高等学校で学習し、$e^{-x^2}$ の積分も「ガウス積分」としてよく知られています。では $e^{-x^3}\;,\;e^{-x^4}\cdots$ の場合はどうでしょうか。
$$I_n=\int_0^\infty e^{-x^n}dx\;\;\; (n\in\mathbb{N})$$はいかなる値か．
結論から言いますと $n=1,2$ 以外では数値を求められません。$$I_1=1$$$$I_2=\frac{\sqrt{\pi}}{2}$$$$I_3=??$$しかし $n\ge 3$ ではガンマ関数に帰着させることができます。
ガンマ関数は次のように定義されます。
$$\Gamma (s)=\int_0^\infty e^{-x}x^{s-1}dx\;\;\; (\textrm{Re}\; s>0)$$
これが階乗を実数全体に拡張したものになっているのは有名です。$$\Gamma(s+1)=s\Gamma(s)$$
$I_n\; (n\ge2)$ において $x^n=y$ とおくと$$I_n=\frac{1}{n}\int_0^\infty e^{-y}y^{\frac{1}{n}-1}dy$$よってガンマ関数の定義から明らかなように$$I_n=\frac{1}{n}\Gamma\left(\frac{1}{n}\right)=\Gamma\left(\frac{n+1}{n}\right)$$この $I_n$ は $n=1$ でも成立していますので、すべての自然数 $n$ に対して積分値を調べることができました。
$$\int_0^\infty e^{-x^n}dx = \Gamma\left(\frac{n+1}{n}\right)$$
数値を求めたわけではありませんがガンマ関数にすることで多少分かりやすくなっています。例えば $n$ が大きいと $1$ に近づいていくんだな、とか。ちなみに $I_{100}=\Gamma(101/100)\approx 0.994$ となります。
なお被積分関数列 $f_n(x)=e^{-x^n} $ は区間 $[0,\infty)$ において$$f(x)=\begin{cases} 1 & (0\le x<1) \\ 1/e & (x=1)\\ 0 & (x>1)\end{cases} $$へ収束します。$x=1$ 付近のせいで関数列は一様収束しませんが、
・積分してから極限を取った場合$$\displaystyle\lim_{n\to\infty}I_n=1$$
・極限をとって $(f_n\to f)$ から積分した場合$$\int_0^\infty f(x)=1$$
となり、操作を取り換えても値が変わらない例です。取り換え可能であることは、各 $n$ に対して関数 $f_n(x)$ が $[0,\infty)$ において一様有界かつ一様連続であることから示すこともできます。
一様有界であることは明らかです。一様連続であることは以下のように示せます。
$n=1$ では簡単に示せるので $n\ge 2$ とし、各 $n$ について $f_n(x)=e^{-x^n} $ が微分可能であることを認めれば$$f_n'(x)=-nx^{n-1}e^{-x^n} $$これをさらに微分して増減を調べてみると、 $x\ge 0$ において$$|f_n'(x)|\le n\left(\frac{n-1}{en}\right)^{\frac{n-1}{n}}< n$$と押さえることができます。さて、任意の $\epsilon >0$ に対して $\delta =\epsilon /n$ ととると平均値の定理により$$|f_n(x)-f_n(y)|\le n\left(\frac{n-1}{en}\right)^{\frac{n-1}{n}}|x-y|<n|x-y|<n\delta =\epsilon$$となって、一様連続です。一様連続かつ一様有界ですので、極限の交換ができます。
関連記事：
【複素解析】cos(x^n),sin(x^n) の定積分（フレネル積分を一般化）
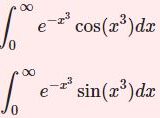$\int e^{-x^n}\sin(x^n)dx$ の積分（ガンマ関数）
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
