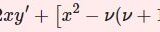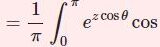一般相対論であらわれるスカラー曲率を計算する.相対論とからめた内容ではなく,テンソル計算の練習である.
球の半径を $a$ として極座標をとる
共変・反変ともに
この場合、実質6成分
成分が多いが、非ゼロ成分だけ考えればよい
リーマン曲率テンソルの内部で積をとったもの
リッチテンソルと計量テンソルの積である
微小な線分 $ds$ は計量テンソル $g$ を用いて$$ds^2=g_{\mu\nu} dx^\mu dx^\nu$$であり,反変 $g^{\mu\nu}$ はその逆行列として表現できる.またクリストッフェル記号 $\Gamma$ は$$\Gamma^\mu_{\alpha\beta}=\frac{1}{2}g^{\mu\lambda}\left(\frac{\partial g_{\beta\lambda}}{\partial x^{\alpha}}+ \frac{\partial g_{\lambda\alpha}}{\partial x^{\beta}}-\frac{\partial g_{\alpha\beta}}{\partial x^{\lambda}}\right)$$であるが,本記事では空間成分のみ扱うため,添え字はギリシャ文字ではなくふつうのアルファベットを用いる.
クリストッフェル記号からリーマン曲率テンソルが求まる.$$R^i_{jkl}\equiv\partial_k\Gamma^i_{jl}-\partial_l\Gamma^i_{jk}+\Gamma^m_{jl}\Gamma^i_{mk}-\Gamma^m_{jk}\Gamma^i_{ml}$$ただし $\partial_i$ は $x^i$ による偏微分を表す.
さらにこれからリッチテンソルが求まる.$$R_{ij}\equiv R^k_{ikj}$$最後にリッチスカラーは$$R\equiv g^{ij}R_{ij}$$以上のような流れである.
今回は二次元球面上の任意の点におけるスカラー曲率を求める.球の半径を $a$ とする.直交座標からの座標変換は$$\begin{cases}x&=&a\sin\theta\cos\phi\\y&=&a\sin\theta\sin\phi\\z&=&a\cos\theta\end{cases}$$それぞれ全微分は$$\begin{cases}dx&=&a\cos\theta\cos\phi d\theta-a\sin\theta\sin\phi d\phi\\ dy &=& a\cos\theta\sin\phi d\theta+a\sin\theta\cos\phi d\phi\\ dz&=& -a\sin\theta d\theta\end{cases}$$微小距離 $ds^2=dx^2+dy^2+dz^2$ に代入すると$$ds^2=a^2d\theta^2+a^2\sin^2\theta d\phi^2$$を得る.よって計量テンソルの非ゼロ成分は$$g_{\theta\theta}=a^2\;,\;g_{\phi\phi}=a^2\sin^2\theta$$反変テンソルはその逆行列を考えるとよいので,非ゼロ成分は$$g^{\theta\theta}=\frac{1}{a^2}\;,\;g^{\phi\phi}=\frac{1}{a^2\sin^2\theta}$$となる.
クリストッフェル記号 $\Gamma^\mu_{\alpha\beta}$ は添え字それぞれ $\t$ , $\phi$ をとるので8成分に見えるが,下付きの2つの添え字を入れ替えても変わらないことから実質$6$成分である.実際の計算は先ほどの計量テンソルを用いて$$\Gamma^i_{jk}=\frac{1}{2}g^{im}\left(\partial_j g_{km}+ \partial_k g_{mj}-\partial_m g_{jk}\right)$$となるので,これをがんばって計算すると非ゼロ成分は$$\Gamma^\theta_{\phi\phi}=-\sin\theta\cos\theta\;,\; \Gamma^\phi_{\phi\theta}=\Gamma^\phi_{\theta\phi}=\cot\theta$$となる.
リーマン曲率テンソルは$$R^i_{jkl}\equiv\partial_k\Gamma^i_{jl}-\partial_l\Gamma^i_{jk}+\Gamma^m_{jl}\Gamma^i_{mk}-\Gamma^m_{jk}\Gamma^i_{ml}$$で与えられる.クリストッフェル記号の微分が出てきて大変そうである.しかし $\Gamma$ の微分の非ゼロ成分は$$\partial_\theta\Gamma^\theta_{\phi\phi}=2\sin^2\theta-1$$$$\partial_\theta\Gamma^\phi_{\phi\theta}=\partial_\theta\Gamma^\phi_{\theta\phi}=-\frac{1}{\sin^2\theta}$$のみである.なんとか頑張って計算すると非ゼロ成分は$$\begin{cases}R^\theta_{\phi\theta\phi} &=& \sin^2\theta\\R^\theta_{\phi\phi\theta} &=& -\sin^2\theta\\R^\phi_{\theta\theta\phi} &=& -1\\R^\phi_{\theta\phi\theta}&=&1\end{cases}$$と求まる.
リッチテンソルはリーマン曲率テンソルの内部で積をとったものである.$$R_{ij}\equiv R^k_{ikj}$$上の添え字と下の真ん中の添え字が同じもので和を取るため$$\begin{cases}R_{\theta\theta}=R^\theta_{\theta\theta\theta}+R^\phi_{\theta\phi\theta}=1\\R_{\phi\phi}=R^\theta_{\phi\theta\phi}+R^\phi_{\phi\phi\phi}=\sin^2\theta\\R_{\theta\phi}=R^\theta_{\theta\theta\phi}+R^\phi_{\theta\phi\phi}=0\\R_{\phi\theta}=R^\theta_{\phi\theta\theta}+R^\phi_{\phi\phi\theta}=0\end{cases}$$
リッチテンソルと計量テンソルの積をとることでリッチスカラーが求まる.\begin{eqnarray*}R&\equiv& g^{ij}R_{ij}\\&=& g^{\theta\theta}R_{\theta\theta}+g^{\phi\phi}R_{\phi\phi}+0+0\\&=&\frac{1}{a^2}+\frac{1}{a^2\sin^2\theta}\sin^2\theta\\&=&\frac{2}{a^2}\end{eqnarray*}
ガウス曲率 $1/a^2$ の2倍になっていることが分かる.
これで座標設定からリッチスカラー導出までの一連の流れが体験できた.
アインシュタインテンソルは$$G_{\mu\nu}\equiv R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R$$と定義される.これを計算すると$$G_{\theta\theta}=G_{\phi\phi}=G_{\theta\phi}=G_{\phi\theta}=0$$すなわちアインシュタインテンソルは全成分ゼロとなる.
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。