\begin{equation}\frac{d^2x^\mu}{ds^2}+\G^\mu_{\alpha\beta}\frac{dx^\alpha}{ds}\frac{dx^\beta}{ds}=0\tag{1}\end{equation}
一般相対論や微分幾何学で現れる測地線方程式です.
測地線とは曲がった空間(時空)における「直線」のことです.実際にこれを計算する例題が少ないので簡単なものを取り上げていきます.なお添え字の意味とか簡単なテンソル計算の方法等,一般相対論の初歩的な知識を前提としています.扱う例題は「2次元平面(直交座標・極座標)」「2次元球面」「弱い重力場の時空」.
もくじ
微小な線分 $ds$ は計量テンソル $g$ を用いて
\begin{equation}ds^2=g_{\mu\nu} dx^\mu dx^\nu\tag{2}\end{equation}
計量テンソルは添え字を逆転させても同じ値です.$$g_{\mu\nu}=g_{\nu\mu}$$またクリストッフェルの記号 $\Gamma^\mu_{\alpha\beta}$ は
\begin{equation}\Gamma^\mu_{\alpha\beta}=\frac{1}{2}g^{\mu\lambda}\left(\frac{\partial g_{\beta\lambda}}{\partial x^{\alpha}}+ \frac{\partial g_{\lambda\alpha}}{\partial x^{\beta}}-\frac{\partial g_{\alpha\beta}}{\partial x^{\lambda}}\right)\tag{3}\end{equation}
です.測地線方程式(1)を具体的に書き表すにはこのクリストッフェル記号を計算しておく必要があります.これがなかなか面倒くさいです.ともかく例題をやっていきましょう.
まずは2次元平面でやってみましょう.2次元平面の座標系といえば $xy$ 直交座標系です.単純すぎて練習にならないかもしれませんが.でもいきなり時間+3次元では大変ですからちょうどいいと思います.これができたらあえて極座標でやってみます.
$xy$ 直交座標においては微小距離$$ds^2=dx^2+dy^2$$ですから,(2)と見比べると$$g_{xx}=g_{yy}=1\;,\;g_{xy}=g_{yx}=0$$次のように行列で表現するのも簡潔でいいでしょう.$$(g)_{ij}=\begin{pmatrix}1 & 0\\ 0 & 1\end{pmatrix}$$
計量テンソルの成分がすべて定数であることからクリストッフェル記号(3)は全成分において$0$です.$$ \Gamma^m_{ab}=0\quad(m,a,b=1,2) $$よって測地線方程式は$$\begin{cases}\displaystyle\frac{d^2x}{ds^2}&=&0\\\displaystyle\frac{d^2y}{ds^2}&=&0\end{cases}$$また $ds^2=dx^2+dy^2$ を変形して$$\left(\frac{dx}{ds}\right)^2+\left(\frac{dy}{ds}\right)^2=1$$これで必要な微分方程式が揃いました.
まず $\displaystyle\frac{d^2x}{ds^2}=\displaystyle\frac{d^2y}{ds^2}=0$ から $$\frac{dx}{ds}=const.\quad ,\quad\frac{dy}{ds}=const.$$ですが $\left(\displaystyle\frac{dx}{ds}\right)^2+\left(\displaystyle\frac{dy}{ds}\right)^2=1$ から定数の具体的な形を考慮すると$$\frac{dx}{ds}=\cos\phi\quad ,\quad\frac{dy}{ds}=\sin\phi\quad (\phi :\mathrm{const.})$$とできます.それぞれ積分すると$$x=s\cos\phi+x_0\quad,\quad y=s\sin\phi+y_0$$媒介変数となっている $s$ を消去して$$y-y_0=\tan\phi\cdot(x-x_0)$$これは直線をあらわします.
つまり2次元平面の測地線は直線です.
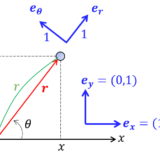
あまりに簡単すぎたので極座標表示でもやってみます.測地線が直線であるという結果はこちらでも導出できるはずです.まずは微小距離の式\begin{equation}ds^2=dr^2+r^2d\theta^2\tag{4}\end{equation}より計量テンソルの4成分は$$g_{rr}=1\;,\;g_{\theta\theta}=r^2\;,\;g_{r\t}=g_{\t r}=0$$ 反変テンソルはその逆行列を考えるとよいので$$g^{rr}=1\;,\;g^{\theta\theta}=\frac{1}{r^2}\;,\;g^{r\t}=g^{\t r}=0$$
クリストッフェル記号 $\Gamma^\mu_{\alpha\beta}$ は下付きの2つの添え字を入れ替えても変わらないことから実質$6$成分であり,$\Gamma^r_{rr}$ , $\Gamma^r_{r\theta}$ , $\Gamma^r_{\theta\theta}$ , $\Gamma^\theta_{rr}$ , $\Gamma^\theta_{r\theta}$ , $\Gamma^\theta_{\theta\theta}$ を(3)により計算すればよいです.がんばって計算すると非ゼロ成分は$$\Gamma^r_{\theta\theta}=-r\quad,\quad \Gamma^\theta_{r\theta}=\frac{1}{r}$$これにより測地線方程式は\begin{equation}\begin{cases}\displaystyle\frac{d^2r}{ds^2}-r\left(\displaystyle\frac{d\theta}{ds}\right)^2=0\\\displaystyle\frac{d^2\theta}{ds^2}+\displaystyle\frac{2}{r}\displaystyle\frac{d\theta}{ds}\displaystyle\frac{dr}{ds}=0\end{cases}\tag{5}\end{equation}であり,微小距離の式(4)を変形した\begin{equation}\left(\frac{dr}{ds}\right)^2+r^2\left(\frac{d\theta}{ds}\right)^2=1\tag{6}\end{equation}も併せて3つの微分方程式ができました.
それでは解いていきましょう.まず測地線方程式(5)の下側の式を変形します.\begin{eqnarray*}&&\frac{d^2\theta}{ds^2}+\frac{2}{r}\frac{d\theta}{ds}\frac{dr}{ds}=0\\\Leftrightarrow&& r^2\frac{d^2\theta}{ds^2}+2r\frac{d\theta}{ds}\frac{dr}{ds}=0\\\Leftrightarrow&& \frac{d}{ds}\left(r^2\frac{d\theta}{ds}\right)=0\\\Leftrightarrow&& r^2\frac{d\theta}{ds}=A\quad(\mathrm{const.})\\\Leftrightarrow&& \frac{d\theta}{ds}=\frac{A}{r^2}\end{eqnarray*}
これにより(5)の上側の測地線方程式は\begin{eqnarray*}&&\frac{d^2r}{ds^2}-r\left(\frac{d\theta}{ds}\right)^2=0\\\Leftrightarrow&& \frac{d^2r}{ds^2}=r\left(\frac{A}{r^2}\right)^2\\\Leftrightarrow&& \frac{d^2r}{ds^2}=\frac{A^2}{r^3}\end{eqnarray*}ですがこれを解くのは困難なので保留です。
さらに微小距離の式(6)から\begin{eqnarray*}&&\left(\frac{dr}{ds}\right)^2=1-r^2\left(\frac{d\theta}{ds}\right)^2\\\Leftrightarrow&& \left(\frac{dr}{ds}\right)^2=1-r^2\frac{A^2}{r^4}\\\therefore &&\frac{dr}{ds}=\sqrt{1-\frac{A^2}{r^2}}\end{eqnarray*}これを先ほど保留した方程式に代入すると成立します.
以上から$$\frac{d\theta}{ds}=\frac{A}{r^2}\;,\;\frac{dr}{ds}=\sqrt{1-\frac{A^2}{r^2}}$$を得ました.従って\begin{eqnarray*}\frac{d\theta}{dr}&=&\frac{d\theta/ds}{dr/ds}\\ &=& \frac{A/r^2}{\sqrt{1-A^2/r^2}}\\\therefore&& \theta = \mathrm{arcsec} \frac{r}{A}+\theta_0\\\Leftrightarrow&& \frac{A}{r}=\cos(\theta-\theta_0)\\\Leftrightarrow&& A=r\cos\theta\cos\theta_0+r\sin\theta\sin\theta_0\\\Leftrightarrow&& A=\cos\theta_0x+\sin\theta_0y \end{eqnarray*}これは直線を表します。
測地線方程式の2つの具体的な計算を見てきました.平面なので何か面白い結論が出たわけではありませんし,その割に計算も邪魔くさいのでわりに合わない感じですね.でもこの方程式が,ちゃんと私たちの知っている世界で成り立っていることを確かめるのは大切だと思います.
また、そもそも測地線方程式は $\displaystyle\int ds$ の変分原理によって導出されますのでこの積分の変分をとることで同じ結果を得ることができます.ぜひ確かめてみてください.
次は球面の測地線方程式をやってみます.球面上の測地線が大円であることは予想できますが,実際そうなるでしょうか?重要な式を再掲しておきます.
\begin{equation}\frac{d^2x^\mu}{ds^2}+\G^\mu_{\alpha\beta}\frac{dx^\alpha}{ds}\frac{dx^\beta}{ds}=0\tag{1}\end{equation}\begin{equation}ds^2=g_{\mu\nu} dx^\mu dx^\nu\tag{2}\end{equation}\begin{equation}\Gamma^\mu_{\alpha\beta}=\frac{1}{2}g^{\mu\lambda}\left(\frac{\partial g_{\beta\lambda}}{\partial x^{\alpha}}+ \frac{\partial g_{\lambda\alpha}}{\partial x^{\beta}}-\frac{\partial g_{\alpha\beta}}{\partial x^{\lambda}}\right)\tag{3}\end{equation}
測地線方程式を導く
球の半径 $R$ とします.直交座標からの座標変換は$$x=R\sin\theta\cos\phi\;,\;y=R\sin\theta\sin\phi\;,\;z=R\cos\theta$$ですので微小距離の式は\begin{equation}ds^2=R^2d\theta^2+R^2\sin^2\theta d\phi^2\tag{7}\end{equation}計量テンソルの非ゼロ成分は$$g_{\theta\theta}=R^2\;,\;g_{\phi\phi}=R^2\sin^2\theta$$これより反変テンソルを計算すると非ゼロ成分は$$g^{\theta\theta}=\frac{1}{R^2}\;,\;g^{\phi\phi}=\frac{1}{R^2\sin^2\theta}$$クリストッフェル記号 $\Gamma^\mu_{\alpha\beta}$ は下付きの2つの添え字を入れ替えても変わらないことから実質$6$成分です.がんばって計算すると非ゼロ成分は$$\Gamma^\theta_{\phi\phi}=-\sin\theta\cos\theta\;,\; \Gamma^\phi_{\phi\theta}=\Gamma^\phi_{\theta\phi}=\cot\theta$$これにより測地線方程式(1)は\begin{equation}\begin{cases}\displaystyle\frac{d^2\theta}{ds^2}-\sin\theta\cos\theta\left(\displaystyle\frac{d\phi}{ds}\right)^2=0\\\displaystyle\frac{d^2\phi}{ds^2}+2\cot\theta\displaystyle\frac{d\theta}{ds}\displaystyle\frac{d\phi}{ds}=0\end{cases}\tag{8}\end{equation}となります.
測地線を求める
まず(8)の下側を変形します.\begin{eqnarray*}&&\frac{d^2\phi}{ds^2}+2\cot\theta\frac{d\theta}{ds}\frac{d\phi}{ds}=0\\\Leftrightarrow&&\sin^2\theta\frac{d^2\phi}{ds^2}+2\sin\theta\cos\theta\frac{d\theta}{ds}\frac{d\phi}{ds}=0\\\Leftrightarrow&&\frac{d}{ds}\left(\sin^2\theta\frac{d\phi}{ds}\right)=0\end{eqnarray*}よって $\sin^2\theta\displaystyle\frac{d\phi}{ds}$ は定数になることが分かりますが,式(7)から$$1=R^2\left(\frac{d\theta}{ds}\right)^2+R^2\sin^2\theta\left(\frac{d\phi}{ds}\right)^2$$より $-1\le R\sin\theta\displaystyle\frac{d\phi}{ds}\le 1$ すなわち$$-\frac{1}{R}\le\sin^2\theta\frac{d\phi}{ds}\le\frac{1}{R}$$を満たしますので,定数 $a$ を用いて\begin{equation}\sin^2\theta\frac{d\phi}{ds}=\frac{\sin a}{R}\tag{9}\end{equation}と書けます.
次に(7)を変形します.$\theta$ と$\phi$ の媒介変数 $s$ を消しましょう.\begin{eqnarray*}&&ds^2=R^2d\theta^2+R^2\sin^2\theta d\phi^2\\\Leftrightarrow&&\left(\frac{ds}{d\phi}\right)^2=R^2\left(\frac{d\theta}{d\phi}\right)^2+R^2\sin^2\theta\\\Leftrightarrow&&\frac{R^2\sin^4\theta}{\sin^2a}=R^2\left(\frac{d\theta}{d\phi}\right)^2+R^2\sin^2\theta\;(\because(9))\\\Leftrightarrow&&\left(\frac{d\theta}{d\phi}\right)^2=\frac{\sin^4\theta}{\sin^2a}-\sin^2\theta\end{eqnarray*}$u\equiv\cot\theta$ とおくと,$d\theta=-\frac{1}{1+u^2}du$ なので$$\left(\frac{du}{d\phi}\right)^2=\cot^2a-u^2$$ $$\therefore\quad d\phi=\frac{du}{\sqrt{\cot^2a-u^2}}$$ここで右辺の符号は $-$ でも構いません.積分を実行して\begin{eqnarray*}&&\phi-\phi_0=\arcsin(u\tan a)\\\Leftrightarrow&&\phi-\phi_0=\arcsin(\tan a\cot\theta)\\\Leftrightarrow&&\sin(\phi-\phi_0)=\tan a\cot\theta\\\Leftrightarrow&&R\cos a\sin\theta\sin(\phi-\phi_0)-R\sin a\cos\theta=0\\\Leftrightarrow&&R\cos a\sin\theta(\sin\phi\cos\phi_0-\cos\phi\sin\phi_0)-R\sin a\cos\theta=0\\\Leftrightarrow&&-\cos a\sin\phi_0\cdot x+\cos a\cos\phi_0\cdot y-\sin a\cdot z=0\end{eqnarray*}$x,y,z$ の係数は定数なのでこれは $Ax+By+Cz=0$ の形であり,原点を通る平面を表します.その平面と球面が交わってできるのは大円です.よって測地線は大円です。
いよいよ時空でやってみましょう.重要な式を再掲します.
\begin{equation}\frac{d^2x^\mu}{ds^2}+\G^\mu_{\alpha\beta}\frac{dx^\alpha}{ds}\frac{dx^\beta}{ds}=0\tag{1}\end{equation}\begin{equation}ds^2=g_{\mu\nu} dx^\mu dx^\nu\tag{2}\end{equation}\begin{equation}\Gamma^\mu_{\alpha\beta}=\frac{1}{2}g^{\mu\lambda}\left(\frac{\partial g_{\beta\lambda}}{\partial x^{\alpha}}+ \frac{\partial g_{\lambda\alpha}}{\partial x^{\beta}}-\frac{\partial g_{\alpha\beta}}{\partial x^{\lambda}}\right)\tag{3}\end{equation}
また $A$ という量を $x^\mu$ で微分する場合,以下の記号を定義します.$$A,_\mu\equiv \frac{\partial A}{\partial x^\mu}$$
弱い重力場と計量テンソル
座標系 $x^0=ct$ , $x^1=x$ , $x^2=y$ , $x^3=z$ ととります.まず重力がまったくない平坦な時空は,特殊相対論でお馴染みのミンコフスキー計量 $\eta_{\mu\nu}$ で表されます.行列表示すると$$(\eta_{\mu\nu})=(\eta^{\mu\nu})=\left(\begin{matrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{matrix}\right)$$
弱い重力場を仮定すると計量 $g$ は $\eta$ から少しだけずれていると考えて$$g_{\mu\nu}=\eta_{\mu\nu}+h_{\mu\nu}\quad(|h_{\mu\nu}|\ll |\eta_{\mu\nu}|)$$$$g^{\mu\nu}=\eta^{\mu\nu}+h^{\mu\nu}\quad(|h^{\mu\nu}|\ll |\eta^{\mu\nu}|)$$とおくことにします.この重力場は時間によらない定常な場だとすると $x^0$ での偏微分がゼロになるので$$g_{\mu\nu},_0=0\Rightarrow h_{\mu\nu},_0=0$$ただし $\eta_{\mu\nu}$ が定数であることを用いました.
ここで微小距離の式を $0$ 成分と空間成分で分けて記述すると$$ds^2=g_{00}(dx^0)^2+2g_{0i}dx^0dx^i+g_{ij}dx^idx^j$$定常な重力場を考えるなら $x^0$ を $-x^0$ としても $ds^2$ は変化しませんので$$g_{0i}=0$$と導き出せます.
クリストッフェル記号
\begin{eqnarray*}\Gamma^\mu_{\alpha\beta}&=&\frac{1}{2}g^{\mu\lambda}(g_{\lambda\alpha},_\beta+g_{\lambda\beta},_\alpha-g_{\alpha\beta},_\lambda)\\&=& \frac{1}{2}(\eta^{\mu\lambda}+h^{\mu\lambda})(h_{\lambda\alpha},_\beta+h_{\lambda\beta},_\alpha-h_{\alpha\beta},_\lambda)\\&\approx& \frac{1}{2}\eta^{\mu\lambda}(h_{\lambda\alpha},_\beta+h_{\lambda\beta},_\alpha-h_{\alpha\beta},_\lambda)\end{eqnarray*}
下付き添え字が $00$ の成分を考えます.\begin{eqnarray*}\Gamma^\mu_{00}&\approx& \frac{1}{2}\eta^{\mu\lambda}(h_{\lambda 0},_0+h_{\lambda 0},_0-h_{00},_\lambda)\\&=&-\frac{1}{2}\eta^{\mu\lambda}h_{00},_\lambda\end{eqnarray*}$$\therefore\; \Gamma^0_{00}=0\;,\;\Gamma^i_{00}=\frac{1}{2}h_{00},_i$$
次に\begin{eqnarray*}\Gamma^i_{j0}&=&\frac{1}{2}g^{i\lambda}(g_{j\lambda },_0+g_{0\lambda},_j-g_{j0},_\lambda)\\&=& \frac{1}{2}g^{i\lambda}(g_{0\lambda},_j-g_{j0},_\lambda)\\&=& \frac{1}{2}g^{i0}(g_{00},_j-g_{j0},_0)+\frac{1}{2}g^{im}(g_{0m},_j-g_{j0},_m)\\&=& 0\end{eqnarray*}
空間成分の測地線方程式
以上から $x^i$ に関する測地線方程式は$$\frac{d^2x^i}{ds^2}+\Gamma^i_{\alpha\beta}\frac{dx^\alpha}{ds}\frac{dx^\beta}{ds}=0$$これまでの結果を用いて左辺を変形すると\begin{eqnarray*}&&\frac{d^2x^i}{ds^2}+\Gamma^i_{00}\left(\frac{dx^0}{ds}\right)^2+2\Gamma^i_{j0}\frac{dx^j}{ds}\frac{dx^0}{ds}+\Gamma^i_{jk}\frac{dx^j}{ds}\frac{dx^k}{ds}\\&=& \frac{d^2x^i}{ds^2}+\frac{1}{2}h_{00},_i\left(\frac{dx^0}{ds}\right)^2+\Gamma^i_{jk}\frac{dx^j}{ds}\frac{dx^k}{ds}\end{eqnarray*}\begin{equation}\therefore\;\frac{d^2x^i}{ds^2}+\frac{1}{2}h_{00},_i\left(\frac{dx^0}{ds}\right)^2+\Gamma^i_{jk}\frac{dx^j}{ds}\frac{dx^k}{ds}=0\tag{10}\end{equation}
ここで微小距離の式を簡略化します.\begin{eqnarray*}ds&=&\sqrt{g_{\mu\nu} dx^\mu dx^\nu}\\&=&\sqrt{(\eta_{\mu\nu}+h_{\mu\nu}) dx^\mu dx^\nu}\\&\approx&\sqrt{\eta_{\mu\nu} dx^\mu dx^\nu}\\&=&\sqrt{c^2dt^2-dx^2-dy^2-dz^2}\\&=& cdt\sqrt{1-\frac{v^2}{c^2}}\\&\approx& cdt\end{eqnarray*}最後の近似は非相対論極限 $\gamma\approx 1$ をとっています.
この結果より $ds=cdt=dx^0$ となるので測地線方程式(10)をさらに変形します.\begin{eqnarray*}&&\frac{d^2x^i}{ds^2}+\frac{1}{2}h_{00},_i\left(\frac{dx^0}{ds}\right)^2+\Gamma^i_{jk}\frac{dx^j}{ds}\frac{dx^k}{ds}=0\\\Leftrightarrow&& \frac{1}{c^2}\frac{d^2x^i}{dt^2}+\frac{1}{2}h_{00},_i+\Gamma^i_{jk}\frac{1}{c^2}\frac{dx^j}{dt}\frac{dx^k}{dt}=0\\\Leftrightarrow&& \frac{d^2x^i}{dt^2}+\frac{c^2}{2}h_{00},_i+\Gamma^i_{jk}\frac{dx^j}{dt}\frac{dx^k}{dt}=0\end{eqnarray*}第$2$項には $c^2$ があり,第$3$項は粒子の速度 $dx/dt$ の2次式となっていることから,非相対論的極限においては第$3$項を無視できます.従って$$\frac{d^2x^i}{dt^2}=-\frac{c^2}{2}h_{00},_i$$左辺は粒子の加速度ですから,両辺に質量 $m$ をかければニュートンの運動方程式の形になっています.$x^i$ は $x,y,z$ のことでしたから位置ベクトルを $\boldsymbol{r}$ として$$\frac{d^2\boldsymbol{r}}{dt^2}=-\frac{c^2}{2}\nabla h_{00}$$ニュートンの運動方程式はポテンシャルを $\phi$ として$$\frac{d^2\boldsymbol{r}}{dt^2}=-\nabla\phi$$ですから直前の式と比べれば$$\phi=\frac{c^2}{2}h_{00}+C$$無限遠で $\phi$ も $h_{00}$ も $0$ となるとすれば $C=0$ となります。よって$$h_{00}=\frac{2\phi}{c^2}$$従って$$g_{00}= 1+\frac{2\phi}{c^2}$$と対応させることができます.以上から,弱い定常重力場で非相対論的運動をする粒子の測地線はニュートンの運動方程式によって表せます.
時間成分の測地線方程式
$0$成分の方程式を吟味します.$$\frac{d^2x^0}{ds^2}+\Gamma^0_{\alpha\beta}\frac{dx^\alpha}{ds}\frac{dx^\beta}{ds}=0$$非相対論的極限で $cdt=dx^0=ds$ ですので左辺第1項は$0$となり$$\Gamma^0_{\alpha\beta}\frac{dx^\alpha}{dt}\frac{dx^\beta}{dt}=0$$先の議論で $\Gamma^0_{00}=0$ でしたから測地線方程式は$$2\Gamma^0_{i0}\frac{dx^i}{dt}\frac{dx^0}{dt}+\Gamma^0_{ij}\frac{dx^i}{dt}\frac{dx^j}{dt}=0$$
ここで\begin{eqnarray*}\Gamma^0_{i0}&=&\frac{1}{2}(\eta^{0\mu}+h^{0\mu})(h_{\mu i},_0+h_{\mu 0},_i-h_{0 i},_\mu)\\&\approx&\frac{1}{2}\eta^{0\mu}(h_{\mu i},_0+h_{\mu 0},_i-h_{0 i},_\mu)\\&=&\frac{1}{2}\eta^{0\mu}(h_{\mu 0},_i-h_{0 i},_\mu)\\&=&\frac{1}{2}\eta^{00}(h_{00},_i-h_{0 i},_0)\\&=&\frac{1}{2}h_{00},_i\\&=&\frac{1}{c^2}\frac{\partial \phi}{\partial x^i}\end{eqnarray*}
\begin{eqnarray*}\Gamma^0_{ij}&=&\frac{1}{2}g^{0\lambda}(g_{i\lambda},_j+g_{j\lambda},_i-g_{ij},_\lambda)\\&=&\frac{1}{2}g^{00}(g_{i0},_j+g_{j0},_i-g_{ij},_0)\\&=&0\end{eqnarray*}
これらのクリストッフェル記号を測地線方程式に適用します.\begin{eqnarray*}&&2\Gamma^0_{i0}\frac{dx^i}{dt}\frac{dx^0}{dt}+\Gamma^0_{ij}\frac{dx^i}{dt}\frac{dx^j}{dt}=0\\\Leftrightarrow&& 2c\Gamma^0_{i0}\frac{dx^i}{dt}+\Gamma^0_{ij}\frac{dx^i}{dt}\frac{dx^j}{dt}=0\\\Leftrightarrow&&\frac{2}{c}\frac{\partial \phi}{\partial x^i}\frac{dx^i}{dt}=0\\\Leftrightarrow&&\frac{\partial \phi}{\partial x^i}\frac{dx^i}{dt}=0\\\Leftrightarrow&&\frac{d\phi}{dt}=0\end{eqnarray*}これはポテンシャルが時間によって変化しないということであり,冒頭の仮定どおりです.なので$0$成分の測地線方程式を解くことでは特に新たな情報は得られませんでした.
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。