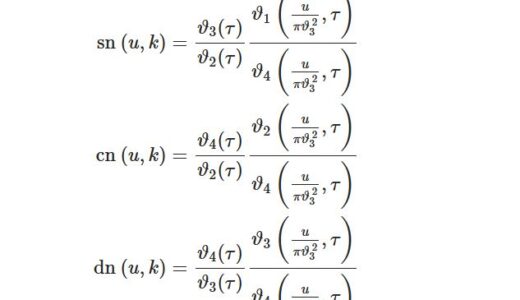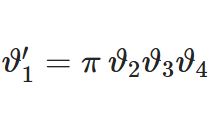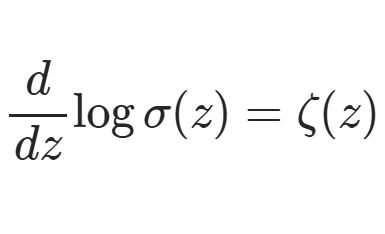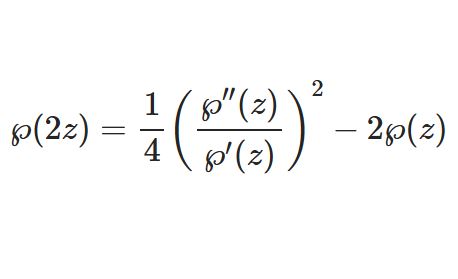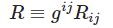\begin{equation}I_n(z)=\frac{1}{\pi}\int_0^\pi e^{z\cos\t}\cos n\t d\t\tag{1}\end{equation}\begin{equation}I_\nu(z)=\frac{1}{\sqrt{\pi}\G(\nu+\frac{1}{2})}\left(\frac{z}{2}\right)^\nu\int_0^\pi e^{\pm z\cos\t}\sin^{2\nu}d\t\tag{2}\end{equation}
ただし $I_\nu(z)$ は第1種変形ベッセル関数\begin{equation}I_\nu(z)=\sum_{m=0}^\infty\frac{1}{m!\G(m+\nu+1)}\left(\frac{z}{2}\right)^{2m+\nu}\tag{3}\end{equation}である.$\nu$ が整数 $n$ のときは$$I_{-n}(x)=I_n(x)$$変形ベッセル関数についての基本的な話は
を参照.また本稿の議論は第1種ベッセル関数 $J_\nu(z)$ の積分表示について論じた記事
と非常に類似している.
\begin{equation}e^{\frac{x}{2}(z+\frac{1}{z})}=\sum^{\infty}_{m=-\infty}I_m(x)z^m\tag{4}\end{equation}
左辺をローラン展開すると変形ベッセル関数が係数として現れるという意味の式である.左辺を $I_n(x)$ の母関数という.これを示す.\begin{eqnarray*} e^{\frac{x}{2}(z+\frac{1}{z})} &=& e^{\frac{x}{2}z}e^{\frac{x}{2z}}\\&=&\sum^\infty_{l=0}\frac{(\frac{x}{2}z)^l}{l!}\sum^\infty_{m=0}\frac{(\frac{x}{2z})^m}{m!}\\&=&\sum^\infty_{l=0}\sum^\infty_{m=0}\frac{1}{l!m!}\left(\frac{x}{2}\right)^{l+m}z^{l-m}\end{eqnarray*} $l\ge m$ のときと $l<m$ のときで分ける.\begin{equation} e^{\frac{x}{2}(z+\frac{1}{z})} = \sum^\infty_{l\ge m}\sum^\infty_{m=0} \frac{1}{l!m!}\left(\frac{x}{2}\right)^{l+m}z^{l-m} + \sum^\infty_{m>l}\sum^\infty_{l=0} \frac{1}{l!m!}\left(\frac{x}{2}\right)^{l+m}z^{l-m}\end{equation}第1項で $l=m+n$ , 第2項で $m=l+n$ とおくと \begin{eqnarray*} e^{\frac{x}{2}(z+\frac{1}{z})} &=& \sum^\infty_{n=0}\sum^\infty_{m=0} \frac{1}{(m+n)!m!}\left(\frac{x}{2}\right)^{2m+n}z^n + \sum^\infty_{n=1}\sum^\infty_{l=0} \frac{1}{l!(l+n)!}\left(\frac{x}{2}\right)^{2l+n}z^{-n}\\&=& \sum^\infty_{n=0} I_n(x)z^n+\sum^\infty_{n=1}I_n(x)z^{-n}\;\because(3)\\&=& \sum^\infty_{n=0} I_n(x)z^n+\sum^\infty_{n=1}I_{-n}(x)z^{-n}\\&=& \sum^\infty_{m=-\infty} I_m(x)z^m\end{eqnarray*} よって(4)が成立する.
(4)の 両辺に $z^{-n-1}$ をかけ,単位円 $|z|=1$ 上で複素積分する.$$\oint_{|z|=1}z^{-n-1}e^{\frac{x}{2}(z+\frac{1}{z})}dz= \sum^{\infty}_{m=-\infty}I_m(x)\oint_{|z|=1}z^{m-n-1}dz$$$z=e^{i\theta}$ と置換すると $dz=ie^{i\theta}d\theta$ であるから\begin{eqnarray*} &&\oint_{|z|=1}z^{-n-1}e^{\frac{x}{2}(z+\frac{1}{z})}dz= \sum^{\infty}_{m=-\infty}I_m(x)\oint_{|z|=1}z^{m-n-1}dz\\&\Leftrightarrow&\int^{2\pi}_0e^{-i(n+1)\theta}e^{x\frac{e^{i\theta}+e^{-i\theta}}{2}}ie^{i\theta}d\theta=\sum^{\infty}_{m=-\infty}I_m(x)\int^{2\pi}_0e^{i(m-n-1)\theta}ie^{i\theta}d\theta\\ &\Leftrightarrow& \int^{2\pi}_0e^{-in\theta}e^{x\cos\theta}d\theta=\sum^{\infty}_{m=-\infty}I_m(x)\int^{2\pi}_0e^{i(m-n)\theta}d\theta\\ &\Leftrightarrow& \int^{2\pi}_0e^{x\cos\theta-in\theta}d\theta=2\pi I_n(x)\end{eqnarray*}左辺については積分区間を半分に分けた後半のほうを$\phi=2\pi-\theta$ と置換することで\begin{eqnarray*} \int^{2\pi}_0e^{x\cos\theta-in\theta}d\theta&=& \int^{\pi}_0e^{x\cos\theta-in\theta}d\theta+ \int^{2\pi}_\pi e^{x\cos\theta-in\theta}d\theta\\&=&\int^{\pi}_0e^{x\cos\theta-in\theta}d\theta+ \int^{0}_{\pi}e^{x\cos\phi-in(2\pi-\phi)}(-d\phi)\\&=&\int^{\pi}_0e^{x\cos\theta-in\theta}d\theta+\int^{\pi}_{0}e^{x\cos\phi+in\phi}d\phi \\&=&2\int^{\pi}_0e^{x\cos\theta}\cos n\theta d\theta\end{eqnarray*} $$\therefore\quad I_n(x)=\frac{1}{\pi}\int^{\pi}_0e^{x\cos\theta}\cos n\theta d\theta$$よって(1)は示された.
次に(2)を示す.唐突であるが$$\int^1_{-1}e^{-zx}(1-x^2)^{\nu-\frac{1}{2}}dx$$なる積分を考える.
過去記事を参照すれば必ずしも唐突でないと分かる.第1種ベッセル関数 $J_\nu(z)$ について同様の積分表示を導出した際に$$\int^1_{-1}e^{izx}(1-x^2)^{\nu-\frac{1}{2}}dx$$なる積分を利用した.$i^nI_n(z)=J_n(iz)$ であることからこの積分において $z\to iz$ と置き換えたものが(2)を導くであろうと推測できる.
$e^X$のマクローリン展開を用いて\begin{eqnarray*} \int^1_{-1}e^{-zx}(1-x^2)^{\nu-\frac{1}{2}}dx &=& \int^1_{-1}\sum_{n=0}^\infty\frac{(-zx)^n}{n!}(1-x^2)^{\nu-\frac{1}{2}}dx \\&=&\sum_{n=0}^\infty\frac{(-z)^n}{n!} \int^1_{-1}x^n(1-x^2)^{\nu-\frac{1}{2}}dx\end{eqnarray*}最右辺の被積分関数は $n$ が奇数のとき奇関数であり,偶数のとき偶関数であるので $n=2m$ のみ考えればよい.\begin{eqnarray*} \int^1_{-1}e^{-zx}(1-x^2)^{\nu-\frac{1}{2}}dx &=& \sum_{m=0}^\infty\frac{(-z)^{2m}}{(2m)!}\cdot 2\int^1_0 x^{2m}(1-x^2)^{\nu-\frac{1}{2}}dx\\&=& \sum_{m=0}^\infty\frac{z^{2m}}{(2m)!}\cdot 2\int^1_0 x^{2m}(1-x^2)^{\nu-\frac{1}{2}}dx\\&=& \sum_{m=0}^\infty\frac{z^{2m}}{(2m)!}\int^1_0 y^{m}(1-y)^{\nu-\frac{1}{2}}\frac{dy}{\sqrt{y}}\\&=& \sum_{m=0}^\infty\frac{z^{2m}}{(2m)!}\int^1_0 y^{m-\frac{1}{2}}(1-y)^{\nu-\frac{1}{2}}dy\\&=& \sum_{m=0}^\infty\frac{z^{2m}}{(2m)!}B\left(m+\frac{1}{2},\nu+\frac{1}{2}\right)\\&=&\sum_{m=0}^\infty\frac{z^{2m}}{(2m)!}\frac{\Gamma(m+\frac{1}{2})\Gamma(\nu+\frac{1}{2})}{\Gamma(m+\nu+1)}\end{eqnarray*}ここでは置換 $x^2=y$ およびベータ関数の定義$$B(x,y)=\int_0^1t^{x-1}(1-t)^{y-1}dt$$およびベータ関数とガンマ関数の関係式$$B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$$を用いた.最後に現れたガンマ関数の1つを\begin{eqnarray*}\Gamma\left(m+\frac{1}{2}\right)&=&(m-\frac{1}{2})(m-\frac{3}{2})\cdots\frac{3}{2}\frac{1}{2}\Gamma\left(\frac{1}{2}\right)\\&=& (m-\frac{1}{2})(m-\frac{3}{2})\cdots\frac{3}{2}\frac{1}{2}\sqrt{\pi}\\&=& \frac{(2m-1)!!}{2^m}\sqrt{\pi}\end{eqnarray*}と変形を施せば\begin{eqnarray*} \int^1_{-1}e^{-zx}(1-x^2)^{\nu-\frac{1}{2}}dx &=& \sqrt{\pi}\sum_{m=0}^\infty\frac{z^{2m}}{(2m)!}\frac{(2m-1)!!}{2^m}\frac{\Gamma(\nu+\frac{1}{2})}{\Gamma(m+\nu+1)}\\&=& \sqrt{\pi}\Gamma(\nu+\frac{1}{2})\sum_{m=0}^\infty\frac{z^{2m}}{(2m)!!}\frac{1}{2^m}\frac{1}{\Gamma(m+\nu+1)}\\&=& \sqrt{\pi}\Gamma(\nu+\frac{1}{2})\sum_{m=0}^\infty\frac{z^{2m}}{m!2^{2m}}\frac{1}{\Gamma(m+\nu+1)}\\&=& \sqrt{\pi}\Gamma(\nu+\frac{1}{2})\sum_{m=0}^\infty\frac{1}{m!\Gamma(m+\nu+1)}\left(\frac{z}{2}\right)^{2m}\\&=& \frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(z/2)^\nu} \sum_{m=0}^\infty\frac{1}{m!\Gamma(m+\nu+1)}\left(\frac{z}{2}\right)^{2m+\nu}\\&=& \frac{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}{(z/2)^\nu} I_\nu(z) \quad\because(3)\end{eqnarray*}$$\therefore\quad I_\nu(z)=\frac{1}{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}\left(\frac{z}{2}\right)^\nu\int^1_{-1}e^{-zx}(1-x^2)^{\nu-\frac{1}{2}}dx$$
右辺の積分で $x=\cos\theta$ あるいは $x=-\cos\theta$ とおくと$$\int^1_{-1}e^{-zx}(1-x^2)^{\nu-\frac{1}{2}}=\int_0^\pi e^{\pm z\cos\theta}\sin^{2\nu}\theta d\theta$$となるから$$I_\nu(z)=\frac{1}{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}\left(\frac{z}{2}\right)^\nu\int_0^\pi e^{\pm z\cos\theta}\sin^{2\nu}\theta d\theta$$よって(2)は示された.
あるいは\begin{eqnarray*}I_\nu(z)&=&\frac{1}{2}I_\nu(z)+\frac{1}{2}I_\nu(z)\\&=&\frac{1}{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}\left(\frac{z}{2}\right)^\nu\int_0^\pi \frac{e^{z\cos\theta}+e^{-z\cos\theta}}{2}\sin^{2\nu}\theta d\theta\\&=&\frac{1}{\sqrt{\pi}\Gamma(\nu+\frac{1}{2})}\left(\frac{z}{2}\right)^\nu\int_0^\pi \cosh(z\cos\theta)\sin^{2\nu}\theta d\theta\end{eqnarray*}とも表せる.
\begin{equation}I_n(z)=\frac{1}{\pi}\int_0^\pi e^{z\cos\t}\cos n\t d\t\tag{1}\end{equation}\begin{equation}I_\nu(z)=\frac{1}{\sqrt{\pi}\G(\nu+\frac{1}{2})}\left(\frac{z}{2}\right)^\nu\int_0^\pi e^{\pm z\cos\t}\sin^{2\nu}d\t\tag{2}\end{equation}
特殊関数の記事
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。