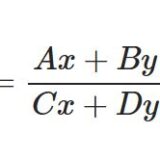球対称な密度分布をもつ流体の天体を考えます。例えば太陽のようなガスでできている恒星とか。恒星は中心の密度が一番高く、表面で密度ゼロです。
この星の内部で、半径 $r$ で厚さ $dr$ の球殻の部分を考えます。静水圧平衡すなわち、この球殻の流体にかかる力はゼロとすると、内側からの圧力 $P(r)$ による力、外側からの圧力 $P(r+dr)$ による力および万有引力を合計するとゼロですので\begin{equation}4\pi r^2 P(r+dr)+G\frac{(4\pi r^2\rho(r)dr)M(r)}{r^2}= 4\pi r^2 P(r)\tag{1}\end{equation}ただし $\rho(r)$ は半径 $r$ における流体の密度、$M(r)$ は中心から半径 $r$ の流体の質量を表します。左辺第2項の $(4\pi r^2\rho(r)dr)$ については、いま考えている球殻の体積 $4\pi r^2dr$ に密度 $\rho(r)$ をかけることで球殻の質量としたものです。(1)を変形して\begin{equation}P(r+dr)-P(r)=-G \frac{\rho(r)M(r)}{r^2}dr\tag{2}\end{equation}\begin{equation}\therefore\quad \frac{dP}{dr}=-G \frac{\rho(r)M(r)}{r^2}\tag{3}\end{equation}また球対称な密度と、半径 $r$ 以下の部分の質量の関係は\begin{equation}\frac{dM}{dr}=4\pi r^2\rho(r)\tag{4}\end{equation}
さて、ここで流体の圧力と密度がポリトロープ関係を満たすとします。すなわち定数 $K$ , $n$ があって\begin{equation}P(r)=K\rho(r)^{1+\frac{1}{n}}\tag{5}\end{equation}と書けるとします。(5)を微分すると\begin{equation}\frac{dP}{dr}=K\left(1+\frac{1}{n}\right)\rho^\frac{1}{n}\frac{d\rho}{dr}\tag{6}\end{equation}(3)と(6)から\begin{equation}K\left(1+\frac{1}{n}\right)\rho^\frac{1}{n}\frac{d\rho}{dr}=-G \frac{\rho(r)M(r)}{r^2}\tag{7}\end{equation}\begin{equation}\therefore\quad M(r)=-\frac{K}{G}\left(1+\frac{1}{n}\right)r^2\rho^{\frac{1}{n}-1}\frac{d\rho}{dr}\tag{8}\end{equation}(8)を微分して(4)を用いると\begin{equation}4\pi r^2\rho=-\frac{K}{G}\left(1+\frac{1}{n}\right)\frac{d}{dr}\left(r^2\rho^{\frac{1}{n}-1}\frac{d\rho}{dr}\right)\tag{9}\end{equation}ちょっと見づらいので変換しましょう。 $\rho_c:=\rho(0)$ として\begin{equation}\a:=\sqrt{\frac{(n+1)K\rho_c^{\frac{1}{n}-1}}{4\pi G}}\tag{10}\end{equation}なる定数 $\a$ を定義して\begin{equation}r=\a\xi\tag{11}\end{equation}と変数変換をします。$$\frac{d}{dr}=\frac{1}{\a}\frac{d}{d\xi}$$ですから(9)は\begin{equation}\xi^2\rho=-\frac{1}{n}\frac{1}{\rho_c^{\frac{1}{n}-1}}\frac{d}{d\xi}\left(\xi^2\rho^{\frac{1}{n}-1}\frac{d\rho}{d\xi}\right)\tag{12}\end{equation}$\rho=\rho_c\t^n$ と置くと\begin{equation}\frac{1}{\xi^2}\frac{d}{d\xi}\left(\xi^2\frac{d\t}{d\xi}\right)+\t^n=0\tag{13}\end{equation}と、まずまずシンプルな微分方程式になります。これをレーン・エムデン方程式といいます。あるいは\begin{equation}\xi^2\frac{d^2\t}{d\xi^2}+2\xi\frac{d\t}{d\xi}+\xi^2\t^n=0\tag{14}\end{equation}でもよいです。これまでの内容から $\t(0)=1$ です。またもう1つの境界条件として $\t'(0)=0$ を導入します。
レーン・エムデン方程式(13)or(14)は $n=0,1,5$ で解析的に解くことができます。
$n=0$ では(14)は $\t'=u$ に関する1階微分方程式\begin{equation}u'+\frac{2}{\xi}u=-1\tag{15}\end{equation}に帰着します。こちらの記事を参考にして$$\frac{1}{\xi^2}\frac{d}{d\xi}(\xi^2u)=u'+\frac{2}{\xi}u$$を(15)に適用すると$$u=\t'=-\frac{\xi}{3}+\frac{C}{\xi^2}$$となります。$\t'(0)=0$ なので $C=0$ でなくてはならず$$\t'=-\frac{\xi}{3}$$これを積分して $\t(0)=1$ より\begin{equation}\t=1-\frac{\xi^2}{6}\tag{16}\end{equation}と解けます。
次に $n=1$ においては(14)は\begin{equation}\xi^2\frac{d^2\t}{d\xi^2}+2\xi\frac{d\t}{d\xi}+\xi^2\t=0\tag{17}\end{equation}なる方程式となりますが、これは $0$ 次の球ベッセルの微分方程式であり、特殊解は球ベッセル関数 $j_0$ , $n_0$ です。よって一般解は\begin{equation}\t=c_1\frac{\sin\xi}{\xi}-c_2\frac{\cos\xi}{\xi}\tag{18}\end{equation}境界条件を適用すると\begin{equation}\t=\frac{\sin\xi}{\xi}\tag{19}\end{equation}
$n=5$ については他に参考となるサイトや文献があるのでご覧ください。ちょっと書く時間がないもので。。。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。