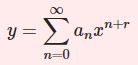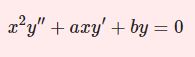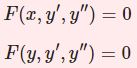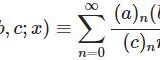基本的な合流型超幾何微分方程式の，フロベニウス法による解き方を解説する．ガウスの超幾何微分方程式と同様の手順であり，似た形の級数解を得る．一般的な解説＋３つの例題で学んでいこう．
級数法については
ガウスの超幾何微分方程式については
\begin{equation}xy^{\prime\prime}+(c-x)y'-ay=0\tag{1}\end{equation}
フロベニウス法によります．$$y=\sum_{n=0}^\infty a_nx^{n+r}\;(a_0\neq 0)$$とおくと$$y'= \sum_{n=0}^\infty (n+r)a_nx^{n+r-1}$$ $$y^{\prime\prime}= \sum_{n=0}^\infty (n+r)(n+r-1)a_nx^{n+r-2}$$となりますので(1)は\begin{equation}r(r-1+c)a_0x^{r-1}+\sum_{n=0}^\infty [(n+r+1)(n+r+c)a_{n+1}-(n+r+a)a_n]x^{n+r}=0\tag{2}\end{equation}左辺第1項より決定方程式$$r(r-1+c)=0$$$$\therefore\quad r=0\;,\;1-c$$この２つの $r$ がそれぞれ特殊解を導きます．
$r=0$ のときは$$y=\sum_{n=0}^\infty a_nx^{n}\;(a_0\neq 0)$$として計算し(2)を得れば$$(n+1)(n+c)a_{n+1}=(n+a)a_n\;(n\ge 0)$$となるから漸化式は$$a_{n+1}=\frac{n+a}{(n+1)(n+c)}a_n\;\;\;(a_0:任意)$$これを繰り返し用いて\begin{eqnarray*}a_n&=&\frac{n+a-1}{n(n+c-1)}a_{n-1}\\&\vdots&\\ &=&\frac{(n+a-1)(n+a-2)\cdots(a+1)a}{n!\cdot(n+c-1)(n+c-2)\cdots(c+1)c}a_0\\&=&\frac{(a)_n}{(c)_n}\frac{1}{n!}a_0\\&=& \frac{(a)_n}{(c)_n}\frac{1}{n!} \end{eqnarray*}ここで任意定数 $a_0=1$ としました．よって特殊解は$$y_1=\sum_{n=0}^\infty a_nx^n=\sum_{n=0}^\infty\frac{(a)_n}{(c)_n}\frac{x^n}{n!}$$簡単に表すために超幾何級数の分子が１つのバージョンを$${}_1F_1\left[\begin{matrix}a\\c\end{matrix}\;;x\right]\equiv \sum_{n=0}^\infty\frac{(a)_n}{(c)_n}\frac{x^n}{n!} $$と書くことにすると$$y_1(x)= {}_1F_1\left[\begin{matrix}a\\c\end{matrix}\;;x\right]$$ となりました！
上ではポッホハマー記号$$(X)_n\equiv X(X+1)(X+2)\cdots (X+n-1)$$をもちいました．なお $(X)_0=1$ と定めます．
$r=1-c$ のときは$$y=\sum_{n=0}^\infty a_nx^{n+1-c}\;(a_0\neq 0)$$として計算し(2)を得れば漸化式は$$a_{n+1}=\frac{n+a-c+1}{(n-c+2)(n+1)}a_n\;\;\;(a_0:任意)$$となりますので\begin{eqnarray*}a_n&=&\frac{n+a-c}{n(n-c+1)}a_{n-1}\\&\vdots&\\ &=&\frac{(n+a-c)(n+a-c-1)\cdots(a-c+1)}{n!\cdot(n-c+1)(n-c)\cdots(2-c)}a_0\\&=&\frac{(a-c+1)_n}{(2-c)_n}\frac{1}{n!}a_0\\&=& \frac{(a-c+1)_n}{(2-c)_n}\frac{1}{n!} \end{eqnarray*}ここで任意定数 $a_0=1$ としました．よって特殊解は$$y_2=\sum_{n=0}^\infty a_nx^{n+1-c}=x^{1-c}\sum_{n=0}^\infty\frac{(a-c+1)_n}{(2-c)_n}\frac{x^n}{n!}$$先ほどと同様の表記で書きます．$$\therefore\quad y_2(x)=x^{1-c} {}_1F_1\left[\begin{matrix}a-c+1\\2-c\end{matrix}\;;x\right]$$
以上より合流型超幾何微分方程式(1)の特殊解およびその線型結合である一般解は以下のようになります．
特殊解 $$\begin{cases}y_1(x)&=& {}_1F_1\left[\begin{matrix}a\\c\end{matrix}\;;x\right]\\ y_2(x)&=&x^{1-c} {}_1F_1\left[\begin{matrix}a-c+1\\2-c\end{matrix}\;;x\right] \end{cases}$$ 一般解$$y(x)=c_1\cdot {}_1F_1\left[\begin{matrix}a\\c\end{matrix}\;;x\right]+c_2\cdot x^{1-c} {}_1F_1\left[\begin{matrix}a-c+1\\2-c\end{matrix}\;;x\right]$$
以下で実践をやってみましょう．
級数解が得られたとしてもそれで終わりとは限りません．その解が既知の初等関数などと一致しないか確認を忘れないようにしましょう．
ただ例題を作るにあたって，両方の特殊解が初等関数で表せるようにするのがなかなかできませんでしたけど．
$$xy^{\prime\prime}+\left(\frac{1}{2}-x\right)y'-\frac{1}{2}y=0$$
$a=c=\frac{1}{2}$ です．よって$$y_1={}_1F_1\left[\begin{matrix}1/2\\1/2\end{matrix}\;;x\right]=\sum_{n=0}^\infty \frac{x^n}{n!} $$$$\therefore\quad y_1=e^x$$
$y_2$ はどうにもならないようです．よって一般解は$$ y(x)=c_1e^x+c_2\sqrt{x}\, {}_1F_1\left[\begin{matrix}1\\3/2\end{matrix}\;;x\right]$$
この方程式を変形すると$$x(y^{\prime\prime}-y')+\frac{1}{2}(y'-y)=0$$$z(x)=y-y'$ とおけば1階微分方程式に帰着してフロベニウス法が不要となります．$y_2$ は無理っぽいですけど．
$$xy^{\prime\prime}+\left(\frac{1}{2}-x\right)y'+2y=0$$
$a=-2$ , $c=1/2$ なので\begin{eqnarray*}y_1&=&{}_1F_1\left[\begin{matrix}-2\\1/2\end{matrix}\;;x\right]\\&=& \sum_{n=0}^\infty \frac{(-2)_n}{(\frac{1}{2})_n}\frac{x^n}{n!}\\&=& 1-4x+\frac{4}{3}x^2\end{eqnarray*}$(-2)_n$ は $n\ge 3$ でゼロとなるので多項式になります．
またしても $y_2$ はどうにもならないようです．ラゲール陪函数という特殊関数で表せるようですがやめておきます．一般解は$$y(x)=c_1\left(1-4x+\frac{4}{3}x^2 \right)+ c_2\sqrt{x}\, {}_1F_1\left[\begin{matrix}-3/2\\3/2\end{matrix}\;;x\right]$$
$$xy^{\prime\prime}+(2-x)y'-y=0$$
$a=1$ , $c=2$ です．\begin{eqnarray*} y_1&=&{}_1F_1\left[\begin{matrix}1\\2\end{matrix}\;;x\right]\\&=& \sum_{n=0}^\infty \frac{n!}{(n+1)!}\frac{x^n}{n!}\\&=&\frac{1}{x}\sum_{n=0}^\infty \frac{x^{n+1}}{(n+1)!}\\ &=&\frac{e^x-1}{x}\end{eqnarray*}と初等的に表せました．
\begin{eqnarray*} y_2&=&\frac{1}{x}{}_1F_1\left[\begin{matrix}0\\0\end{matrix}\;;x\right]\\&=& \frac{1}{x}\sum_{n=0}^\infty \frac{(0)_n}{(0)_n}\frac{x^n}{n!}\\ &=&\frac{1}{x}\end{eqnarray*}ポッホハマー記号の定義では $(X)_0=1$ なので $(0)_0=1$ ですが，$n\ge 1$ では $(0)_n$ はまず初めに $0$ をかけるため値は $0$ です．
一般解は$$y(x)=\frac{c_1+c_2e^x}{x}$$
$y_2$ のほうの計算に自信が持てなかったので原点に立ち返ってフロベニウス法$$y=\sum_{n=0}^\infty a_nx^{n-1}=\frac{a_0}{x}+\sum_{n=0}^\infty a_{n+1}x^n$$を試しました．
すると $a_0$ , $a_1$ は任意で$$a_{n+1}=\frac{1}{(n+1)!}a_1\quad(n\ge 1)$$なる漸化式を得ます．よって$$y_2=\frac{a_0}{x}+a_1\frac{e^x-1}{x}$$となります．ゆえに上と同じ形の一般解を得ますので正解だったというわけです．
次の記事：
常微分方程式シリーズ
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
