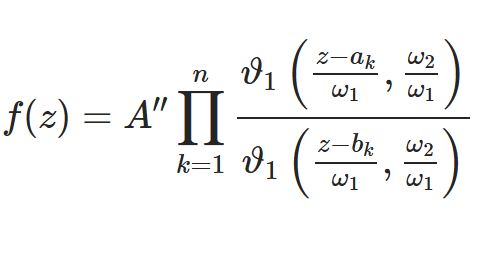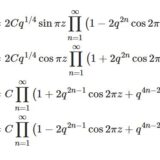前回はこちら:
テータ関数の導関数をつくりましょう。こちらの命題7より\begin{align}\vartheta_1(z) &= 2\sum_{n=0}^{\infty}(-1)^n q^{(n+\frac{1}{2})^2}\sin(2n+1)\pi z\tag{1a}\\\vartheta_2(z) &=2\sum_{n=0}^{\infty} q^{(n+\frac{1}{2})^2}\cos(2n+1)\pi z\tag{1b}\\\vartheta_3(z) &=1+2\sum_{n=1}^\infty q^{n^2}\cos2\pi nz\tag{1c}\\\vartheta_4(z) &=1+2\sum_{n=1}^\infty (-1)^nq^{n^2}\cos2\pi nz\tag{1d}\end{align}級数は広義一様収束するので項別微分すると導関数を得ます。
\begin{align}\vartheta_1'(z) &= 2\pi\sum_{n=0}^{\infty}(-1)^n(2n+1) q^{(n+\frac{1}{2})^2}\cos(2n+1)\pi z\tag{2a}\\\vartheta_2'(z) &=-2\pi\sum_{n=0}^{\infty} (2n+1)q^{(n+\frac{1}{2})^2}\sin(2n+1)\pi z\tag{2b}\\\vartheta_3'(z) &=-4\pi\sum_{n=1}^\infty nq^{n^2}\sin 2\pi nz\tag{2c}\\\vartheta_4'(z) &=-4\pi\sum_{n=1}^\infty (-1)^nnq^{n^2}\sin 2\pi nz\tag{2d}\end{align}\begin{align}\vartheta_1''(z) &= -2\pi^2\sum_{n=0}^{\infty}(-1)^n(2n+1)^2 q^{(n+\frac{1}{2})^2}\sin(2n+1)\pi z\tag{3a}\\\vartheta_2''(z) &=-2\pi^2\sum_{n=0}^{\infty} (2n+1)^2q^{(n+\frac{1}{2})^2}\cos(2n+1)\pi z\tag{3b}\\\vartheta_3''(z) &=-8\pi^2\sum_{n=1}^\infty n^2q^{n^2}\cos 2\pi nz\tag{3c}\\\vartheta_4''(z) &=-8\pi^2\sum_{n=1}^\infty (-1)^nn^2q^{n^2}\cos 2\pi nz\tag{3d}\end{align}
また前回導出したテータ関数の無限積表示からも導関数が得られます。無限積表示は次のようになるのでした:\begin{align}\vartheta_1(z)&=2Cq^{1/4}\sin\pi z\prod_{n=1}^\infty\left(1-2q^{2n}\cos 2\pi z+q^{4n}\right)\tag{4a}\\\vartheta_2(z)&=2Cq^{1/4}\cos\pi z\prod_{n=1}^\infty\left(1+2q^{2n}\cos 2\pi z+q^{4n}\right)\tag{4b}\\\vartheta_3(z)&=C\prod_{n=1}^\infty\left(1+2q^{2n-1}\cos 2\pi z+q^{4n-2}\right)\tag{4c}\\\vartheta_4(z)&=C\prod_{n=1}^\infty\left(1-2q^{2n-1}\cos 2\pi z+q^{4n-2}\right)\tag{4d}\end{align}ただし$$C=\prod_{n=1}^\infty (1-q^{2n})$$です。こちらの定理6.8により(4a)~(4d)の無限積は広義一様収束して解析関数となっています。このとき高校数学の「積の微分法則」と同じように微分できます。詳細はこちらの定理7.3を見てください。
すると(4c)の微分は\begin{equation}\vartheta_3'(z)=2\pi i\vartheta_3(z)\sum_{n=1}^\infty\left(\frac{q^{2n-1}e^{2\pi iz}}{1+q^{2n-1}e^{2\pi iz}}-\frac{q^{2n-1}e^{-2\pi iz}}{1+q^{2n-1}e^{-2\pi iz}}\right)\tag{5}\end{equation}さらに微分して\begin{align}\vartheta_3''(z)&=2\pi i\vartheta_3'(z)\sum_{n=1}^\infty\left(\frac{q^{2n-1}e^{2\pi iz}}{1+q^{2n-1}e^{2\pi iz}}-\frac{q^{2n-1}e^{-2\pi iz}}{1+q^{2n-1}e^{-2\pi iz}}\right)\\&\quad +(2\pi i)^2\vartheta_3(z)\sum_{n=1}^\infty\left(\frac{q^{2n-1}e^{2\pi iz}}{(1+q^{2n-1}e^{2\pi iz})^2}+\frac{q^{2n-1}e^{-2\pi iz}}{(1+q^{2n-1}e^{-2\pi iz})^2}\right)\tag{6}\end{align}となります。
$\vartheta_4(z)=\vartheta_3(z+\frac{1}{2})$ を使って $\vartheta_4(z)$ の導関数もすぐに得られます。
次に(4b)(4a)を見ましょう。$\cos$ や $\sin$ のせいで微分を書き下すのが面倒なので$$\a(z):=2Cq^{1/4}\prod_{n=1}^\infty\left(1+2q^{2n}\cos 2\pi z+q^{4n}\right)$$としておきます。すると$$\vartheta_2(z)=\cos\pi z\;\a(z)\;,\;\vartheta_1(z)=\vartheta_2\left(z-\frac{1}{2}\right)$$です。$\a(z)$ の微分は $\vartheta_3(z)$ の微分とほとんど同じであって\begin{align}\a'(z)&=2\pi i\a(z)\sum_{n=1}^\infty\left(\frac{q^{2n}e^{2\pi iz}}{1+q^{2n}e^{2\pi iz}}-\frac{q^{2n}e^{-2\pi iz}}{1+q^{2n}e^{-2\pi iz}}\right)\tag{7}\\\a''(z)&=2\pi i\a'(z)\sum_{n=1}^\infty\left(\frac{q^{2n}e^{2\pi iz}}{1+q^{2n}e^{2\pi iz}}-\frac{q^{2n}e^{-2\pi iz}}{1+q^{2n}e^{-2\pi iz}}\right)\\&\quad +(2\pi i)^2\a(z)\sum_{n=1}^\infty\left(\frac{q^{2n}e^{2\pi iz}}{(1+q^{2n}e^{2\pi iz})^2}+\frac{q^{2n}e^{-2\pi iz}}{(1+q^{2n}e^{-2\pi iz})^2}\right)\tag{8}\end{align}また\begin{equation}\a\left(z-\frac{1}{2}\right)=2Cq^{1/4}\prod_{n=1}^\infty\left(1-2q^{2n}\cos 2\pi z+q^{4n}\right)\tag{9}\end{equation}であることもおさえておきます。以上で(4a)(4b)の微分も得られます。
\begin{align}\vartheta_3'(z)&=2\pi i\vartheta_3(z)\sum_{n=1}^\infty\left(\frac{q^{2n-1}e^{2\pi iz}}{1+q^{2n-1}e^{2\pi iz}}-\frac{q^{2n-1}e^{-2\pi iz}}{1+q^{2n-1}e^{-2\pi iz}}\right)\\\vartheta_4'(z)&=2\pi i\vartheta_4(z)\sum_{n=1}^\infty\left(-\frac{q^{2n-1}e^{2\pi iz}}{1-q^{2n-1}e^{2\pi iz}}+\frac{q^{2n-1}e^{-2\pi iz}}{1-q^{2n-1}e^{-2\pi iz}}\right)\end{align}
\begin{align}\vartheta_3''(z)&=2\pi i\vartheta_3'(z)\sum_{n=1}^\infty\left(\frac{q^{2n-1}e^{2\pi iz}}{1+q^{2n-1}e^{2\pi iz}}-\frac{q^{2n-1}e^{-2\pi iz}}{1+q^{2n-1}e^{-2\pi iz}}\right)\\&\quad +(2\pi i)^2\vartheta_3(z)\sum_{n=1}^\infty\left(\frac{q^{2n-1}e^{2\pi iz}}{(1+q^{2n-1}e^{2\pi iz})^2}+\frac{q^{2n-1}e^{-2\pi iz}}{(1+q^{2n-1}e^{-2\pi iz})^2}\right)\\\vartheta_4''(z)&=2\pi i\vartheta_4'(z)\sum_{n=1}^\infty\left(-\frac{q^{2n-1}e^{2\pi iz}}{1-q^{2n-1}e^{2\pi iz}}+\frac{q^{2n-1}e^{-2\pi iz}}{1-q^{2n-1}e^{-2\pi iz}}\right)\\&\quad +(2\pi i)^2\vartheta_4(z)\sum_{n=1}^\infty\left(-\frac{q^{2n-1}e^{2\pi iz}}{(1-q^{2n-1}e^{2\pi iz})^2}-\frac{q^{2n-1}e^{-2\pi iz}}{(1-q^{2n-1}e^{-2\pi iz})^2}\right)\end{align}また(7)(8)を用いることで\begin{align}\vartheta_2'(z)&=-\pi\sin\pi z\;\a(z)+\cos\pi z\;\a'(z)\\\vartheta_1'(z)&=\pi\cos\pi z\;\a\left(z-\frac{1}{2}\right)+\sin\pi z\;\a'\left(z-\frac{1}{2}\right)\end{align}\begin{align}\vartheta_2''(z)&=-\pi^2\cos\pi z\;\a(z)-2\pi\sin\pi z\;\a'(z)+\cos\pi z\;\a''(z)\\\vartheta_1''(z)&=-\pi^2\sin\pi z\;\a\left(z-\frac{1}{2}\right)+2\pi\cos\pi z\;\a'\left(z-\frac{1}{2}\right)+\sin\pi z\;\a''\left(z-\frac{1}{2}\right)\end{align}
$z=0$ とすることで各種テータ定数を得ましょう。まず(4a)~(4d)により\begin{align}\vartheta_1&=0\tag{10a}\\\vartheta_2&=2Cq^{1/4}\left[\prod_{n=1}^\infty\left(1+q^{2n}\right)\right]^2\tag{10b}\\\vartheta_3&=C\left[\prod_{n=1}^\infty\left(1+q^{2n-1}\right)\right]^2\tag{10c}\\\vartheta_4&=C\left[\prod_{n=1}^\infty\left(1-q^{2n-1}\right)\right]^2\tag{10d}\end{align}定理2から導関数のテータ定数を計算します。$\a'(0)=0$ , $\a'(-1/2)=0$ および\begin{align}\a''(0)&=-8\pi^2\vartheta_2\sum_{n=1}^\infty\frac{q^{2n}}{(1+q^{2n})^2}\tag{11a}\\\a''(-1/2)&=8\pi\vartheta'_1\sum_{n=1}^\infty\frac{q^{2n}}{(1-q^{2n})^2}\tag{11b}\end{align}を準備しておけば
\begin{align}\vartheta_1' &= 2\pi q^{1/4}C^3\\\vartheta_2' &= 0\\\vartheta_3' &= 0\\\vartheta_4' &= 0\end{align}\begin{align}\vartheta_1'' &=0\\\vartheta_2'' &= -\pi^2\vartheta_2\left[1+8\sum_{n=1}^\infty\frac{q^{2n}}{(1+q^{2n})^2}\right]\\\vartheta_3'' &= -8\pi^2\vartheta_3\sum_{n=1}^\infty\frac{q^{2n-1}}{(1+q^{2n-1})^2}\\\vartheta_4'' &= 8\pi^2\vartheta_4\sum_{n=1}^\infty\frac{q^{2n-1}}{(1-q^{2n-1})^2}\end{align}
値がゼロになっているところについては、$\vartheta_1(z)$ が奇関数で $\vartheta_2(z)$,$\vartheta_3(z)$,$\vartheta_4(z)$ が偶関数であることを思い起こすと納得です。
ついでに後ほど使うので3階導関数のテータ定数も1つだけ導いておきます。
$$\vartheta_1'''=\pi^2\vartheta_1'\left[24\sum_{n=1}^\infty\frac{q^{2n}}{(1-q^{2n})^2}-1\right]$$
定理3'より\begin{equation}\frac{\vartheta_1'''}{\vartheta_1'}=\pi^2\left[24\sum_{n=1}^\infty\frac{q^{2n}}{(1-q^{2n})^2}-1\right]\tag{12}\end{equation}その一方で定理3から$$\pi^2+\frac{\vartheta_2''}{\vartheta_2}+\frac{\vartheta_3''}{\vartheta_3}+\frac{\vartheta_4''}{\vartheta_4}=-8\pi^2\left[\sum_{n=1}^\infty\frac{q^{2n}}{(1+q^{2n})^2}+\sum_{n=1}^\infty\frac{q^{2n-1}}{(1+q^{2n-1})^2}-\sum_{n=1}^\infty\frac{q^{2n-1}}{(1-q^{2n-1})^2}\right]$$右辺の級数のうちはじめの2つを足し合わせると$$=-8\pi^2\left[\sum_{n=1}^\infty\frac{q^{n}}{(1+q^{n})^2}-\sum_{n=1}^\infty\frac{q^{2n-1}}{(1-q^{2n-1})^2}\right]$$一番右の級数は $2n-1$ を足しているので、自然数全体で和をとったものから偶数の分を引けばよいです。よって$$=-8\pi^2\left[\sum_{n=1}^\infty\frac{q^{n}}{(1+q^{n})^2}-\sum_{n=1}^\infty\frac{q^{n}}{(1-q^{n})^2}+\sum_{n=1}^\infty\frac{q^{2n}}{(1-q^{2n})^2}\right]$$3つの級数のうちはじめの2つを普通に計算(通分)して$$=-8\pi^2\left[\sum_{n=1}^\infty\frac{-4q^{2n}}{(1-q^{2n})^2}+\sum_{n=1}^\infty\frac{q^{2n}}{(1-q^{2n})^2}\right]$$最終的に\begin{equation}\pi^2+\frac{\vartheta_2''}{\vartheta_2}+\frac{\vartheta_3''}{\vartheta_3}+\frac{\vartheta_4''}{\vartheta_4}=24\pi^2\sum_{n=1}^\infty\frac{q^{2n}}{(1-q^{2n})^2}\tag{13}\end{equation}(12)(13)を合わせて\begin{equation}\frac{\vartheta_1'''}{\vartheta_1'}=\frac{\vartheta_2''}{\vartheta_2}+\frac{\vartheta_3''}{\vartheta_3}+\frac{\vartheta_4''}{\vartheta_4}\tag{14}\end{equation}こちらの例5より\begin{equation}\vartheta_k''(z,\tau)=4\pi i\frac{\partial\vartheta_k(z,\tau)}{\partial\tau}\tag{15}\end{equation}ただしこれまでの表記に沿うように $z$ による微分を $'$ で表しています。(15)をさらに $z$ によって微分します。\begin{equation}\vartheta_k'''(z,\tau)=4\pi i\frac{\partial\vartheta_k'(z,\tau)}{\partial\tau}\tag{16}\end{equation}(15)(16)を(14)に適用すると$$\frac{1}{\vartheta_1'(0,\tau)}\frac{\partial\vartheta_1'(0,\tau)}{\partial\tau}=\frac{1}{\vartheta_2(0,\tau)}\frac{\partial\vartheta_2(0,\tau)}{\partial\tau}+\frac{1}{\vartheta_3(0,\tau)}\frac{\partial\vartheta_3(0,\tau)}{\partial\tau}+\frac{1}{\vartheta_4(0,\tau)}\frac{\partial\vartheta_4(0,\tau)}{\partial\tau}$$これを $\tau$ で積分すると(初等的. $\log$ になる)定数 $A$ を用いて$$\vartheta_1'(0,\tau)=A\vartheta_2(0,\tau)\vartheta_3(0,\tau)\vartheta_4(0,\tau)$$これまでどおり $\tau$ は省略することにすると$$\vartheta_1'=A\vartheta_2\vartheta_3\vartheta_4$$(1b)(1c)(1d)および(2a)から、$q\to 0$ によって\begin{align}q^{-1/4}\vartheta_1'&=2\pi \sum_{n=0}^\infty (-1)^n(2n+1)q^{n(n+1)}\rightarrow 2\pi\\q^{-1/4}\vartheta_2&=2\sum_{n=0}^\infty q^{n(n+1)}\rightarrow 2\\\vartheta_3 &=1+2\sum_{n=1}^\infty q^{n^2}\rightarrow 1\\\vartheta_4 &=1+2\sum_{n=1}^\infty (-1)^nq^{n^2}\rightarrow 1\end{align}なので $A=\pi$ となります。結局
$$\vartheta_1'=\pi\: \vartheta_2\vartheta_3\vartheta_4$$
ここまで定数 $C$ の値を導出せずにいましたが、定理4は $C$ の値が分からなくても得られます。そこで定理4から $C$ を求めましょう。
定理4右辺に(10b)(10c)(10d)を用います。左辺の $\vartheta_1'$ については$$\vartheta_1'=2\pi Cq^{1/4}\prod_{n=1}^\infty (1-q^{2n})^2$$を使います(定理3の第1式を使いたいところですが、$C=\prod (1-q^{2n})$ を使用してしまっているのでダメ)。すると$$\left(\prod_{n=1}^\infty (1-q^{2n})\right)^2=C^2\left(\prod_{n=1}^\infty(1+q^{2n})\prod_{n=1}^\infty(1+q^{2n-1})\prod_{n=1}^\infty(1-q^{2n-1})\right)^2$$右辺の無限積のうちはじめの2つをまとめます。最後の無限積はその逆。$$\left(\prod_{n=1}^\infty (1-q^{2n})\right)^2=C^2\left(\prod_{n=1}^\infty(1+q^{n})\prod_{n=1}^\infty\frac{1-q^{n}}{1-q^{2n}}\right)^2$$右辺を整理して$$\left(\prod_{n=1}^\infty (1-q^{2n})\right)^2=C^2$$このままだと $C$ の符号 $\pm$ が定まりませんが、$q\to 0$ としたときの $\vartheta_3$ の値を見ることにより、
$$C=\prod_{n=1}^\infty (1-q^{2n})$$
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

つぎはこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。