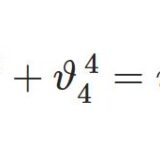前回はこちら:
今回からは楕円関数の話の続きとして、テータ関数を学んでいきます。
もくじ
定義の方法にはいくつか流儀があるようですが、MumfordのTata lectures on thetaという書籍で採用されているらしいものを選びました。
$\tau\in\CC$ を $\mathfrak{I}(\tau)>0$ を満たす定数とします。すなわち $\tau=a+bi$ とおくと $b>0$ ということ。
さらに $q:=e^{\pi i\tau}$ とおきます。すると$$|q|=e^{-\pi b} <1$$であることが分かります。
さてスタートとなる $z$ の関数を
$z,\tau\in\CC$ , $\mathfrak{I}(\tau)>0$, \begin{equation}\vartheta(z,\tau):=\sum_{n=-\infty}^{+\infty}e^{\pi in^2\tau+2\pi inz}\tag{1}\end{equation}
と定義します。あるいは\begin{equation}\vartheta(z;q)=\sum_{n=-\infty}^{+\infty}q^{n^2}e^{2\pi inz}\tag{2}\end{equation}とも書きます。この $\vartheta$ をテータ関数といいます。
上述の通りテータ関数は $z$ に関する関数項級数として定義されています。複素平面において $|z|\le R$ の範囲においては$$|q^{n^2}e^{2\pi inz}|=|q|^{n^2}e^{-2\pi n\mathfrak{I}(z)}\le |q|^{n^2}e^{2\pi nR}$$これは正確に言えば $n>0$ だけで成り立つ式ですが、$n<0$ の場合も同様に議論できます。
ダランベールの収束判定法を使いましょう。\begin{equation}\frac{|q|^{(n+1)^2}e^{2\pi (n+1)R}}{|q|^{n^2}e^{2\pi nR}}=|q|^{2n+1}e^{2\pi R}\xrightarrow[]{n\to +\infty}0\tag{3}\end{equation}で判定結果は「収束」です。\begin{equation}\sum_{n=-\infty}^{+\infty}\left|q^{n^2}e^{2\pi inz}\right|\le\sum_{n=-\infty}^{+\infty}|q|^{n^2}e^{2\pi nR}\tag{4}\end{equation}なのですから、(4)の右辺が(3)の結果により収束することから(4)の左辺も収束します。
したがって(2)の級数は $|z|\le R$ で $z$ に無関係に収束することから、$|z|\le R$ で一様収束しています。$R$ は任意ですので、結局この級数は $\CC$ 上で広義一様収束します。
また絶対収束でもあるので、級数の和をとる順序は自由です。
広義一様収束することから、$z$ の関数であるテータ関数 $\vartheta(z,\tau)$ は全平面で解析的であり、整関数ということになります。
テータ関数 $\vartheta(z,\tau)$ は整関数である。
テータ関数は周期をもちます。しかし整関数であることから二重周期をもつことはありえず、楕円関数ではありません。
より具体的に見てみましょう。定義(1)よりただちに\begin{equation}\vartheta(z+1,\tau)=\vartheta(z,\tau)\tag{5}\end{equation}よってテータ関数は周期 $1$ をもちます。
また同じく定義(1)より\begin{align}\vartheta(z+\tau,\tau) &=\sum_{n=-\infty}^{+\infty}e^{\pi in^2\tau+2\pi inz+2\pi in\tau} \\&= \sum_{n=-\infty}^{+\infty}e^{\pi i(n+1)^2\tau-\pi i\tau +2\pi i(n+1)z-2\pi iz}\\&= e^{-\pi i\tau-2\pi iz}\sum_{n=-\infty}^{+\infty}e^{\pi i(n+1)^2\tau+2\pi i(n+1)z}\\&=e^{-\pi i\tau-2\pi iz}\sum_{n=-\infty}^{+\infty}e^{\pi in^2\tau+2\pi inz}\\ &=e^{-\pi i\tau-2\pi iz}\vartheta(z,\tau)\tag{6}\end{align}$\tau$ は周期ではないものの関数の一定の変化を特徴づけるものであり、擬周期性といいます。1方向に周期をもち、もう1方向にはこのような擬周期をもつのはワイエルシュトラスのシグマ関数と似ています。
この周期性を繰り返し用いると\begin{align}\vartheta(z+m\tau+n,\tau)&=\vartheta(z+m\tau,\tau)\\&=e^{-2\pi i(m-\frac{1}{2})\tau-2\pi iz}\vartheta(z+(m-1)\tau,\tau)\\&=e^{-2\pi i(m-\frac{1}{2})\tau-2\pi iz}e^{-2\pi i(m-\frac{3}{2})\tau-2\pi iz}\vartheta(z+(m-2)\tau,\tau)\\&\quad\vdots\\&=e^{-\pi im^2\tau-2\pi imz}\vartheta(z,\tau)\end{align}
\begin{align}\vartheta(z+1,\tau)&=\vartheta(z,\tau)\\\vartheta(z+\tau,\tau) &=e^{-\pi i\tau-2\pi iz}\vartheta(z,\tau)\end{align}またこれらより $m,n\in\NN$ で$$\vartheta(z+m\tau+n,\tau)=e^{-\pi im^2\tau-2\pi imz}\vartheta(z,\tau)$$
定理3より$$\left|\frac{\vartheta(z+m\tau+n,\tau)}{\vartheta(z,\tau)}\right|=e^{\pi m^2\mathfrak{I}(\tau)+2\pi m\mathfrak{I}(z)}$$よって $m$ が大きくなる場合に発散します。テータ関数は整関数でしたから発散するとしたらそこは無限遠点です。
$\vartheta(z,\tau)$ は有界ではなく、無限遠で発散する。
ちなみにテータ関数は整関数なので、リウヴィルの定理を使えば有界ではないことがすぐに分かります。
テータ関数は $\vartheta(z,\tau)$ を基本としていくつかの類似したものが用いられます。
2つの添え字 $a,b\in\RR$ がついたテータ関数を次で定義します。
$z,\tau\in\CC$ , $\mathfrak{I}(\tau)>0$, $$\vartheta_{ab}(z,\tau):=\sum_{n=-\infty}^{+\infty}e^{\pi i(n+\frac{a}{2})^2\tau+2\pi i(n+\frac{a}{2})(z+\frac{b}{2})}$$
これも同様に $z$ の関数として見ます。
まず明らかに\begin{equation}\vartheta_{00}(z,\tau)=\vartheta(z,\tau)\tag{7}\end{equation}わずかな計算により次もすぐに分かります:\begin{align}\vartheta_{01}(z,\tau)&=\vartheta\left(z+\frac{1}{2},\tau\right)=\sum_{n=-\infty}^{+\infty}(-1)^ne^{\pi in^2\tau+2\pi inz}\tag{8}\\\vartheta_{10}(z,\tau)&=e^{\frac{\pi i}{4}\tau+\pi iz}\;\vartheta\left(z+\frac{\tau}{2},\tau\right)\tag{9}\\\vartheta_{11}(z,\tau)&=e^{\frac{\pi i}{4}\tau+\pi i(z+\frac{1}{2})}\;\vartheta\left(z+\frac{1+\tau}{2},\tau\right)\tag{10}\end{align}(8)~(10)は(7)の $z$ を半周期ずらした感じのものになっています。添え字11と10,01の関係についても\begin{align}\vartheta_{11}(z,\tau)&=\vartheta_{10}\left(z+\frac{1}{2},\tau\right)\tag{10'a}\\\vartheta_{11}(z,\tau)&=e^{\frac{\pi i}{4}\tau+\pi i(z+\frac{1}{2})}\vartheta_{01}\left(z+\frac{\tau}{2},\tau\right)\end{align}
添え字が0,1しか登場していませんが、20とか02は1周期分ずらすだけですから特に必要ありません。非整数の添え字もあるかもしれませんが、ここではとりあげません。
さらに(7)~(10)は慣習的に次のように書かれます。
\begin{align}\vartheta_1(z,\tau)&:=-\vartheta_{11}(z,\tau)\\\vartheta_2(z,\tau)&:=\vartheta_{10}(z,\tau)\\\vartheta_3(z,\tau)&:=\vartheta_{00}(z,\tau)\\\vartheta_4(z,\tau)&:=\vartheta_{01}(z,\tau)\end{align}
これら4つのテータ関数は、その定義から分かるように元のテータ関数 $\vartheta$ の性質を(ある程度)引き継いでいます。すなわち(擬)周期 $1$ および擬周期 $\tau$ をもつことと(後述)、整関数であることです。
なお $q=e^{\pi i\tau}$ を使う場合に $\vartheta(z,\tau)$ を $\vartheta(z;q)$ と書いたのと同様に、添え字が付いたテータ関数それぞれでも $\theta_i(z;q)$ と書く場合があります。
$q=e^{\pi i\tau}$ を使うことにします。$$\sum_{n=-\infty}^{+\infty}a_n=a_0+\sum_{n=-\infty}^{-1}a_n+\sum_{n=1}^{+\infty}a_n$$であることから(2)は\begin{equation}\vartheta(z;q)=1+2\sum_{n=1}^\infty q^{n^2}\cos2\pi nz\tag{11}\end{equation}と書けます。また定義5からスタートして\begin{align}\vartheta_{10}(z;q) &=\sum_{n=-\infty}^{+\infty}q^{(n+\frac{1}{2})^2}e^{(2n+1)\pi iz}\\&=2\sum_{n=0}^{+\infty}q^{(n+\frac{1}{2})^2}\cos(2n+1)\pi z\tag{12}\end{align}のように書けることも分かります(最後の等号は実際に総和を何項か書き出して確認できる)。
このようにしていけば、次のようにまとめられます。
\begin{align}\vartheta_1(z;q) &= -\vartheta_{11}(z;q)\\&=2\sum_{n=0}^{\infty}(-1)^n q^{(n+\frac{1}{2})^2}\sin(2n+1)\pi z\\\vartheta_2(z;q) &= \vartheta_{10}(z;q)\\&=2\sum_{n=0}^{\infty} q^{(n+\frac{1}{2})^2}\cos(2n+1)\pi z\\\vartheta_3(z;q) &= \vartheta_{00}(z;q)\\&=1+2\sum_{n=1}^\infty q^{n^2}\cos2\pi nz\\\vartheta_4(z;q) &= \vartheta_{01}(z;q)\\&=1+2\sum_{n=1}^\infty (-1)^nq^{n^2}\cos2\pi nz\end{align}
これをみるとつぎが分かります。
$\vartheta_1(z;q)$ は奇関数、$\vartheta_2(z;q)$,$\vartheta_3(z;q)$,$\vartheta_4(z;q)$ は偶関数である。
パラメータ $\tau$ は基本的に固定されているので、単に $\vartheta(z)$ のように書くこともあります。添え字が付く場合でも同様です。
また $z=0$ の値を $\vartheta_1:=\vartheta_1(0)$ のように書いてテータ定数といいます。導関数もこれに倣って $\vartheta'_1:=\vartheta'_1(0)$ のように書きます。
次を示せ:\begin{align}\vartheta_3(2z;q^4)+\vartheta_2(2z;q^4)&= \vartheta_3(z;q)\\\vartheta_3(2z;q^4)-\vartheta_2(2z;q^4)&= \vartheta_4(z;q)\end{align}
命題7を見ると$$\vartheta_3(2z;q^4)=1+2\sum_{n=1,\mathrm{even}}^\infty q^{n^2}\cos2\pi nz$$$$\vartheta_2(2z;q^4)=2\sum_{n=1,\mathrm{odd}}^\infty q^{n^2}\cos2\pi nz$$となってすぐに示せる。
4つのテータ関数の周期性あるいは擬周期性を確認せよ。次のようになる:\begin{align}\vartheta_1(z+1) &=-\vartheta_1(z)\\\vartheta_1(z+\tau) &=-q^{-1}e^{-2\pi iz}\vartheta_1(z)\\\vartheta_2(z+1) &=-\vartheta_2(z)\\\vartheta_2(z+\tau) &=q^{-1}e^{-2\pi iz}\vartheta_2(z)\\\vartheta_3(z+1) &=\vartheta_3(z)\\\vartheta_3(z+\tau) &=q^{-1}e^{-2\pi iz}\vartheta_3(z)\\\vartheta_4(z+1) &=\vartheta_4(z)\\\vartheta_4(z+\tau) &=-q^{-1}e^{-2\pi iz}\vartheta_4(z)\end{align}
$z+1$ のほうは命題7に代入して三角関数の加法定理等ですぐ得られます。$z+\tau$ のほうは、例えば(10)を用いて\begin{align}\vartheta_1(z+\tau)&=-\vartheta_{11}(z+\tau)\\&=e^{\frac{\pi i}{4}\tau+\pi i(z+\tau+\frac{1}{2})}\;\vartheta\left(z+\tau+\frac{1+\tau}{2}\right)\\&=q^{-1}e^{-2\pi iz}\vartheta_{11}(z)\\&=-q^{-1}e^{-2\pi iz}\vartheta_{1}(z)\end{align}のようにできます。
4つのテータ関数の半周期の変換を確認せよ。次のようになる:\begin{align}\vartheta_1\left(z+\frac{1}{2}\right) &=\vartheta_2(z)\\\vartheta_1\left(z+\frac{\tau}{2}\right) &=iq^{-\frac{1}{4}}e^{-\pi iz}\vartheta_4(z)\\\vartheta_2\left(z+\frac{1}{2}\right) &=-\vartheta_1(z)\\\vartheta_2\left(z+\frac{\tau}{2}\right) &=q^{-\frac{1}{4}}e^{-\pi iz}\vartheta_3(z)\\\vartheta_3\left(z+\frac{1}{2}\right) &=\vartheta_4(z)\\\vartheta_3\left(z+\frac{\tau}{2}\right) &=q^{-\frac{1}{4}}e^{-\pi iz}\vartheta_2(z)\\\vartheta_4\left(z+\frac{1}{2}\right) &=\vartheta_3(z)\\\vartheta_4\left(z+\frac{\tau}{2}\right) &=iq^{-\frac{1}{4}}e^{-\pi iz}\vartheta_1(z)\end{align}
例2と同様です。$z+\frac{1}{2}$ のほうは命題7に代入して三角関数の加法定理等ですぐに得られます。$z+\frac{\tau}{2}$ のほうは(10)を用いて計算できます。
4つのテータ関数 $\vartheta_{k}(z)$ ,$(k=1,2,3,4)$ について次を確認せよ。\begin{align}\frac{\vartheta'_k(z+1)}{\vartheta_k(z+1)} &=\frac{\vartheta'_k(z)}{\vartheta_k(z)}\\\frac{\vartheta'_k(z+\tau)}{\vartheta_k(z+\tau)} &=-2\pi i+\frac{\vartheta'_k(z)}{\vartheta_k(z)}\end{align}
例2の結果を使ってすぐ計算できます。
4つのテータ関数について$$\frac{\partial^2\vartheta_k(z,\tau)}{\partial^2z}=4\pi i\frac{\partial\vartheta_k(z,\tau)}{\partial\tau}$$を示せ。
項別微分可能ですから、命題7等によって普通に計算すればOK。
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。