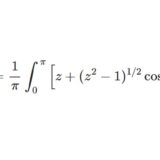記事を大幅に改訂しました(26/1/11)。計算部分は改訂前と変わっていませんが、解説をバージョンアップ。
$\a,\b\in\CC$ とする。$$B(\a,\b)=-\frac{e^{-\pi i(\a+\b)}}{4\sin\pi\a\sin\pi\b}\oint_Pt^{\a-1}(1-t)^{\b-1}dt$$ただし経路 $P$ はポッホハマー積分路であり、$1$ を正方向に回り、$0$ を正方向に回り、$1$ を負方向にまわり、$0$ を負方向に回る周回経路である。実軸の $[0,1]$ に切断を入れる。
よく知られた積分表現
よく知られているベータ関数の表現は次のようなものです。
\begin{equation}B(\a,\b)=\int^1_0t^{\a-1}(1-t)^{\b-1}dt\quad(\mathfrak{R}\a,\mathfrak{R}\b>0)\tag{1}\end{equation}
したがって冒頭の複素積分による表現は、(1)よりも適用範囲が広く、拡張したものとなっています。拡張したというからには、$\mathfrak{R}\a$ , $\mathfrak{R}\b>0$ の範囲で一致するはずです。それを確かめましょう。
そもそもベータ関数ってどういうものなの?という方はこちらをご覧ください:
ガンマ関数とハンケル積分路
本記事の流れは、ガンマ関数のハンケル表示を導出する方法と似ています。ハンケル表示のほうが簡単なので、先に読んでおいてもいいかもしれません:
さて、冒頭の拡張された定義を再掲します。
$\a,\b\in\CC$ とする。$$B(\a,\b)=-\frac{e^{-\pi i(\a+\b)}}{4\sin\pi\a\sin\pi\b}\oint_Pt^{\a-1}(1-t)^{\b-1}dt$$ただし経路 $P$ はポッホハマー積分路であり、$1$ を正方向に回り、$0$ を正方向に回り、$1$ を負方向にまわり、$0$ を負方向に回る周回経路である。実軸の $[0,1]$ に切断を入れる。
この式を見ても、何やら訳が分かりません。どうにかして具体的に計算してみたいです。
そこで次の制限をします。
◎ $\mathfrak{R}\a,\mathfrak{R}\b>0$
◎積分路を実軸ぎりぎりに近づける
このとき$$\oint_Pt^{\a-1}(1-t)^{\b-1}dt$$を計算して、私たちがよく知っている形に落としこむことができます。
経路の設定と偏角の変化
\begin{equation}\oint_Pt^{\a-1}(1-t)^{\b-1}dt\tag{2}\end{equation}なる積分を考えます。ただし積分路は下図。
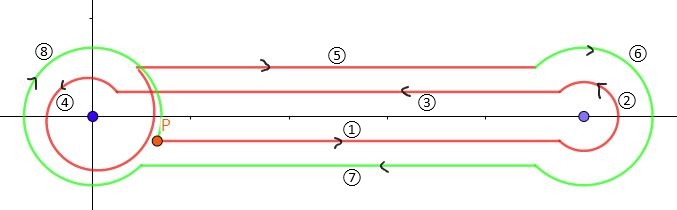
まず原点から実軸に沿って進み、1のまわりで小さな円を正方向に描きます。また実軸に沿って原点にいき、そのまわりで小さな円を正方向に描きます。さらにまた1へ行き、小さな円を負方向に描き、原点へ戻ってまた負方向に円を描いて終わりです。
$t$ と $1-t$ の偏角に注意しながら積分をします。$t=0,1$ が分岐点となっているので、本当は少々の下準備が要るのですが、とりあえず気にせず手順を説明します。
まず、スタート位置Pでは $\arg t=0$ , $\arg(1-t)=0$ とします。2つの偏角を以下のように連続して変化させます。
① Pから1までは $\arg t=\arg(1-t)=0$
② $1$ を回る間、$\arg(1-t)$ は $0$ から $2\pi$ へ変化する。$\arg t=0$ のまま。
③ $0$ へ向かう間、$\arg t=0$ , $\arg(1-t)=2\pi$
④ $0$ を回る間、$\arg t$ は $0$ から $2\pi$ へ変化する。その間 $\arg(1-t)=2\pi$
⑤ $1$ へ向かう間、$\arg t=\arg(1-t)=2\pi$
⑥ $1$ を回る間、 $\arg(1-t)$ は $2\pi$ から $0$ へ変化する。$\arg t=2\pi$ のまま。
⑦ $0$ へ向かう間、$\arg t=2\pi$ , $\arg(1-t)=0$
⑧ $0$ を回る間、$\arg t$ は $2\pi$ から $0$ へ変化する。その間 $\arg(1-t)=0$
変数変換
上記の番号に対応する置換は以下のようになります。$\epsilon>0$ は小さな数とします。
① $t\to t$ , $1-t\to1-t$
② $t\to 1$ (正確には$1-\epsilon e^{i\t}$) , $1-t\to\epsilon e^{i\t}$ , $\t$ は $0\to 2\pi$ と変化
③ $t\to t$ , $1-t\to (1-t)e^{2\pi i}$
④ $t\to\epsilon e^{i\t}$ , $1-t\to e^{2\pi i}$ , $\t$ は $0\to 2\pi$ と変化
⑤ $t\to te^{2\pi i}$ , $1-t\to(1-t)e^{2\pi i}$
⑥ $t\to e^{2\pi i}$ , $1-t\to\epsilon e^{i\t}$ , $\t$ は $2\pi\to 0$ と変化
⑦ $t\to te^{2\pi i}$ , $1-t\to 1-t$
⑧ $t\to\epsilon e^{i\t}$ , $1-t\to 1$ , $\t$ は $2\pi\to 0$ と変化
補足します。⑤で $t$ を $te^{2\pi i}$ と書き換えています。これは $t$ の偏角が $2\pi i$ であることを示しています。パッと見て無意味な変換のようですが、$t^{\a-1}$ と $(te^{2\pi i})^{\a-1}$ は一般に異なる値になるのです(試しに $\a=1/2$ としてみてください)。
④の経路は $t=0$ まわりの小円なので $1-t=1$ なのですが、$\arg(1-t)=2\pi i$ なので $1-t=e^{2\pi i}$ となります。
このように経路をとると、⑧の最後は $\arg t=0$ , $\arg(1-t)=0$ となって、スタート位置の偏角に戻っています。よってこの積分路において被積分関数は連続して変化し、最終的にピタリと一周できているということになります。
積分経路の補足
経路を再掲します。

例えば①と⑤はまったく同じ道筋なのに、上記の変換のために積分値は異なります。これは本来の複素積分の状況からすると変です。しかもいくつもの箇所で交わったりしています。
ここにはカラクリがあります。気にならない方は読み飛ばしてそのまま計算しちゃってください。
この積分では $t=0,1$ が分岐点になっています。よって $0$ と $1$ の間に実軸に沿って切断(cut)を入れ、新たなリーマン面を導入します。$0$ を1周する、または $1$ を1周すると「別世界」へ行くのです。
まず①はもともとの世界 $\Sigma_{1,1}$。②で $1$ のまわりを1周した直後には別の世界 $\Sigma_{1,2}$ に移ります。なので③は $\Sigma_{1,2}$ の世界です。冒頭の経路で①と③は同じところを走る直線に見えますが、これらは世界が違うのです!$\Sigma_{1,2}$ の世界では「$1-t$ の偏角が $2\pi$ 増加する」。だから上のような変換を受け、積分値も異なります。
次に④で $0$ まわりをまわった直後に $\Sigma_{2,2}$ という世界に入ります。$\Sigma_{2,2}$ は「$t$ および $1-t$ の偏角が $2\pi$ 増加する」世界です。なので⑤も $\Sigma_{2,2}$ の世界での直線で、①や③と異なります。
⑥では $1$ を逆回りします。すると $\Sigma_{2,1}$ という世界になり、「$t$ の偏角が $2\pi$ 増加する」。⑦の直線もこの世界のものです。
最後に⑧で $0$ を逆回りすると、元の世界 $\Sigma_{1,1}$ に戻ります。
このように考えると、実は積分路は一度も交わっていないのです。世界が違うので。
一般化すると、もとの世界から $0$ を $m$ 周、 $1$ を $n$ 周すると $\Sigma_{m+1,n+1}$ なる世界に移り、$t$ の偏角は $+2\pi im$ , $1-t$ の偏角は $+2\pi in$ されます。逆回りすると $m,n$ の値は減ります。
円弧の積分
②の経路に関しては\begin{eqnarray*}\left|\int_0^{2\pi}(1-\epsilon e^{i\t})^{\a-1}(\epsilon e^{i\t})^{\b-1}(-i\epsilon e^{i\t})d\t\right|&\le&\epsilon^{\mathfrak{R}\b}\int_0^{2\pi}\left|(1-\epsilon e^{i\t})^{\a-1}\right|d\t\\&&\xrightarrow[\epsilon\to0]{}0\end{eqnarray*}④⑥⑧も同様です。$\mathfrak{R}\a,\mathfrak{R}\b>0$ を仮定していたのを利用しています。
あとは①③⑤⑦を考えればいいですね。\begin{eqnarray*}&&\oint_Pt^{\a-1}(1-t)^{\b-1}dt\\&=&\int_0^1t^{\a-1}(1-t)^{\b-1}dt+\int_1^0t^{\a-1}\left((1-t)e^{2\pi i}\right)^{\b-1}dt\\&&+\int_0^1\left(te^{2\pi i}\right)^{\a-1}\left((1-t)e^{2\pi i}\right)^{\b-1}dt+\int_1^0\left(te^{2\pi i}\right)^{\a-1}(1-t)^{\b-1}dt\\&=&\int_0^1t^{\a-1}(1-t)^{\b-1}dt-\int_0^1t^{\a-1}(1-t)^{\b-1}e^{2\pi i\b}dt\\&&+\int_0^1t^{\a-1}e^{2\pi i\a}(1-t)^{\b-1}e^{2\pi i\b}dt-\int_0^1t^{\a-1}e^{2\pi i\a}(1-t)^{\b-1}dt\\&=&(e^{2\pi i\a}-1)(e^{2\pi i\b}-1)\int_0^1t^{\a-1}(1-t)^{\b-1}dt\\&=&e^{\pi i(\a+\b)}(e^{\pi i\a}-e^{-\pi i\a})(e^{\pi i\b}-e^{-\pi i\b})\int_0^1t^{\a-1}(1-t)^{\b-1}dt\\&=&-4e^{\pi i(\a+\b)}\sin\pi\a\sin\pi\b \int_0^1t^{\a-1}(1-t)^{\b-1}dt\end{eqnarray*}最後に現れたのはよく知られたベータ関数の積分表示です。
以上から次の結論を得ます。
ポッホハマーによるベータ関数の表示$$B(\a,\b)=-\frac{e^{-\pi i(\a+\b)}}{4\sin\pi\a\sin\pi\b}\oint_Pt^{\a-1}(1-t)^{\b-1}dt$$は $\mathfrak{R}\a,\mathfrak{R}\b>0$ においては$$\int_0^1t^{\a-1}(1-t)^{\b-1}dt$$に一致する。
$\a,\b\in\ZZ$ では先ほどの途中式$$\oint_Pt^{\a-1}(1-t)^{\b-1}dt=(e^{2\pi i\a}-1)(e^{2\pi i\b}-1)B(\a,\b)$$を見ると右辺は明らかに $0$。左辺の積分は $\a,\b\in\ZZ$ では先ほどの偏角の操作は不要で、積分路は完全に相殺されて値 $0$ となります。
Whittaker-Watsonを参考にして導出しました。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。