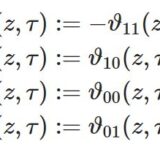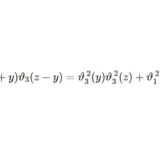前回は:
テータ関数は整関数なので極はありません。
なので零点に関する議論をしましょう。4つのテータ関数 $\vartheta_1(z)$,$\vartheta_2(z)$,$\vartheta_3(z)$,$\vartheta_4(z)$ のどれでもいいので $\vartheta_k(z)$ と書いておきます。前回の例題より周期性あるいは擬周期性:\begin{align}\vartheta_1(z+1) &=-\vartheta_1(z)\tag{0a}\\\vartheta_1(z+\tau) &=-q^{-1}e^{-2\pi iz}\vartheta_1(z)\tag{0b}\\\vartheta_2(z+1) &=-\vartheta_2(z)\tag{0c}\\\vartheta_2(z+\tau) &=q^{-1}e^{-2\pi iz}\vartheta_2(z)\tag{0d}\\\vartheta_3(z+1) &=\vartheta_3(z)\tag{0e}\\\vartheta_3(z+\tau) &=q^{-1}e^{-2\pi iz}\vartheta_3(z)\tag{0f}\\\vartheta_4(z+1) &=\vartheta_4(z)\tag{0g}\\\vartheta_4(z+\tau) &=-q^{-1}e^{-2\pi iz}\vartheta_4(z)\tag{0h}\end{align}が分かっています。これより任意の整数 $m,n$ に対して\begin{equation}\vartheta_k(z+m\tau+n)=\Box\cdot\vartheta_k(z)\tag{1}\end{equation}の形になることが分かります。ただし $\Box$ は零点を持たない $z$ の関数です。いま $\vartheta_k(z)$ の零点を $z=z_0$ とすると、(1)より $z_0+m\tau+n$ も零点になっています。$$\vartheta_k(z_0)=0\Longrightarrow \vartheta_k(z_0+m\tau +n)=0$$
テータ関数は楕円関数でないので二重周期をもつわけではありませんが、零点に関していうと「二重周期性」があり、2つの周期 $1,\tau$ がつくる基本平行四辺形ごとに $z_0$ と合同な零点があるということです。
楕円関数のときと同様、複素平面に敷き詰められた基本平行四辺形は丸ごと適当に平行移動して考えることができます。テータ関数に零点がいくつあるかはまだ判明していませんが、零点は平行四辺形ごとに有限個ですので、零点が平行四辺形の境界上に来ないように基本平行四辺形を移動しておきましょう。この基本平行四辺形1つ1つをセルとよびます。
いま、セル $C$ を考えます。$C$ は $a$,$a+1$,$a+1+\tau$,$a+\tau$ の4点からなる平行四辺形です。この内部に零点 $z_0$ があれば、他のすべてのセルにも対応する零点があります($z_0$ と合同な点)。
さて、1つのセル内に零点はいくつあるでしょう?
零点の数を調べるには偏角の原理がよいです。偏角の原理では閉曲線内にある零点と極の個数差を求めることができますが、テータ関数には極が無いので、偏角の原理によってまさに零点の個数が現れるのです。 $C$ 内にある零点の個数を $N$ とすると\begin{align}N&=\frac{1}{2\pi i}\oint_C\frac{\vartheta'_k(z)}{\vartheta(z)}dz\\&=\frac{1}{2\pi i}\left[\int_a^{a+1}+\int_{a+1}^{a+1+\tau}+\int_{a+1+\tau}^{a+\tau}+\int_{a+\tau}^a\right]\\&=\frac{1}{2\pi i}\left[\int_a^{a+1}\frac{\vartheta'_k(z)}{\vartheta(z)}dz+\int_{a}^{a+\tau}\frac{\vartheta'_k(z+1)}{\vartheta(z+1)}dz+\int_{a+1}^{a}\frac{\vartheta'_k(z+\tau)}{\vartheta(z+\tau)}dz+\int_{a+\tau}^a\frac{\vartheta'_k(z)}{\vartheta(z)}dz\right]\end{align}前回の例題から\begin{align}\frac{\vartheta'_k(z+1)}{\vartheta_k(z+1)} &=\frac{\vartheta'_k(z)}{\vartheta_k(z)}\tag{2}\\\frac{\vartheta'_k(z+\tau)}{\vartheta_k(z+\tau)} &=-2\pi i+\frac{\vartheta'_k(z)}{\vartheta_k(z)}\tag{3}\end{align}でしたので$$\therefore\quad N=1$$これで零点の個数が分かりました。
4つのテータ関数 $\vartheta_1(z)$,$\vartheta_2(z)$,$\vartheta_3(z)$,$\vartheta_4(z)$ はいずれもセル内に1位の零点を1つもつ。極はもたない。
テータ関数の零点は(セルごとに)1つと分かりました。それはどこでしょうか。
とても簡単な話です。前回の命題7より\begin{align}\vartheta_1(z) &=2\sum_{n=0}^{\infty}(-1)^n q^{(n+\frac{1}{2})^2}\sin(2n+1)\pi z\tag{4}\\\vartheta_2(z) &=2\sum_{n=0}^{\infty} q^{(n+\frac{1}{2})^2}\cos(2n+1)\pi z\tag{5}\\\vartheta_3(z) &= 1+2\sum_{n=1}^\infty q^{n^2}\cos2\pi nz\tag{6}\\\vartheta_4(z) &= 1+2\sum_{n=1}^\infty (-1)^nq^{n^2}\cos2\pi nz\tag{7}\end{align}ですが、(4)より\begin{equation}\vartheta_1(0)=0\tag{8}\end{equation}は明らかです。同じく前回の例題で得た式:\begin{align}\vartheta_1\left(z+\frac{1}{2}\right) &=\vartheta_2(z)\tag{9}\\\vartheta_1\left(z+\frac{\tau}{2}\right) &=iq^{-\frac{1}{4}}e^{-\pi iz}\vartheta_4(z)\tag{10}\\\vartheta_2\left(z+\frac{1}{2}\right) &=-\vartheta_1(z)\tag{11}\\\vartheta_2\left(z+\frac{\tau}{2}\right) &=q^{-\frac{1}{4}}e^{-\pi iz}\vartheta_3(z)\tag{12}\\\vartheta_3\left(z+\frac{1}{2}\right) &=\vartheta_4(z)\tag{13}\\\vartheta_3\left(z+\frac{\tau}{2}\right) &=q^{-\frac{1}{4}}e^{-\pi iz}\vartheta_2(z)\tag{14}\\\vartheta_4\left(z+\frac{1}{2}\right) &=\vartheta_3(z)\tag{15}\\\vartheta_4\left(z+\frac{\tau}{2}\right) &=iq^{-\frac{1}{4}}e^{-\pi iz}\vartheta_1(z)\tag{16}\end{align}を活用すれば\begin{align}\vartheta_2\left(\frac{1}{2}\right)&=0\tag{17}\\\vartheta_3\left(\frac{1+\tau}{2}\right)&=0\tag{18}\\\vartheta_4\left(\frac{\tau}{2}\right)&=0\tag{19}\end{align}(8)(17)(18)(19)を見ると、$\vartheta_1(z)$,$\vartheta_2(z)$,$\vartheta_3(z)$,$\vartheta_4(z)$ の零点は $0$,$1/2$,$(1+\tau)/2$,$\tau/2$ でできる平行四辺形の頂点を反時計回りにみて割り当てられていることが分かります。添え字の順番は零点の頂点の順番に由来するのでしょうか??
4つのテータ関数 $\vartheta_1(z)$,$\vartheta_2(z)$,$\vartheta_3(z)$,$\vartheta_4(z)$ はそれぞれ$$0\;,\;\frac{1}{2}\;,\;\frac{1+\tau}{2}\;,\;\frac{\tau}{2}$$を1位の零点としてもつ。これ(と合同な点)以外に零点はもたない。
この零点はペー関数の導関数 $\wp'(z)$ のものと似ているなぁと思いました。
(9)(11)を見ると2つのテータ関数の関係は $\sin\pi x$ , $\cos\pi x$ の間の関係みたいに見えませんか?サインとコサインは2乗したものどうしを足すと1になります。テータ関数にもそんな感じの関係式ができないものか。
そこでテータ関数の2乗を考えます。$\vartheta_k(z)^2$ は整関数で2位の零点を1つもつのみです。よってその逆数$$\frac{1}{\vartheta_k(z)^2}$$は2位の極をもちます。さらに $j\neq k$ として$$X_{jk}(z):=\frac{\vartheta_j(z)^2}{\vartheta_k(z)^2}$$をつくります。これは2位の極と2位の零点をもちます。しかも式(0)を使うと$$\frac{\vartheta_j(z+1)^2}{\vartheta_k(z+1)^2}=\frac{\vartheta_j(z+\tau)^2}{\vartheta_k(z+\tau)^2}=\frac{\vartheta_j(z)^2}{\vartheta_k(z)^2}$$であることが確かめられ、$X_{jk}(z)$ は二重周期をもつ楕円関数であることが判明します。
過去記事でも散々あったように、複数の楕円関数の間で成り立つ関係式を求めるために極や零点の個数を考えることはよくあります。次の関数を考えましょう。$$F(z)=\frac{a\vartheta_1(z)^2+b\vartheta_4(z)^2}{\vartheta_2(z)^2}$$$a,b$ は $z$ によらない定数です。この $F(z)$ は二重周期をもつので楕円関数であり、分母のために $z=1/2$ に2位の極をもっています。そこで定数 $a,b$ を適切に決めて $z=1/2$ が分子の零点になるようにします。すなわち\begin{equation}F(z):=\frac{\left(\frac{\vartheta_1(z)}{\vartheta_1(1/2)}\right)^2-\left(\frac{\vartheta_4(z)}{\vartheta_4(1/2)}\right)^2}{\vartheta_2(z)^2}\tag{20}\end{equation}とするのです。すると $F(z)$ 全体としては2位の極 $z=1/2$ が分子で相殺されるので、結局 1位の極を1個あるいは0個もつことになります。このような楕円関数は定数に限ることから $F(z)$ は定数関数です。よって$$A\vartheta_2(z)^2=\left(\frac{\vartheta_1(z)}{\vartheta_1(1/2)}\right)^2-\left(\frac{\vartheta_4(z)}{\vartheta_4(1/2)}\right)^2$$$\vartheta_1(1/2)=\vartheta_2(0)$ です。テータ関数において $z=0$ の値はテータ定数とよび、簡単のために $\vartheta_2(0)=\vartheta_2$ のように書きます。すると$$A\vartheta_2(z)^2=\left(\frac{\vartheta_1(z)}{\vartheta_2}\right)^2-\left(\frac{\vartheta_4(z)}{\vartheta_3}\right)^2$$です。$z=0$ を代入すれば $A$ が求まります。結局\begin{equation}\vartheta_4^{~2}\vartheta_2(z)^2=\vartheta_2^{~2}\vartheta_4(z)^2-\vartheta_3^{~2}\vartheta_1(z)^2\tag{21}\end{equation}テータの記号が多すぎて戸惑いますが、(21)は単に $\vartheta_1(z)$,$\vartheta_2(z)$,$\vartheta_4(z)$ の関係式(以下"1,2,4の関係"と呼ぼう)であってほかは定数であるという整理をしましょう。 定数 $\vartheta_2$ などの値を明示的に書ければよいのですが、$\tau$ の値にもよりますし、いずれにしてもそう簡単ではありません。
全く同様に\begin{equation}G(z):=\frac{\left(\frac{\vartheta_1(z)}{\vartheta_1((1+\tau)/2)}\right)^2-\left(\frac{\vartheta_4(z)}{\vartheta_4((1+\tau)/2)}\right)^2}{\vartheta_3(z)^2}\tag{22}\end{equation}を用いると\begin{equation}\vartheta_4^{~2}\vartheta_3(z)^2=\vartheta_3^{~2}\vartheta_4(z)^2-\vartheta_2^{~2}\vartheta_1(z)^2\tag{23}\end{equation}これは1,3,4の関係式です。(21)(23)の $z$ に $z+1/2$ を代入すると残り2つの関係式が出てきます。
\begin{align}\vartheta_4^{~2}\vartheta_2(z)^2&=\vartheta_2^{~2}\vartheta_4(z)^2-\vartheta_3^{~2}\vartheta_1(z)^2\\\vartheta_4^{~2}\vartheta_3(z)^2&=\vartheta_3^{~2}\vartheta_4(z)^2-\vartheta_2^{~2}\vartheta_1(z)^2\\\vartheta_4^{~2}\vartheta_1(z)^2&=\vartheta_2^{~2}\vartheta_3(z)^2-\vartheta_3^{~2}\vartheta_2(z)^2\\\vartheta_4^{~2}\vartheta_4(z)^2&=\vartheta_3^{~2}\vartheta_3(z)^2-\vartheta_2^{~2}\vartheta_2(z)^2\end{align}
定理3の4つめの式で $z=0$ とすると次の系を得ます。
$$\vartheta_2^{~4}+\vartheta_4^{~4}=\vartheta_3^{~4}$$
(22)を用いて(23)を導け。
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

つぎはこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。