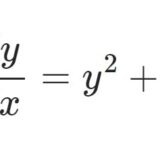前回:
非線型微分方程式を解くのはもちろん難しい。ここでは逆に、解から方程式をつくり、非線型方程式の現れ方に馴染んでみよう。その形がいかに予測困難かを実感することも含めて。
例えば $y'=x$ なる1階線型方程式の解は $y=x^2/2+c$ です。1階の方程式なので任意定数が1つ含まれます。
逆に $y=x^2/2+c$ が与えられたとします。これはおなじみの放物線で、パラメータ $c$ を含んでいます。これを一般解とする微分方程式をどのようにしてつくるか。単純な話、微分すればよいわけです。
微分方程式を解くのはそれなりのテクニックや熟練を要しますが、逆に解から微分方程式をつくるのは比較的容易ということが分かります。
もし2階の方程式をつくりたかったらどうでしょう。解は任意定数を2つもつことになります。例として\begin{equation}y=ax^2+ax+b\tag{1}\end{equation}を一般解とする方程式を導出します。2回微分すると \begin{align}y'&=2ax+a\tag{2}\\y''&=2a\tag{3}\end{align}(2)(3)から $a$ を消すと\begin{equation}y'=\left(x+\frac{1}{2}\right)y''\tag{4}\end{equation}となり、2階線型微分方程式が完成しました。導出のキモは任意定数となるパラメータを消すことにあります。
一般的な話をしましょう。いま、パラメータ $\a$ , $\b$ を含む曲線\begin{equation}f(x,y,\a,\b)=0\tag{5}\end{equation}があるとします(1階をつくりたければ $\b$ は不要)。$x$ で微分します。$y$ は $x$ の関数なのでチェインルールを使います。\begin{equation}\dd{f}{x}+\dd{f}{y}\frac{dy}{dx}=0\tag{6}\end{equation}(6)を再度微分して\begin{align}\left\{\frac{\partial^2f}{\partial x^2}+\frac{\partial}{\partial y}\left(\dd{f}{x}\right)\cdot\frac{dy}{dx}\right\}+\left\{\dd{f}{y}\frac{d^2y}{dx^2}+\left(\frac{\partial^2f}{\partial y\partial x}+\frac{\partial^2f}{\partial y^2}\frac{dy}{dx}\right)\frac{dy}{dx}\right\}=0\end{align}\begin{equation}\therefore\quad \frac{\partial^2 f}{\partial x^2}+2\frac{\partial^2f}{\partial x\partial y}\frac{dy}{dx}+\dd{f}{y}\frac{d^2y}{dx^2}+\frac{\partial^2 f}{\partial y^2}\left(\frac{dy}{dx}\right)^2=0\tag{7}\end{equation}(5)(6)(7)から $\a$ , $\b$ を消すと、目標である2階の微分方程式を得ます。
実際に非線型方程式をつくってみましょう。
曲線\begin{equation}(x-a)^2+(y-b)^2=R^2\tag{8}\end{equation}ただしパラメータは $a$, $b$ である。
微分すると\begin{align}x-a+(y-b)y'=0\tag{9}\\(y-b)y''+1+y'^2=0\tag{10}\end{align}(9)を $x-a$ について解いて(8)に代入すると$$(y-b)^2(1+y'^2)=R^2$$これに、(9)を $y-b$ について解いたものを代入すれば\begin{equation}R^2y''^2=(1+y'^2)^3\tag{11}\end{equation}これが求める方程式である。
例1は半径が $R$ で中心の位置が $xy$ 平面上で任意の円です。(11)は $x,y$ を含まず $F(y'',y')=0$ の形をしていますので過去記事の知見で解くことができます。でも(11)をぱっと見せられて、これが円だとはなかなか分からないのも面白いです。なお(11)は一般解(8)では表せない特異解 $x^2+y^2=0$ をもちます。
曲線\begin{equation}y=A e^{Bx^2}\tag{12}\end{equation}
微分すると$$y'=2Bxy$$再度微分すると$$y''=2By+2Bxy'=\frac{y'}{x}+\frac{y'^2}{y}$$したがって(12)を一般解とする方程式は\begin{equation}xyy''=yy'+xy'^2\tag{13}\end{equation}
(12)の係数 $A$ は線型方程式でもよく見られますが、$B$ は線型の議論では見たことがありません。このように変な(?)ところに任意定数がつくのも非線型微分方程式の特徴です。
曲線\begin{equation}2y^2\ln(cy)=x^2\tag{14}\end{equation}
パラメータは1つなので1階微分で十分である。実際微分すると$$2\ln(cy)=\frac{x}{yy'}-1$$を得る。これを(14)に代入して\begin{equation}(x^2+y^2)y'=xy\tag{15}\end{equation}が求める方程式である。
$b,h$ をパラメータとする2次曲線$$x^2+2hxy+by^2=K$$
答えは [1] にあって$$Ky^2y''+Ky'^2(xy'-y)+(y-xy')^3=0$$
関数 $a(x),b(x),c(x),d(x)$ およびパラメータ $k$ を含む曲線\begin{equation}y=\frac{a(x)+k\:b(x)}{c(x)+k\:d(x)}\tag{16}\end{equation}
(16)より\begin{equation}k=\frac{cy-a}{b-dy}\tag{17}\end{equation}(16)を微分して$$y'=\frac{a'+kb'}{c+kd}-y\frac{c'+kd'}{c+kd}$$分母を払って $k$ について解くと\begin{equation}k=\frac{a'-cy'-c'y}{dy'+d'y-b'}\tag{18}\end{equation}(17)=(18)なので$$(cy-a)(dy'+d'y-b')=(b-dy)(a'-cy'-c'y)$$展開して整理すると$$(bc-ad)y'+(a'd-ad'+bc'-b'c)y+(cd'-c'd)y^2=a'b-ab'$$$bc-ad\equiv 0$ なら $y$ の関数形がただちに完成する。$bc-ad\not\equiv 0$ とすると\begin{equation}y'+P(x)y+Q(x)y^2=R(x)\tag{19}\end{equation}の形となる(Riccati型微分方程式)。
例5の具体的な形として、次をやってみましょう。
曲線\begin{equation}y=\frac{1+kx}{x+2kx^2}\tag{20}\end{equation}
例5と全く同様の手順である。$k$ について解くと\begin{equation}k=\frac{1-xy}{2x^2y-x}\tag{21}\end{equation}(20)を微分すると$$y'=\frac{k}{x+2kx^2}-y\frac{1+4kx}{x+2kx^2}$$\begin{equation}\therefore\quad k=\frac{-xy'-y}{2x^2y'+4xy-1}\tag{22}\end{equation}(21)=(22)より\begin{equation}y'+\frac{4}{x}y-2y^2=\frac{1}{x^2}\tag{23}\end{equation}と求まる。
うまくパラメータを消すテクニックがあると早くできます。次の例はどうでしょう。
パラメータ $a,b$ を含む曲線\begin{equation}y=\frac{1}{x-a}+\frac{1}{x-b}\tag{24}\end{equation}
$\frac{1}{x-a}$ , $\frac{1}{x-b}$ をそれぞれまとまりとみて、対称性に注目。微分して$$-y'=\frac{1}{(x-a)^2}+\frac{1}{(x-b)^2}$$これと(24)から\begin{equation}\frac{1}{x-a}\frac{1}{x-b}=\frac{y^2+y'}{2}\tag{25}\end{equation}(24)(25)は $\frac{1}{x-a}$ , $\frac{1}{x-b}$ の基本対称式である。(24)の2階微分は$$\frac{y''}{2}=\frac{1}{(x-a)^3}+\frac{1}{(x-b)^3}$$右辺は基本対称式で書くことができるので(24)(25)を用いて\begin{equation}y''+3yy'+y^3=0\tag{26}\end{equation}
曲線\begin{equation}(y+a)^3=(x+b)^2\tag{27}\end{equation}
微分すると\begin{equation}3y'=2(x+b)^{-1/3}\tag{28}\end{equation}再度微分して$$y''=-\frac{2}{9}(x+b)^{-4/3}$$これに(28)を $x+b$ について解いたものを代入すると\begin{equation}8y''+9y'^4=0\tag{29}\end{equation}
(29)も $x,y$ を含まず $F(y'',y)=0$ の形をしています。$u=y'$ と置けばすれば、変数分離によって容易に(27)を導けます。
[1] H.T.Davis (1960), Introduction to nonlinear differential and integral equations, U.S. Atomic Energy Commission
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。