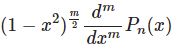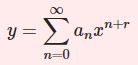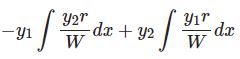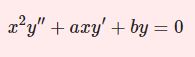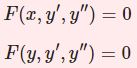線型微分方程式に無限級数を代入して解を求める.
・ふつうの級数法$$y=\sum_{n=0}^\infty a_nx^n$$
・フロベニウス法$$y=\sum_{n=0}^\infty a_nx^{n+r} \quad,\quad(a_0\neq 0)$$
たとえば2階線型微分方程式$$y^{\prime\prime}+p(x)y'+q(x)y=0$$の形になっているときに $x=0$ で特異点をもたない場合はふつうの級数法(以下「級数法」)、特異点をもつ場合はフロベニウス法を使います。
※ $x=0$ 以外の点で特異点をもつかを考えることもあります。ただ、本シリーズでは原則として $x=0$ まわりの展開を考えます。細かいことをいえば、特異点のなかでも確定特異点と不確定特異点があり、解法が異なることがあります。ここでは気にしない。
微分方程式と特異点については
などできちんと論じています。
今回の解法は面倒なのであくまで最終手段です。
もたなければ級数法$$例\quad y^{\prime\prime}+xy'-y=0$$
もてばフロベニウス法$$例\quad y^{\prime\prime}+\frac{1}{x}y'-y=0$$
係数を比較して漸化式を解いたり。
ただしフロベニウス法ではまず決定方程式を解いてから。
無限級数の正体が実は身近な関数だったりします
2階線型微分方程式なら$$y^{\prime\prime}+p(x)y'+q(x)y=0$$に$$y=\sum_{n=0}^\infty a_nx^n$$ を代入して ${a_n}$ を求めることで解を無限級数の形であらわします。この級数は $y$ を $x=0$ のまわりで展開した形になっていますが、微分方程式が $x=0$ で特異点を持っている場合、この方法は通用しません。$y''$ に何も係数がついていない形にしたときの $y',y$ の係数が $p(x),q(x)$ ですが、これらが例えば $1/x$ のような形の場合は $x=0$ で分母ゼロになるため特異点であり、別の方法が必要になります。
まずは微分方程式が $x=0$ で特異点を持たないケースを紹介します。
$y'-y=0$ を解け.
$x=0$ は特異点でないので級数法を用います。まぁ級数法を使わずとも簡単に求まるでしょうが・・・。$$y=\sum_{n=0}^\infty a_nx^n$$とおけば$$y'=\sum^\infty_{n=1}na_{n}x^{n-1}=\sum^\infty_{n=0}(n+1)a_{n+1}x^{n}$$これらを方程式に代入して\begin{eqnarray*}&&y'-y=0\\\Leftrightarrow &&\sum^\infty_{n=0}(n+1)a_{n+1}x^{n}-\sum_{n=0}^\infty a_nx^n=0\\\Leftrightarrow &&\sum^\infty_{n=0}[(n+1)a_{n+1}-a_n]x^n=0\end{eqnarray*}最後に得られた左辺が恒等的に$0$なので $1,x,x^2,x^3,\cdots$ の項の係数がすべて $0$ です。
$$\therefore\quad a_{n+1}=\frac{a_n}{n+1}\quad(n\ge 0)$$典型的な漸化式であり、一般項は$$a_n=\frac{1}{n!}a_0\quad(n\ge 0)$$
さて、そもそも$$y=\sum_{n=0}^\infty a_nx^n$$ですから求まった $a_n$ を代入すると\begin{eqnarray*}y&=&\sum_{n=0}^\infty\frac{1}{n!}a_0x^n\\&=&a_0e^x\end{eqnarray*}と一般解が求まりました。最後の等号では、求まった無限級数が既知の関数 $e^x$ と一致していることに気づいたものです。1階線型微分方程式ですので、不定の定数が1つあります。
$y^{\prime\prime}-4xy'+(4x^2-2)y=0$ を解け.
$x=0$ で特異点でないので級数法を用います。$$y=\sum_{n=0}^\infty a_nx^n$$とおけば$$y'=\sum^\infty_{n=1}na_{n}x^{n-1}$$$$y^{\prime\prime}=\sum^\infty_{n=2}n(n-1)a_{n}x^{n-2}=\sum^\infty_{n=0}(n+2)(n+1)a_{n+2}x^n$$これらを微分方程式に代入すると\begin{eqnarray*}&&\sum_{n=0}^\infty(n+2)(n+1)a_{n+2}x^{n}-\sum^\infty_{n=1}4na_{n}x^{n}+\sum_{n=0}^\infty 4a_nx^{n+2}-\sum_{n=0}^\infty 2a_nx^n=0\\\Leftrightarrow &&\sum_{n=0}^\infty {(n+2)(n+1)a_{n+2}-2a_n}x^n-\sum^\infty_{n=1}4na_{n}x^{n}+\sum^\infty_{n=2}4a_{n-2}x^n=0\\\Leftrightarrow&&(2a_2-2a_0)+(6a_3-6a_1)x+\sum^\infty_{n=2}[(n+2)(n+1)a_{n+2}-(4n+2)a_n+4a_{n-2}]x^n=0\end{eqnarray*}最後に得られた左辺の $1,x,x^2,x^3,\cdots$ の項の係数がすべて $0$ でなければならないので$$\begin{cases}a_0 &=&a_2 \\a_1 &=&a_3 \\a_{n+2} &=& 2\displaystyle\frac{(2n+1)a_n-2a_{n-2}}{(n+2)(n+1)} \;\;\;(n\geq 2)\end{cases}$$という数列 ${a_n}$ の漸化式となります。がんばって計算すると$$\begin{cases}a_2 &=& a_0\\a_3 &=& a_1\\a_4&=&\displaystyle\frac{1}{2}a_0\\a_5&=&\displaystyle\frac{1}{2}a_1\\a_6&=&\displaystyle\frac{1}{6}a_0\\a_7&=&\displaystyle\frac{1}{6}a_1\\a_8&=&\displaystyle\frac{1}{24}a_0\end{cases}$$これにより$a_{2m}=\displaystyle\frac{a_0}{m!}\quad(m\ge 0)$ および $a_{2m+1}=\displaystyle\frac{a_1}{m!}\quad(m\ge 0)$ と予想できます。
予想が正しいとすると\begin{eqnarray*}a_{2m+2}&=&2\displaystyle\frac{(4m+1)a_{2m}-2a_{2m-2}}{(2m+2)(2m+1)}\\&=& 2\displaystyle\frac{(4m+1)\frac{a_0}{m!}-2\frac{a_0}{(m-1)!}}{(2m+2)(2m+1)}\\&=& \displaystyle\frac{(4m+1)\frac{1}{m!}-2\frac{1}{(m-1)!}}{(m+1)(2m+1)}a_0\\&=& \displaystyle\frac{(4m+1)-2m}{m!(m+1)(2m+1)}a_0\\&=&\frac{a_0}{(m+1)!}\end{eqnarray*}数学的帰納法により上記の予想は正しいことが分かりました。$a_{2m+3}$ についても同様です。
さてそもそも$$y=\sum_{n=0}^\infty a_nx^n$$ですから求まった $a_n$ を代入すると、偶奇分けて\begin{eqnarray*}y&=&a_0\sum_{m=0}^\infty\frac{1}{m!}x^{2m}+a_1\sum_{m=0}^\infty\frac{1}{m!}x^{2m+1}\\&=&a_0\sum_{m=0}^\infty\frac{1}{m!}(x^2)^m+a_1x\sum_{m=0}^\infty\frac{1}{m!}(x^2)^m\\&=& a_0e^{x^2}+a_1xe^{x^2}\end{eqnarray*}と一般解が求まります。最後に既知の関数と一致することを見抜くことが大切です。
2階線型微分方程式ですので、一般解は2つの解基底の線型結合で表されるはずです。求まった一般解を見ると確かにそういう形になっていますね。
方程式が $x=0$ で特異点をもつ場合です。フロベニウス法では解となる無限級数を以下のように置きます。$$y=\sum_{n=0}^\infty a_nx^{n+r} \quad,\quad(a_0\neq 0)$$$a_0$ が定数項ではなく $x^r$ となっています。$r$ は整数とは限りません。
フロベニウス法の流れとしては、まず無限級数を微分方程式に代入して式を整理します。級数法と同様に恒等式を得ますので $r$ を決定し数列 ${a_n}$ を求めます。2階微分方程式なので $r$ の2次方程式が現れ、一般に $r$ は2つの値をとります。 $r$ を求める2次方程式を「決定方程式」といいます。
2つの $r$ に対してそれぞれ特殊解を得ればその線型結合で一般解が完成します。ただ、のちに見るように $r$ が重解の場合と $r$ が異なる2解を持っても特殊解が独立でない場合には階数低減法などによって別の特殊解を探す必要があります。そういう意味で、前節の級数法よりパターンが多くて複雑といえます。
$x(x-1)y^{\prime\prime}+(3x-1)y'+y=0$ を解け.
この微分方程式は $x(x-1)$ で割ったときに $x=0$ で解析的ではありません。なのでフロベニウス法を使います。$$y=\sum^\infty_{n=0}a_nx^{n+r} \; \; , \; a_0\ne 0$$方程式にこの級数を代入すると$$\sum^\infty_{n=0}[(n+r)(n+r+2)+1]a_nx^{n+r}-\sum^\infty_{n=0}(n+r)^2a_nx^{n+r-1}=0$$
この段階では $r$ は非整数として取り扱ってください。例えば $r=1$ だと仮定すると本来2階微分で $a_0$ の項は消えてしまいます。のちの決定方程式を導くためにも、微分しても項は消えないものとして進めます。
さて最低次の項 $r^2a_0x^{r-1}$ について、$a_0\ne 0$ であることから$$r^2=0$$$r$ を決めるこの式を決定方程式といいます。ここでは重解 $r=0$ のみです。これにより級数の形は$$y=\sum^\infty_{n=0}a_nx^n \; \; , \; a_0\ne 0$$であらわされることが分かります。
あらためて級数を微分方程式に代入すると$$\sum^\infty_{n=2}n(n-1)a_nx^n+\sum^\infty_{n=1}3na_nx^n+\sum^\infty_{n=0}a_nx^n-\sum^\infty_{n=1}n(n+1)a_{n+1}x^n-\sum^\infty_{n=0}(n+1)a_{n+1}x^n=0$$昇べきにまとめると$$(a_0-a_1)+4(a_1-a_2)x+\sum^\infty_{n=2}(n+1)^2(a_n-a_{n+1})x^n=0$$
各項の係数を比較して$$\begin{cases}a_0=a_1 \\a_1=a_2 \\a_n=a_{n+1}\;\; (n\geq 2)\end{cases}$$を得ます。したがってすべての $n$ について $a_n=a_0$ であり、$a_0=1$ とおけば特殊解は$$y_1=\frac{1}{1-x}$$となります。
もう1つの特殊解 $y_2$ については階数低減法すなわち$$y_2=\frac{u(x)}{1-x}$$を微分方程式に代入することで求まります。
階数低減法の参考記事
これにより$$y_2=\frac{\log x}{1-x}$$と求まるので一般解は$$y(x)=\frac{c_1\log x+c_2}{1-x}$$$r$ がちゃんと2つ出てかつ差が非整数の場合であればそれぞれの $r$ について級数解を求め、その線形結合で一般解ができあがります。しかし今の場合 $r=0$ は重解なので、これより級数解 $y_1$ を求め、階数低減法によって $y_2$ を計算しました。
$x(x-1)y^{\prime\prime}-xy'+y=0$ を解け.
$$y=\sum^\infty_{n=0}a_nx^{n+r} \; \; , \; a_0\ne 0$$を微分方程式に代入すると$$\sum^\infty_{n=0}[(n+r-1)^2a_nx^{n+r}-(n+r)(n+r-1)a_nx^{n+r-1}]=0$$最低次の項は $r(r-1)a_0=0$ なので決定方程式は $r(r-1)=0$ です。従って$$r=0,1$$となります。今回は例題3と違って $r$ が2つ出てきました。
まず $r=1$ における特殊解 $y_1$ を求めます。あらためて$$y=x\sum^\infty_{n=0}a_nx^n \; \; , \; a_0\ne 0$$を微分方程式に代入すると$$-2a_1x+\sum^\infty_{n=1}(n^2a_n-(n+2)(n+1)a_{n+1})x^{n+1}=0$$各項を調べると$$a_1 =0\; ,\; a_{n+1}=\frac{n^2}{(n+1)(n+2)}a_n$$$a_0$ に関しては何の情報もありませんので任意の定数です。$a_1=0$ ですからドミノ倒しのごとく $a_n$ はゼロとなります。よって $a_0=1$ ととると$$y_1=x$$これが1つめの特殊解です。
次に $r=0$ における特殊解を考えます。$$y=\sum^\infty_{n=0}a_nx^n \; \; , \; a_0\ne 0$$を微分方程式に代入すると $a_0=0$ であることが判明しますが仮定に矛盾するので特殊解はナシです。
これはどういうことか。$a_0=0$ ということは $x$ の1次の項から始まるわけです。つまりそれは $r=1$ の級数にほかなりません。なのでこのまま進めても結局同じ特殊解 $y_1$ を得て無駄な努力に終わります。
よって残りの特殊解 $y_2$ は階数低減法 $y_2=xu(x)$ とおいて求めましょう。最終的に一般解は$$y=c_1x+c_2(x\log x+1)$$
$4xy^{\prime\prime}+2y'+y=0$ を解け.
フロベニウス法により決定方程式は $r(2r-1)=0$ となるので$$r=0\;,\;\frac{1}{2}$$今回も $r$ が2つ得られましたが、例題4と違うのは $r$ どうしの差が非整数であるということです。
まず $r=0$ の場合$$y=\sum^\infty_{n=0}a_nx^n \; \; , \; a_0\ne 0$$を微分方程式に代入することで$$a_n=(-1)^n\frac{a_0}{(2n)!}$$なる一般項を得ます。$a_0=1$ ととれば特殊解は\begin{eqnarray*}y_1&=&\sum^\infty_{n=0}a_nx^n\\&=&\sum^\infty_{n=0}(-1)^n\frac{x^n}{(2n)!}\\&=&\sum^\infty_{n=0}(-1)^n\frac{\sqrt{x}^{2n}}{(2n)!}\\&=&\cos\sqrt{x}\end{eqnarray*}
次に $r=1/2$ の場合$$y=x^{\frac{1}{2}}\sum^\infty_{n=0}a_nx^n \; \; , \; a_0\ne 0$$を微分方程式に代入することで$$a_n=(-1)^n\frac{a_0}{(2n+1)!}$$なる一般項を得ます。$a_0=1$ ととれば特殊解は\begin{eqnarray*}y_2&=&x^{\frac{1}{2}}\sum^\infty_{n=0}a_nx^n\\&=&\sum^\infty_{n=0}(-1)^n\frac{x^{n+1/2}}{(2n+1)!}\\&=&\sum^\infty_{n=0}(-1)^n\frac{\sqrt{x}^{2n+1}}{(2n+1)!}\\&=&\sin\sqrt{x}\end{eqnarray*}
2つの特殊解は独立です。線型結合することで一般解は$$y=c_1\cos\sqrt{x}+c_2\sin\sqrt{x}$$
以上、フロベニウス法の3パターンを紹介しました。斉次の2階線型微分方程式は奥が深く、このような方法でないと解を見つけるのが困難なこともあります。フロベニウス法はまず決定方程式によって $r$ を求めることからです。それさえできれば級数法の知識でおのずと特殊解を見つけられると思います。特殊解が1つしか出てこなかったら、これまでと同様に$y_2=y_1u(x)$ でもう1つを見つければよいわけですから、3パターンを覚える必要は全くありません。
今回は級数表示で得られた解を最終的に初等関数に直せるものばかりでした。つまり級数法を用いなくても何らかの方法で、あるいは鋭い閃きで解を導き出すことができる微分方程式だったということです。しかし微分方程式の中には解が初等的に表せないものもあり、まともな解法ではお手上げです。そんなときにこの級数法は絶大な威力を発揮することになります。今後の記事で書いていきます。
次:
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。

【Amazon】常微分方程式 (技術者のための高等数学)
常微分方程式シリーズ
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。