前回の記事はコチラ:
前回と同様、複素解析の基本知識を要します(極やローラン展開、留数)。
より詳しくは下記のWhittaker & Watsonがいいです。
関数 $u(z)$ についての斉次2階線型微分方程式\begin{equation}u''+p(z)u+q(z)u=0\tag{0.1}\end{equation}における特異点 $z=a$ に対し、$(z-a)p(z)$ および $(z-a)^2q(z)$ がその点で正則になるとき、これを確定特異点(regular singular point)という。
要は「$p(z)$ は $z=a$ で正則か1位の極」「$q(z)$ は $z=a$ で正則か1位または2位の極」ということです。ただし、特異点であることが前提なので、どちらかは正則ではありません。なおここで述べている特異点には、無限遠点 $z=\infty$ が特異点である場合も含んでいます。
$u''+p(z)u+q(z)u=0$ において $p(z)$ , $q(z)$ が有理型関数であり、その方程式の特異点がすべて確定特異点であるものをフックス型微分方程式(Fuchsian equation)という。
方程式がもつ特異点が確定特異点であるかどうかは、原則として定義0Aで判定します。ただし、無限遠点 $z=\infty$ の場合は方程式(0.1)で $z=1/w$ に変換して\begin{equation}\frac{d^2u}{dw^2}+\left[\frac{2}{w}-\frac{p\left(\frac{1}{w}\right)}{w^2}\right]\frac{du}{dw}+\frac{q\left(\frac{1}{w}\right)}{w^4}u=0\tag{0.2}\end{equation}とし、$w=0$ を調べればよいです。これにより、機械的には以下の判定法となります。
● 無限遠点 $z=\infty$ で正則とは、\begin{equation}\frac{2}{w}-\frac{p\left(\frac{1}{w}\right)}{w^2}\;,\;\frac{q\left(\frac{1}{w}\right)}{w^4}\tag{0.3}\end{equation}の両者が $w=0$ で正則であるということ。換言すれば\begin{equation}2z-z^2p(z)\;,\; z^4q(z)\tag{0.4}\end{equation}が $z=\infty$ で正則ということ。
● 無限遠点 $z=\infty$ で確定特異点とは、\begin{equation}2-\frac{p\left(\frac{1}{w}\right)}{w}\;,\;\frac{q\left(\frac{1}{w}\right)}{w^2}\tag{0.5}\end{equation}の両者が $w=0$ で正則であるということ。換言すれば\begin{equation}zp(z)\;,\; z^2q(z)\tag{0.6}\end{equation}が $z=\infty$ で正則ということ。
フックス型微分方程式の特徴として、確定特異点が指定されていれば方程式の形がかなり限定されるということがありました。例題を豊富に設けたので、前回の記事もぜひ参照してください。
では今回の内容に入っていきましょう。下の本が参考になります。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
この後に出てくる3つの特異点に備えた練習、といった位置づけです。進め方は前回記事と同様なので、適宜はしょっていきます。簡単のため、係数関数 $p(z)$ , $q(z)$ は分数関数または多項式の形で表せるとします。
確定特異点a,b
$\infty$ でない確定特異点 $a,b$ をもつフックス型微分方程式は\begin{equation}u''+\left(\frac{1+\a}{z-a}+\frac{1-\a}{z-b}\right)u'+\frac{(a-b)\b}{(z-a)(z-b)}\left(\frac{1}{z-a}-\frac{1}{z-b}\right)u=0\tag{1.1}\end{equation}に限られる。ただし $\a,\b$ は定数。
$a,b$ が確定特異点より $u''+p(z)u+q(z)u=0$ に対して$$p(z)=\frac{A}{z-a}+\frac{B}{z-b}+\tilde{p}(z)$$$$q(z)=\frac{q_3(z)}{(z-a)^2(z-b)^2}+\tilde{q}(z)$$と表せます。ただし $q_3(z)$ は高々3次多項式、$\tilde{p}(z)$ , $\tilde{q}(z)$ は多項式。$\infty$ で正則なので$$2z-z^2p(z)\neq\infty\Rightarrow \frac{Az}{z-a}+\frac{Bz}{z-b}+z\tilde{p}(z)=2\quad(at\;z=\infty)$$$$z^4q(z)\neq\infty\Rightarrow \frac{q_3(z)}{(1-a/z)^2(1-b/z)^2}+z^4\tilde{q}(z)\neq\infty\quad(at\;z=\infty)$$が成り立ちます。従って$$A+B=2\;,\;q_3(z)=\mathrm{const.}\;,\; \tilde{p}(z)=\tilde{q}(z)=0$$でなくてはなりません。そこで $A=1+\a$ , $B=1-\a$ と置きなおし、$q_3(z)=\b(a-b)^2$ とすると条件を満たす方程式は$$u''+\left(\frac{1+\a}{z-a}+\frac{1-\a}{z-b}\right)u'+\frac{(a-b)^2\beta}{(z-a)^2(z-b)^2}u=0$$よって命題1Aは示されました。
$q_3(z)=\b(a-b)^2$ という定数の取り方に違和感があるかもしれません。後で理由は分かります。
確定特異点a,∞
片方が $b=\infty$ で無限遠点である場合を考えます。前回記事では $z=0,\infty$ が確定特異点である場合のフックス型方程式を求めました。それとまったく同じ方法により、次の事実が証明できます。
確定特異点 $a,\infty$ をもつフックス型微分方程式は\begin{equation}u''+\frac{A}{z-a}u'+\frac{B}{(z-a)^2}u=0\tag{1.2}\end{equation}に限られる。ただし $A,B$ は定数。
命題1Bは命題1Aとは別に求めたもので、この段階で両者に関係はありません。ところが命題1Aにおいて $b\to\infty$ とすると$$u''+\frac{1+\a}{z-a}u'+\frac{\b}{(z-a)^2}u=0$$となります。これは命題1Bそのものです。よって命題1Aは命題1Bを含んでおり、本質的に必要なのは前者だけだと分かります。したがって 「$\infty$ でない」という文言を取り去って
確定特異点 $a,b$ をもつフックス型微分方程式は\begin{equation}u''+\left(\frac{1+\a}{z-a}+\frac{1-\a}{z-b}\right)u'+\frac{(a-b)\b}{(z-a)(z-b)}\left(\frac{1}{z-a}-\frac{1}{z-b}\right)u=0\tag{1.3}\end{equation}に限られる。ただし $\a,\b$ は定数であり、$a,b$ のいずれかが $\infty$ であってもよい。
同じように確定特異点が3つの場合も考えてみましょう。
確定特異点a,b,c
$u''+p(z)u+q(z)u=0$ において確定特異点が $z=a,b,c$ であり、いずれも $\infty$ でないとします。$p(z)$ は多項式を $(z-a)(z-b)(z-c)$ で割ったものとなりますので、次のように表現しておきます。\begin{equation}p(z)=\frac{A}{z-a}+\frac{B}{z-b}+\frac{C}{z-c}+\tilde{p}(z)\tag{2.1}\end{equation}ただし $\tilde{p}(z)$ は多項式です。同様に $\tilde{q}(z)$ を多項式、 $q_5(z)$ を高々5次式として\begin{equation}q(z)=\frac{q_5(z)}{(z-a)^2(z-b)^2(z-c)^2}+\tilde{q}(z)\tag{2.2}\end{equation}なお $q(z)$ は高々2位の極なので $q_5(z)$ が $z-a$ を因数にもつ可能性もあります。
$\infty$ で正則なので $z=\infty$ において$$2z-z^2p(z)=z\left[2-\frac{A}{1-a/z}-\frac{B}{1-b/z}-\frac{C}{1-c/z}-z\tilde{p}(z)\right]$$が発散しないためには \begin{equation}\tilde{p}(z)=0\;,\; A+B+C=2\tag{2.3}\end{equation}(2.1)より $A,B,C$ はそれぞれ $z=a,b,c$ における $p(z)$ の留数ともいえます。その和が $2$ であるというわけです。
$q(z)$ に対しては $z=\infty$ において$$z^4q(z)=\frac{q_5(z)/z^2}{(1-a/z)^2(1-b/z)^2(1-c/z)^2}+z^4\tilde{q}(z)$$が発散してはいけないので \begin{equation}\tilde{q}(z)=0\;,\; q_5(z)=q_0+q_1z+q_2z^2\tag{2.4}\end{equation}と書けます。$q_5(z)$ は高々2次式であることが分かったので\begin{eqnarray}q(z)&=&\frac{q_5(z)}{(z-a)^2(z-b)^2(z-c)^2}\\ &=& \frac{1}{(z-a)(z-b)(z-c)}\left(\frac{A'}{z-a}+\frac{B'}{z-b}+\frac{C'}{z-c}\right)\tag{2.5}\end{eqnarray}と書き換えることができます。ここで $A',B',C'$ はそれぞれ $z=a,b,c$ における $(z-a)$$(z-b)$$(z-c)$$q(z)$ の留数ともいえます。
さて、以上により $p(z)$ , $q(z)$ の形が定まりました。すなわち条件を満たすフックス型方程式は\begin{eqnarray}&&u''+\left(\frac{A}{z-a}+\frac{B}{z-b}+\frac{C}{z-c}\right)u'\\&&\quad+\frac{1}{(z-a)(z-b)(z-c)}\left(\frac{A'}{z-a}+\frac{B'}{z-b}+\frac{C'}{z-c}\right)u=0\tag{2.6}\end{eqnarray}ただし $A+B+C=2$ です。
ここで終わっても構わないのですが、定数を取り直します。特異点のいずれかが $\infty$ であっても成り立つ形にしたいのと、解の構造をより端的に示すために\begin{equation}A=1-\a-\a'\;,\;B=1-\b-\b'\;,\;C=1-\g-\g'\tag{2.7}\end{equation}\begin{equation}A'=\a\a'(a-b)(a-c)\;,\;B'=\b\b'(b-a)(b-c)\;,\;C'=\g\g'(c-a)(c-b)\tag{2.8}\end{equation}と取り直しましょう。結果として次の事実が成り立ちます。
$\infty$ でない確定特異点 $a,b,c$ をもつフックス型微分方程式は\begin{eqnarray}&&u''+\left(\frac{1-\a-\a'}{z-a}+\frac{1-\b-\b'}{z-b}+\frac{1-\g-\g'}{z-c}\right)u'\\&&\quad+\left(\frac{\a\a'(a-b)(a-c)}{z-a}+\frac{\b\b'(b-a)(b-c)}{z-b}+\frac{\g\g'(c-a)(c-b)}{z-c}\right)\\&&\quad\quad\quad\times\frac{u}{(z-a)(z-b)(z-c)}=0\end{eqnarray}に限られる。ただし $\a+\a'+\b+\b'+\g+\g'=1$ .
確定特異点a,b,∞
特異点の1つが $z=\infty$ である場合を考えます。$a,b,\infty$ が確定特異点としましょう。
$a,b$ が確定特異点なので高々3次の式 $q_3(z)$ を用いて\begin{equation}p(z)=\frac{A}{z-a}+\frac{B}{z-b}+\tilde{p}(z)\tag{2.9}\end{equation}\begin{equation}q(z)=\frac{q_3(z)}{(z-a)^2(z-b)^2}+\tilde{q}(z)\tag{2.10}\end{equation}$\infty$ で確定特異点なので、$z=\infty$ で $zp(z)$ , $z^2q(z)$ が正則であればよいです。よって $\tilde{p}(z)=\tilde{q}(z)=0$ であり、$q_3(z)$ は2次以下の式となります。したがってこのときの微分方程式は\begin{eqnarray}&&u''+\left(\frac{A}{z-a}+\frac{B}{z-b}\right)u'\\&&\quad+\left(\frac{A'}{z-a}+\frac{B'}{z-b}+C'\right)\frac{u}{(z-a)(z-b)}=0\end{eqnarray}定数を$$A=1-\a-\a'\;,\;B=1-\b-\b'$$$$A'=\a\a'(a-b)\;,\;B'=\b\b'(b-a)\;,\;C'=\g\g'$$と取り直すと\begin{eqnarray}&&u''+\left(\frac{1-\a-\a'}{z-a}+\frac{1-\b-\b'}{z-b}\right)u'\\&&\quad+\left(\frac{\a\a'(a-b)}{z-a}+\frac{\b\b'(b-a)}{z-b}+\g\g'\right)\frac{u}{(z-a)(z-b)}=0\end{eqnarray}5つの任意定数を6つの定数に取り直したので、$\a+\a'+\b+\b'+\g+\g'=1$ なる制約を加えましょう。すると命題2Aの式で $c\to\infty$ としたものと同じ式になっていることが分かります。
以上から命題2Aは、確定特異点が $\infty$ の場合も含めて成り立っていますので、次の定理がいえます。
確定特異点 $a,b,c$ をもつフックス型微分方程式は\begin{eqnarray}&&u''+\left(\frac{1-\a-\a'}{z-a}+\frac{1-\b-\b'}{z-b}+\frac{1-\g-\g'}{z-c}\right)u'\\&&\quad+\left(\frac{\a\a'(a-b)(a-c)}{z-a}+\frac{\b\b'(b-a)(b-c)}{z-b}+\frac{\g\g'(c-a)(c-b)}{z-c}\right)\\&&\quad\quad\quad\times\frac{u}{(z-a)(z-b)(z-c)}=0\end{eqnarray}に限られる。ただし $\a+\a'+\b+\b'+\g+\g'=1$ であり、$a,b,c$ のいずれかが $\infty$ であってもよい。
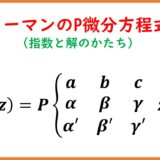
定理3の微分方程式をリーマンのP方程式(Riemann P-differential equation)あるいはPapperitz方程式といいます。$\a,\a'$ を「確定特異点 $a$ に属するexponent(指数)」とよびます。あるいはcharacteristic exponent(特性指数)とも。また、この微分方程式の解をまとめて\begin{equation}u(z)=P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}\tag{3.1}\end{equation}と書き、リーマンのP記法といいます。
$\a,\a'$ をこのように明示するということは、何らかの重要な意味をもっているはずです。実は「指数」という呼称こそが、わざわざこんなややこしい定数を設けた理由を物語っているのです。詳細は次回の記事で説明します。
2階に限らない、より一般的な議論についてはE.G.C.Poole,Introduction to the Theory of Linear Differential Equations(1936)をネットで閲覧することができます。本も売っています。

Introduction to the Theory of Linear Differential Equations
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。