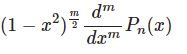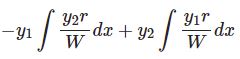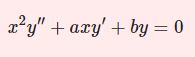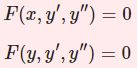3階以上の微分方程式であろうと基本はこれまでの2階微分と変わらない。よってこれまでのようにパターンを網羅的に見るのではなく、2階までのやりかたの延長で考えられるんだという例を挙げて終わろうと思う。
$$y^{(n)}+p_{n-1}(x)y^{(n-1)}+\cdots+p_0(x)y=r(x)$$$r(x)=0$ なら斉次方程式，$r(x)\neq 0$ なら非斉次方程式という．
$x^3y^{\prime\prime\prime}-3x^2y^{\prime\prime}+6xy'-6y=0$ を解け．初期値を $y(1)=2\;,\;y'(1)=1\;,\;y^{\prime\prime}(1)=-4$ とする．
オイラー・コーシーの方程式については過去記事参照。
2階のオイラー・コーシー方程式と同様に試行解 $y=x^m$ を代入します。\begin{eqnarray*}&&[m(m-1)(m-2)-3m(m-1)+6m-6]x^m=0\\\Leftrightarrow && (m-1)(m-2)(m-3)=0\\ \Leftrightarrow && m=1,2,3\end{eqnarray*}よって一般解は$$y=ax+bx^2+cx^3$$となりますが、初期値を代入して計算することにより$$y=2x+x^2-x^3$$
$x=e^t$ と変数変換して定数係数へ帰着させる方法もあります。
$y^{(5)}-3y^{(4)}+3y^{\prime\prime\prime}-y^{\prime\prime}=0$ を解け．
定数係数の方程式について、および試行解が重根になるケースは過去記事参照。
定数係数の斉次方程式なので試行解 $e^{\lambda x}$ を代入します。すると$$\lambda^5-3\lambda^4+3\lambda^3-\lambda^2=0$$を得ます。もとの微分方程式とそっくりな形をしていることを確認してください。この5次式を変形して$$(\lambda -1)^3\lambda^2=0$$さて問題の微分方程式は$5$階ですので特殊解は$5$つ必要です。このままでは $\lambda=0,1$ であり、特殊解 $y=e^0,e^x$ の2つしか得られません。
残りの特殊解をどうするか。2階のときに重解だったときの方法を説明しました。それと同様にやります。
まず重解となっている $\lambda =0$ ですが、これにより得られる $y_1=e^0=1$ およびこれに $x$ を乗じて得られる $y_2=x$ が特殊解となります。
次に3重解になっている $\lambda =1$ です。まず $y_3=e^x$ およびこれに $x$ を乗じて得られる $y_4=xe^x$ およびさらに $x$ を乗じて得られる $y_5=x^2e^x$ が特殊解となります。
$y_1$ から $y_5$ まですべて代入してみると、ちゃんと解であることが分かります。よって一般解は$$y=c_1+c_2x+c_3e^x+c_4xe^x+c_5x^2e^x$$
$y^{\prime\prime\prime}+3y^{\prime\prime}+3y'+y=30e^{-x}$ を解け．
右辺が0でないので非斉次方程式です。なので右辺をゼロとした場合の解を求め、非斉次の特殊解を探して加算するというのが王道です。特殊解の探し方はある程度パターン化された試行解を代入してみるという方法がありました（過去記事）。
まず右辺を$0$とした斉次解を求めます。これは定数係数の方程式ですから $e^{\lambda x}$ を代入すると $\lambda=-1$ の3重解を得ますので、先の例題２と同様にして斉次一般解は$$y_0=(a+bx+cx^2)e^{-x}$$
非斉次方程式の一般解はこの斉次一般解 $y_0$ に特殊解 $y_p$ を加えたものです。では $y_p$ は一体何なんだというと $y_p=kx^3e^{-x}$ の形をしていると予想されます。どうしてこうなるというのはおいといて、実際にこれを試行解としてもとの微分方程式に代入すると\begin{eqnarray*}&&y^{\prime\prime\prime}_p+3y^{\prime\prime}_p+3y'_p+y_p=30e^{-x}\\\Leftrightarrow&& ke^{-x}[(-x^3+9x^2-18x+6)+3(x^3-6x^2+6x)+3(-x^3+3x^2)+x^3]=30e^{-x}\\\Leftrightarrow&& 6k=30\\\Leftrightarrow&& k=5\end{eqnarray*}ピシッと決まりました。したがって$$y_p=5x^3e^{-x}$$$$\therefore\quad y=(a+bx+cx^2+5x^3)e^{-x}$$
どの例題も2階でやった方法の延長にあることが分かったと思います。
ここまでの10記事で1階、2階、3階・・・の基本的な微分方程式の説明が終わりました。今後は無限級数を使って解く特殊な方程式を紹介します。
次：
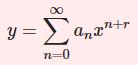【D11】級数法・フロベニウス法
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
