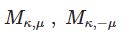ルジャンドルの微分方程式\begin{equation}(1-x^2)y^{\prime\prime}-2xy'+\nu(\nu+1)y=0\tag{1}\end{equation}の特殊解を偶奇統一形式にする.そのように表される関数を第1種ルジャンドル関数という.
本記事は筆者が無知な頃に書いたものであり、曖昧さはありますが、内容自体には特に問題ありません。正確な理解をしたい場合は確定特異点について詳しく書いたシリーズをご覧ください。
こちらで見たようにルジャンドルの微分方程式(1)の解を $x$ のべきとした級数法により解くと\begin{eqnarray*}A_\nu(x)&\equiv&\frac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\pi}\Gamma(\frac{\nu}{2}+1)} {}_2F_1\left[ \begin{matrix}\frac{\nu+1}{2},-\frac{\nu}{2}\\\frac{1}{2}\end{matrix};x^2 \right] \\ B_\nu(x)&\equiv& \frac{\Gamma(\frac{\nu}{2}+1)}{\sqrt{\pi}\Gamma(\frac{\nu+1}{2})} x\;{}_2F_1\left[\begin{matrix}\frac{\nu}{2}+1,\frac{1-\nu}{2}\\\frac{3}{2}\end{matrix};x^2 \right] \end{eqnarray*}の特殊解2つが求まり,一般解は$$y(x)=aA_\nu(x)+bB_\nu(x)$$となるのでした.
ここで$$ {}_2F_1\left[\begin{matrix}a,b\\c\end{matrix}\;;x\right] \equiv\sum_{n=0}^\infty\frac{(a)_n(b)_n}{(c)_n}\frac{x^n}{n!}$$なおポッホハマー記号は$$(x)_n\equiv x(x+1)\cdots(x+n-1)\;,\quad (x)_0=1$$上記の解の求め方は過去記事参照(ただし $A_\nu$ , $B_\nu$ の係数が上と異なります)。
特殊解 $A_\nu$ , $B_\nu$ は $\nu$ が整数のときだけでなく一般の実数に対応しています.特に $\nu$ が偶数ときは $A_\nu$ が $\nu$ 次多項式で $B_\nu$ が無限級数($\log$ など),$\nu$ が奇数のときはその逆となるのです.それらの多項式を $\nu$ 次のルジャンドル多項式というのでした.
| $\nu=2m$ | $\nu=2m+1$ | |
| $A_\nu(x)$ | 多項式 | 無限級数 |
| $B_\nu(x)$ | 無限級数 | 多項式 |
もう少し具体的にいうとルジャンドル多項式 $P_n(x)$ は\begin{equation}P_n(x)=\begin{cases}(-1)^{\frac{n}{2}}A_n(x)\quad(n:\mathrm{even})\\(-1)^{\frac{n-1}{2}}B_n(x)\quad(n:\mathrm{odd})\end{cases}\tag{2}\end{equation}と表されます.表現が偶奇で別々になってしまっていますね.
この偶奇を統一した表現がほしい!というのが本稿の動機です.ルジャンドル多項式の統一記法はあって$$P_n(x)=\frac{1}{2^n}\sum_{m=0}^{[n/2]}(-1)^m\frac{(2n-2m)!}{m!(n-m)!(n-2m)!}x^{n-2m}$$と書けるのですが,この記法は $n\in\mathbb{Z^+}$ つまり多項式のときだけ成立するものであり,あくまで「ルジャンドル多項式」であって,ルジャンドル微分方程式の一般的な特殊解ではない.大事なのは(1)の $\nu$ が実数のときも含んだ解です.$\nu$ が整数のみならず実数でなおかつ $\nu$ が整数のときのルジャンドル多項式が偶奇統一されるような記述をしたいわけです.
特殊解を任意に線型結合したものも特殊解なのですから,以下のように作為的な結合で定義します.\begin{equation}P_\nu(x)\equiv\cos\frac{\nu\pi}{2}A_\nu(x)+\sin\frac{\nu\pi}{2}B_\nu(x)\tag{3}\end{equation}これは $\nu$ が非負整数のときの(2)と一致しています.よって $P_\nu(x)$ は $\nu$ が実数で成り立ち,かつ整数のときは偶奇統一された表現であるということになります.一応目標は達せられたわけです.しっかり書き下すと$$P_\nu(x)=\cos\frac{\nu\pi}{2}\frac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\pi}\Gamma(\frac{\nu}{2}+1)} {}_2F_1\left[ \begin{matrix}\frac{\nu+1}{2},-\frac{\nu}{2}\\\frac{1}{2}\end{matrix};x^2 \right] + \sin\frac{\nu\pi}{2} \frac{\Gamma(\frac{\nu}{2}+1)}{\sqrt{\pi}\Gamma(\frac{\nu+1}{2})} x\;{}_2F_1\left[\begin{matrix}\frac{\nu}{2}+1,\frac{1-\nu}{2}\\\frac{3}{2}\end{matrix};x^2 \right] $$
とはいってもこの解は形としてはごちゃっとしています.そこで『岩波数学公式III』のルジャンドル関数の項目を見ると,$P_\nu$ が $1-x$ のべきとして与えられており,すっきりとした形になっていました.その手があったかと思い,実際に導出しました.
微分方程式(1)において $(1-x)$ のべきで級数法を適用します(最初フロベニウス法でやってしまって $r=0$ の重解を得たという徒労). $$y=\sum_{n=0}^\infty a_n(1-x)^n$$とおけば\begin{eqnarray*}y'&=&-\sum_{n=0}^\infty na_n(1-x)^{n-1}\\y^{\prime\prime}&=&\sum_{n=0}^\infty n(n-1)a_n(1-x)^{n-2}\end{eqnarray*}これらを方程式(1)に代入して$$\begin{cases}a_0\; : \;任意\\a_{n+1}=\displaystyle\frac{(n+\nu+1)(n-\nu)}{2(n+1)^2}a_n\quad (n \ge 0)\end{cases}$$なる漸化式を得ます.漸化式を繰り返し用いて一般項は\begin{eqnarray*}a_n&=&\frac{(\nu+n)(-\nu+n-1)}{2n^2}a_{n-1}\\&\vdots&\\ &=& \frac{(\nu+1)_n(-\nu)_n}{2^n(n!)^2}a_0\\ &=& \frac{(\nu+1)_n(-\nu)_n}{2^n(1)_nn!}a_0\quad(n\ge 0)\end{eqnarray*}
したがって $a_0=1$ とおくと特殊解は \begin{eqnarray*} y&=&\sum_{n=0}^\infty a_n(1-x)^n\\ &=& \sum_{n=0}^\infty \frac{(\nu+1)_n(-\nu)_n}{2^n(1)_nn!} (1-x)^n \\&=& \sum_{n=0}^\infty \frac{(\nu+1)_n(-\nu)_n}{(1)_nn!} \left(\frac{1-x}{2}\right)^n \\&=& {}_2F_1\left[\begin{matrix}\nu+1,-\nu\\1\end{matrix}\;;\frac{1-x}{2}\right]\end{eqnarray*}と求まります.実は(3)の $P_\nu$ と同じで\begin{equation}P_\nu(x)= {}_2F_1\left[\begin{matrix}\nu+1,-\nu\\1\end{matrix}\;;\frac{1-x}{2}\right] \tag{4}\end{equation}(3)よりも明らかに表記はすっきりしています.
(4)の $\nu$ に整数を代入すると\begin{eqnarray*}P_0(x)&=&1\\P_1(x)&=&x\\P_2(x)&=&\frac{3x^2-1}{2}\end{eqnarray*}であり,確かにルジャンドル多項式と一致します.しかも(4)なら一瞬でルジャンドル関数の要件 $P_\nu(1)=1$ を満たすと分かります.
そうなると(4)は微分方程式(1)の特殊解として最重要のものとして位置付けていいのではないでしょうか.
- $\nu\in\mathbb{Z}$ でルジャンドル多項式となる
- $\nu$ が偶数でも奇数でも同じ表記
- 式がシンプル。超幾何関数の前に定数がないのも美しい。
実際にこれは第1種ルジャンドル関数 $P_\nu(x)$ と名付けられているため,ルジャンドルの微分方程式の代表的な特殊解と認められているのです.
じゃあ無限級数となるほうの特殊解はどうなるのだろう?$P_\nu$ の他方の特殊解を第2種ルジャンドル関数 $Q_\nu(x)$ といいます.
ついでに $Q_\nu$ も求めたい.特殊解が1つ分かっているときに便利な階数低減法を使おうと考えました.
階数低減法の解説はこちら
$Q_\nu=uP_\nu$ とおいて(1)に代入して…と挑戦しましたが,とんでもない式になってしまってやれる気がしませんでした.
そこで『岩波数学公式III』を見たところ,$Q_\nu$ は $\frac{1}{x}$ でべき展開した形となっています.なんでそうできるのかというのはフックス型方程式の理論を学べば納得できるのですが、それはさておき,これを前提とすれば級数法の応用でできそうです.$$y=\sum_{n=0}^\infty a_nx^{-n-r}$$とおくと\begin{eqnarray*}y'&=&-\sum_{n=0}^\infty (n+r)a_nx^{-n-r-1}\\y^{\prime\prime}&=&\sum_{n=0}^\infty (n+r)(n+r+1)a_nx^{-n-r-2}\end{eqnarray*}これらを(1)に代入すると恒等式$$-(r+\nu)(r-\nu-1)a_0x^{-r}-(r+\nu+1)(r-\nu)a_1x^{-r-1}+\sum_{n=0}^\infty[(n+r)(n+r+1)a_n-(n+r+\nu+2)(n+r-\nu+1)a_{n+2}]x^{-n-r-2}=0$$第一項が決定方程式で $r=-\nu,\nu+1$ となります.$r=\nu+1$ とすると恒等式の第1項は消えて$$ -2(\nu+1)a_1x^{-\nu-2}+\sum_{n=0}^\infty[(n+\nu+1)(n+\nu+2)a_n-(n+2\nu+3)(n+2)a_{n+2}]x^{-n-\nu-3}=0$$よって$$\begin{cases}a_0\; : \;任意\\a_1=0\\a_{n+2}=\displaystyle\frac{ (n+\nu+1)(n+\nu+2) }{ (n+2\nu+3)(n+2) }a_n\quad (n \ge 0)\end{cases}$$なる漸化式を得ます.1項飛ばしの漸化式ですから奇数項 $a_{2m-1}=0$ で,偶数項は\begin{eqnarray*}a_{2m}&=&\frac{ (2m+\nu-1)(2m+\nu) }{ (2m+2\nu+1)2m }a_{2m-2}\\ &=& \frac{ (2m+\nu-1)(2m+\nu-3)\cdots(1+\nu)\times (2m+\nu) (2m+\nu-2)\cdots(2+\nu)}{ (2m+2\nu+1)(2m+2\nu-1)\cdots(2\nu+3)\times(2m)!! }a_0\\ &=& \frac{ (m-1+\frac{\nu+1}{2})(m-2+\frac{\nu+1}{2})\cdots(\frac{1+\nu}{2})\times (m+\frac{\nu}{2})(m-1+\frac{\nu}{2})\cdots(1+\frac{\nu}{2})}{ (m+\nu+\frac{1}{2})(m+\nu-\frac{1}{2})\cdots(\nu+\frac{3}{2})\times(m)! }a_0\\ &=&\frac{(\frac{\nu+1}{2})_m(\frac{\nu}{2}+1)_m}{(\nu+\frac{3}{2})_mm!}a_0\end{eqnarray*}
よって特殊解は\begin{eqnarray*}y&=&\sum_{m=0}^\infty a_{2m}x^{-2m-\nu-1}\\&=& \frac{a_0}{x^{\nu+1}} \sum_{m=0}^\infty \frac{(\frac{\nu+1}{2})_m(\frac{\nu}{2}+1)_m}{(\nu+\frac{3}{2})_mm!} \frac{1}{x^{2m}}\\&=& \frac{a_0}{x^{\nu+1}} {}_2F_1\left[\begin{matrix}\frac{\nu+1}{2},\frac{\nu}{2}+1\\\nu+\frac{3}{2}\end{matrix}\;;\frac{1}{x^2}\right]\end{eqnarray*}
第2種ルジャンドル関数 $Q_\nu$ は $a_0$ を定めて$$Q_\nu(x)=\frac{\sqrt{\pi}\Gamma(\nu+1)}{\Gamma(\nu+\frac{3}{2})}\frac{1}{(2x)^{\nu+1}} {}_2F_1\left[\begin{matrix}\frac{\nu+1}{2},\frac{\nu}{2}+1\\\nu+\frac{3}{2}\end{matrix}\;;\frac{1}{x^2}\right] $$となります.
第1種ルジャンドル関数$$ P_\nu(x)= {}_2F_1\left[\begin{matrix}\nu+1,-\nu\\1\end{matrix}\;;\frac{1-x}{2}\right] $$
第2種ルジャンドル関数 $$Q_\nu(x)=\frac{\sqrt{\pi}\Gamma(\nu+1)}{\Gamma(\nu+\frac{3}{2})}\frac{1}{(2x)^{\nu+1}} {}_2F_1\left[\begin{matrix}\frac{\nu+1}{2},\frac{\nu}{2}+1\\\nu+\frac{3}{2}\end{matrix}\;;\frac{1}{x^2}\right] $$
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。