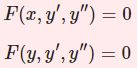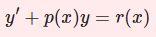クレローの微分方程式は１階非線型微分方程式です。これは一般解のほかに「特異解」という変な解をもちます。一般解には任意定数がつきますが、任意定数に何を代入しても得られない解を「特異解」といいます。特異解は一般解の包絡線になっています。
常微分シリーズ過去記事
【D1】１階線型微分方程式の解法
【D2】ベルヌーイの微分方程式
\begin{equation}y=xy'+f(y')\tag{1}\end{equation}
私としては微分方程式を学習したときに出会って以降、まったく見たことがない方程式です。応用例があれば知りたいです。
この方程式の解はどう求まるでしょうか？両辺を微分して\begin{eqnarray*}& &y'=y'+xy^{\prime\prime} +f'(y')y^{\prime\prime} \\ &\Leftrightarrow & xy^{\prime\prime}+f'(y')y^{\prime\prime}=0\\ &\Leftrightarrow & y^{\prime\prime} [x+f'(y')]=0\\[1em] &\therefore & \begin{cases}y^{\prime\prime}=0\;\;\mathrm{or}\\x+f'(y')=0\end{cases}\end{eqnarray*}$y^{\prime\prime}=0$ について解くと $y(x)=cx+c_0$ となります（$c,c_0$ は任意定数）。これをもとの微分方程式(1)に代入すると $c_0=f(c)$ を得ますから、一般解は$$y(x)=cx+f(c)$$ となります。一階の微分方程式ですから、任意定数が１つなのは以前までの話と合致していますね。
さらにこれとは別に $x+f^\prime(y^\prime)=0$ からは特異解を得ます。どのような解かは $f$ 次第です。この特異解は上に示した一般解には含まれていません。つまりクレローの方程式は一般解と特異解をともに示して初めて完全に解けたことになります。
大切なのは解を覚えることではなく、「方程式(1)を $x$ で微分する」のがエッセンスです。
一般解 $y(x)=cx+f(c)$ は定数 $c$ を変化させることで直線の集合をあらわすことになります。これらの直線は実は特異解（曲線）の包絡線になっています。あとの例題で確認します。
包絡線について
クレローの方程式とは無関係に、一般的な包絡線の求め方を補足しておきます。直線 $y=cx+f(c)$ を変形すると $F_c(x,y)\equiv cx+f(c)-y=0$ となります。包絡線は以下の連立方程式$$\begin{cases} F_c(x,y)=0\\\displaystyle\frac{\partial F_c}{\partial c}=0\end{cases}$$から $c$ を消せば求まります。
$y=xy'+\displaystyle\frac{1}{y'}$ を解け。
両辺を微分すると $y^{\prime\prime}\left[x-\displaystyle\frac{1}{{y'}^2}\right]=0$ です。よって方程式は以下の２つに分けて考えられます。$$\begin{cases}y^{\prime\prime}=0\\x-\displaystyle\frac{1}{{y'}^2}=0\end{cases}$$これらを解くことにより $y^{\prime\prime}=0$ から一般解$$y(x)=cx+\frac{1}{c}$$を得て、$x-\displaystyle\frac{1}{{y^\prime}^2}=0$ からは特異解$$y(x)=\pm 2\sqrt{x}$$を得ます(１階微分なので積分定数はでてきますが、もとの微分方程式に代入すると定数は $0$ だと分かります)．
特異解のうち $y(x)=2\sqrt{x}$ のほうだけ考えてみます。これを微分して傾きを求めることで、点 $x=1/c^2>0$ における接線の式は$$y=c(x-\frac{1}{c^2})+2\sqrt{\frac{1}{c^2}}$$と分かります。整理することで$$y=cx+\frac{1}{c}$$$c>0$ は任意ですからこの式は特異解があらわす曲線の接線を集めたものです。そしてこれは先ほど求めた一般解と同じです。特異解が一般解の包絡線をあらわすことがイメージできるかと思います。下にGeogebraで描いたグラフを載せます。ちゃんと接していて感動しました。
厳密に包絡線になっているか確認します。直線群 $y=cx+\frac{1}{c}$ より $F_c(x,y)=cx+\frac{1}{c}-y$ とおくと包絡線を導く連立方程式は$$\begin{cases} F_c(x,y)=0\\\displaystyle\frac{\partial F_c}{\partial c}=0\end{cases}$$すなわち$$\begin{cases} cx+\displaystyle\frac{1}{c}-y=0\\x-\displaystyle\frac{1}{c^2}=0\end{cases}$$下の式から $c=\pm\frac{1}{\sqrt{x}}$ となりますので上の式へ代入すると$$y=\pm 2\sqrt{x}$$
微分方程式$$y=xy'-\frac{y'}{\sqrt{1+y'^2}}$$の解について、一般解はどのような直線か。またアステロイド $x^{\frac{2}{3}}+y^{\frac{2}{3}}=1$ は特異解であることを示せ。
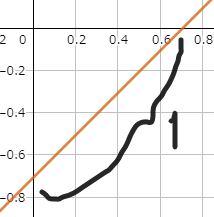
両辺を微分すると$$y^{\prime\prime}\left[x-\frac{1}{(1+y'^2)^\frac{3}{2}}\right]=0$$を得ます。よって方程式は以下の２つに分けて考えられます。$$\begin{cases}y^{\prime\prime}=0\\x-\displaystyle\frac{1}{(1+y'^2)^\frac{3}{2}}=0\end{cases}$$上の方からは $y=cx+c_0$ を得ますが、もとの方程式に代入することで $c_0=-\frac{c}{\sqrt{1+c^2}}$ であることが分かります。よって一般解は$$y(x)=cx -\frac{c}{\sqrt{1+c^2}} $$という直線です。この直線は $(\frac{1}{\sqrt{1+c^2}},0)$ および $(0,-\frac{c}{\sqrt{1+c^2}})$ を通りますので以下のようなグラフとなります。$x$ 軸と $y$ 軸の間にある部分の長さが常に $1$ であることが確認できます。
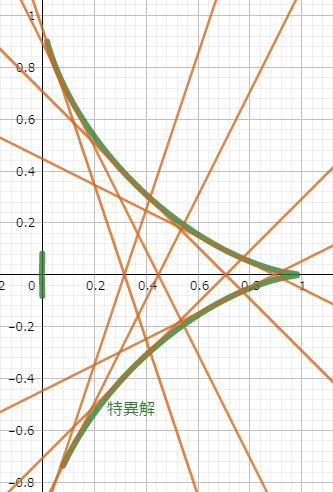
さて特異解の話へ移ります。これをまともに解くのは面倒ですが、アステロイドであることを示すのは容易です。アステロイドの式 $ x^{\frac{2}{3}}+y^{\frac{2}{3}}=1 $ が特異解の満たす式 $x-\displaystyle\frac{1}{(1+y'^2)^\frac{3}{2}}=0 $ を満足していることを示します。アステロイドの式を微分すると$$\frac{2}{3}x^{-\frac{1}{3}}+\frac{2}{3}y^{-\frac{1}{3}}y'=0$$整理して$$y'=-\frac{y^\frac{1}{3}}{x^\frac{1}{3}}$$2乗すると$$y'^2=\frac{y^\frac{2}{3}}{x^\frac{2}{3}}$$1を加えます。$$1+y'^2=\frac{x^\frac{2}{3}+y^\frac{2}{3}}{x^\frac{2}{3}}=\frac{1}{x^\frac{2}{3}}$$$$\therefore\quad x= \frac{1}{(1+y'^2)^\frac{3}{2}} $$よってアステロイドは特異解です。下図のとおり、一般解(直線)は特異解の包絡線です。
$$y=xy'+\frac{y'^2}{2}$$の一般解と特異解を求めよ。また特異解が一般解の包絡線になっていることを示せ。
両辺を微分すると$$y^{\prime\prime}[x+y']=0$$を得ます。
一般解は$$y=cx+\frac{c^2}{2}$$特異解は$$y=-\frac{x^2}{2}$$と求まります。
では包絡線になっていることを示しましょう。直線群 $F_c(x,y)=cx-y+\frac{c^2}{2}=0$ とその $c$ 微分でできる連立方程式$$ cx-y+\frac{c^2}{2}=0 \;,\; c+x=0$$から $c$ を消去すると$$y=-\frac{x^2}{2}$$となります。これは特異解と一致しています。よって特異解は包絡線です。
次回：
【D4】Chrystalの微分方程式と包絡線
本記事では、下記の本を大いに参考にしています。厳密性はほどほどに、なるべくたくさんの演習問題が用意されています。産業や自然界における事例も豊富。数学科以外の理学部・工学部生にオススメです。
【Amazon】常微分方程式 (技術者のための高等数学)
常微分シリーズ
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。