ここまでの流れは過去記事参照:
フックス型微分方程式と確定特異点2 (RiemannのP方程式)
3つの確定特異点をもつ2階フックス型微分方程式を「リーマンのP微分方程式」というのでした。
リーマンのP微分方程式\begin{eqnarray}&&u''+\left(\frac{1-\a-\a'}{z-a}+\frac{1-\b-\b'}{z-b}+\frac{1-\g-\g'}{z-c}\right)u'\\&&\quad+\left(\frac{\a\a'(a-b)(a-c)}{z-a}+\frac{\b\b'(b-a)(b-c)}{z-b}+\frac{\g\g'(c-a)(c-b)}{z-c}\right)\\&&\quad\quad\quad\times\frac{u}{(z-a)(z-b)(z-c)}=0\tag{0.1}\end{eqnarray}(ただし $\a+\a'+\b+\b'+\g+\g'=1$)
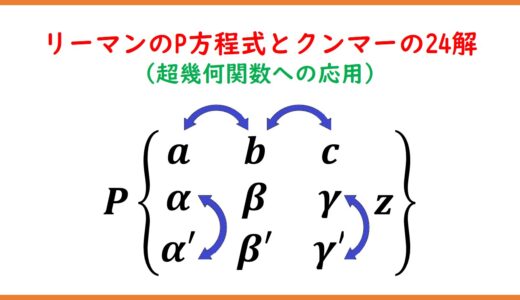
の6つの特殊解は$$(z-a)^{\a}\sum_{n=0}^\infty a_n(z-a)^{n}\quad,\quad (z-a)^{\a'}\sum_{n=0}^\infty a'_n(z-a)^{n}$$$$(z-b)^{\b}\sum_{n=0}^\infty b_n(z-b)^{n}\quad,\quad (z-b)^{\b'}\sum_{n=0}^\infty b'_n(z-b)^{n}$$$$(z-c)^{\g}\sum_{n=0}^\infty c_n(z-c)^{n}\quad,\quad (z-c)^{\g'}\sum_{n=0}^\infty c'_n(z-c)^{n}$$と表され、解全体を$$u(z)=P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}$$と表記する。
以上の事実は、いずれかの特異点を $\infty$ としても成り立つ。
(0.1)はわざわざわかりにくい定数の取り方をしているように見えますが、確定特異点 $a,b,c$ とそれに属するそれぞれの指数 $\a,\a'$ ; $\b,\b'$ ; $\g,\g'$ が解の形をよく表しています。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
微分方程式\begin{equation}(1-z^2)u''-2zu'+6u=0\tag{1.1}\end{equation}を考えましょう。割り算して $u''+p(z)u'+q(z)u=0$ の形式にします。$$u''+\frac{2z}{z^2-1}u'-\frac{6}{z^2-1}u=0$$$zp(z)$ , $z^2q(z)$ が $z=\infty$ で正則なので確定特異点は $1,-1,\infty$ です。さらに変形すると\begin{equation}u''+\left(\frac{1}{z-1}+\frac{1}{z+1}\right)u'+(-6)\frac{u}{(z-1)(z+1)}=0\tag{1.2}\end{equation}(0.1)と比較すると、確定特異点 $a=1$ に属する指数 $\a=\a'=0$ , $b=-1$ に属する指数 $\b=\b'=0$ , $c=\infty$ に属する指数 $\g=3$ , $\g'=-2$ となります。よって(1.1)の解全体は\begin{equation}u(z)=P\left\{\begin{matrix}1 & -1 & \infty\\0 & 0 & 3\\0 & 0 & -2\end{matrix}\;z\right\}\tag{1.3}\end{equation}と表現されます。
具体的に解を求めてみましょう。6パターンやるのは面倒なので$$\sum_{n=0}^\infty a_n(z-1)^n \;,\; \sum_{n=0}^\infty c_n\left(\frac{1}{z}\right)^{n+3}$$の形のものを導きます。独立なこの2つを線型結合すれば一般解ができあがります。
(i) 1つめの級数を(1.1)に代入すると\begin{eqnarray}&&6a_0-2a_1+(4a_1-8a_2)(z-1)\\&&-\sum_{n=2}^\infty\left[(n+3)(n-2)+2(n+1)(n-1)a_{n+1}\right](z-1)^n=0\tag{1.4}\end{eqnarray}恒等的に成立するから$$3a_0=a_1\;,\; 2a_2=a_1$$$$a_{n+1}=-\frac{(n-2)(n+3)}{2(n-1)(n+1)}a_n\quad(n\ge2)$$すると $a_3=a_4=\cdots=0$ なので多項式$$a_0+3a_0(z-1)+\frac{3}{2}a_0(z-1)^2$$と分かります。展開して任意定数 $a_0=1$ と定めると\begin{equation}u_1(z)=\frac{1}{2}\left(3z^2-1\right)\tag{1.5}\end{equation}なる特殊解を得ます。
(ii) 2つめは(1.1)を反転変換 $w=1/z$ して\begin{equation}(w^2-1)\frac{d^2u}{dw^2}+2w\frac{du}{dw}+\frac{6}{w^2}u=0\tag{1.6}\end{equation}これに $\sum c_n w^{n+3}$ を代入すると$$c_1=0\;,\;c_{n+2}=\frac{(n+3)(n+4)}{(n+2)(n+7)}c_n\quad(n\ge0)$$$c_1=c_3=\cdots=0$ です。$c_0=1$ ととって\begin{equation}u_2(z)=\frac{1}{z^3}+\frac{3\cdot4}{2\cdot7}\frac{1}{z^5}+\frac{3\cdot4\cdot5\cdot6}{2\cdot4\cdot7\cdot9}\frac{1}{z^7}+\cdots\tag{1.7}\end{equation}なる解を得ます。(1.7)は初等函数では表せません。
このようにフロベニウス法によって特殊解2つを導出できました。$u_1(z)$ をルジャンドル多項式(第1種ルジャンドル関数)、$u_2(z)$ を第2種ルジャンドル関数といいます。
複素関数論で現れるメビウス変換(Möbius transformation)とは、\begin{equation}\zeta=\frac{rz+s}{pz+q}\;,\quad rq-ps\neq0\tag{2.1}\end{equation}なる変数変換のことです。一次分数変換ともよばれます。$rq-ps=0$ ではただの定数になってしまうので除外しています。
前回の記事では確定特異点を2つもつフックス型方程式が、メビウス変換により、特異点が移る以外は不変であることを示しました。今回は(0.1)で同様の議論をしましょう。
といっても(2.1)の変換をもろにやろうとすると、かなりややこしい式になってゴールが見えないまま日が暮れてしまうかもしれません。そこで(2.1)をばらして考えます。すなわち\begin{equation}w=\frac{rz+s}{pz+q}=\frac{r}{p}+\frac{\frac{r}{p}\left(\frac{s}{r}-\frac{q}{p}\right)}{z+\frac{q}{p}}\tag{2.2}\end{equation}とすれば $z\to w$ の変換は\begin{eqnarray*}w_1&=&z+\frac{q}{p}\quad(平行移動)\\w_2&=&\frac{1}{w_1}\quad(反転)\\w_3&=&\frac{r}{p}\left(\frac{s}{r}-\frac{q}{p}\right)w_2\quad(拡大・回転)\\w_4&=&\frac{r}{p}+w_3\quad(平行移動)\end{eqnarray*}これらはすべてメビウス変換です。したがって平行移動(足し算)、拡大・回転(定数倍)、反転(逆数)のそれぞれでP方程式(0.1)が不変なら、任意のメビウス変換(2.1)でP方程式が不変だいえます。確定特異点が $a,b,c$ であるP方程式を、定数の値を変えて再掲します。\begin{eqnarray}&&u''+\left(\frac{A}{z-a}+\frac{B}{z-b}+\frac{C}{z-c}\right)u'\\&&\quad+\left(\frac{D(a-b)(a-c)}{z-a}+\frac{E(b-a)(b-c)}{z-b}+\frac{F(c-a)(c-b)}{z-c}\right)\\&&\quad\quad\quad\times\frac{u}{(z-a)(z-b)(z-c)}=0\tag{2.3}\end{eqnarray}(ただし $A+B+C=2$)
平行移動での不変性
(2.3)で $w=z+p$ とすると $u'\to \frac{du}{dw}$ , $u''\to\frac{d^2u}{dw^2}$ となります。ただし変換後の $u$ は $u(w-p)$ のことです。前回は改めて $f(w):=u(w-p)$ と置いていましたが、今回はそのままでいきます。(2.3)が変換されると特異点が $a+p$ , $b+p$ , $c+p$ に変化した以外、何も変わっていません。よって平行移動で不変です。解は次のように変化します。$$P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}= P\left\{\begin{matrix}a+p & b+p & c+p\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;w\right\}$$
拡大・回転での不変性
(2.3)で $w=pz$ とすると $u'\to p\frac{du}{dw}$ , $u''\to p^2\frac{d^2u}{dw^2}$ と変化します。僅かな計算で\begin{eqnarray}&&\frac{d^2u}{dw^2}+\left(\frac{A}{w-pa}+\frac{B}{w-pb}+\frac{C}{w-pc}\right)\frac{du}{dw}\\&&\quad+\left(\frac{D(pa-pb)(pa-pc)}{w-pa}+\frac{E(pb-pa)(pb-pc)}{w-pb}+\frac{F(pc-pa)(pc-pb)}{w-pc}\right)\\&&\quad\quad\quad\times\frac{u}{(w-pa)(w-pb)(w-pc)}=0\end{eqnarray}を得て、不変であると分かります。P表記は$$P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}= P\left\{\begin{matrix}pa & pb & pc\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;w\right\}$$
反転での不変性
(2.3)で $w=1/z$ とすると$$u''\to w^4\frac{d^2u}{dw^2}+2w^3\frac{du}{dw}$$$$u'\to -w^2\frac{du}{dw}$$と変換します。ただちに\begin{eqnarray}&&w\frac{d^2u}{dw^2}+\left(2-\frac{A}{1-aw}-\frac{B}{1-bw}-\frac{C}{1-cw}\right)\frac{du}{dw}\\&&\quad+\left(\frac{D(a-b)(a-c)}{1-aw}+\frac{E(b-a)(b-c)}{1-bw}+\frac{F(c-a)(c-b)}{1-cw}\right)\\&&\quad\quad\quad\times\frac{wu}{(1-aw)(1-bw)(1-cw)}=0\end{eqnarray}のようになります。ここで第2項の $2$ を $A+B+C$ に書き換えて\begin{eqnarray}&&\frac{d^2u}{dw^2}+\left(\frac{A}{w-\frac{1}{a}}+\frac{B}{w-\frac{1}{b}}+\frac{C}{w-\frac{1}{c}}\right)\frac{du}{dw}\\&&\quad+\left(\frac{D(\frac{1}{a}-\frac{1}{b})(\frac{1}{a}-\frac{1}{c})}{w-\frac{1}{a}}+\frac{E(\frac{1}{b}-\frac{1}{a})(\frac{1}{b}-\frac{1}{c})}{w-\frac{1}{b}}+\frac{F(\frac{1}{c}-\frac{1}{a})(\frac{1}{c}-\frac{1}{b})}{w-\frac{1}{c}}\right)\\&&\quad\quad\quad\times\frac{u}{(w-\frac{1}{a})(w-\frac{1}{b})(w-\frac{1}{c})}=0\end{eqnarray}で不変です。特異点だけ移るのでP表記は$$P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}= P\left\{\begin{matrix}\frac{1}{a} & \frac{1}{b} & \frac{1}{c}\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;w\right\}$$と変化します。
任意のメビウス変換
したがって、任意のメビウス変換はこれらの変換の組み合わせで表せるのでしたから、
リーマンのP微分方程式(0.1)は任意のメビウス変換により、特異点が移ることを除いて不変である。
メビウス変換を $w=T(z)$ とすると\begin{equation}P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}= P\left\{\begin{matrix}T(a) & T(b) & T(c)\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;w\right\}\tag{2.4}\end{equation}と変化します。
$$u=P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}$$なる解のセットおよび対応する方程式があるとします。この解に\begin{equation}\left(\frac{z-a}{z-b}\right)^\mu\left(\frac{z-c}{z-b}\right)^\nu\tag{3.1}\end{equation}を掛けることを考えます。
Whittaker-Watsonによると $\left(\frac{z-a}{z-b}\right)^\mu\left(\frac{z-c}{z-b}\right)^\nu u=v$ なる変換を直接P方程式に適用することで、$v$ もまた指数が変化したP方程式の解であることが示せます(下記(3.2))。確認しようと思ったのですがかなり面倒なので、次のように簡略化して確かめましょう。
例えば $a$ まわりの級数で表される特殊解に掛けると$$\left(\frac{z-a}{z-b}\right)^\mu\left(\frac{z-c}{z-b}\right)^\nu\sum_{n=0}^\infty a_n(z-a)^{n+\a}=\frac{(z-c)^\nu}{(z-b)^{\mu+\nu}}(z-a)^{\a+\mu}\sum_{n=0}^\infty a_n(z-a)^{n}$$$\left(\frac{z-c}{z-b}\right)^\nu$ は $z=a$ で正則なのでテイラー展開できて、これと $\sum a_n(z-a)^{n}$ のコーシー積をとれば数列 $\{q_n\}$ を用いて$$\left(\frac{z-a}{z-b}\right)^\mu\left(\frac{z-c}{z-b}\right)^\nu\sum_{n=0}^\infty a_n(z-a)^{n+\a}=\sum_{n=0}^\infty q_n(z-a)^{n+\a+\mu}$$と書けます。解の指数が $\mu$ だけ変化していますね。$\a'$ でやっても同じことです。さらに $b$ , $c$ まわりの級数も同様に考えると\begin{equation}\left(\frac{z-a}{z-b}\right)^\mu\left(\frac{z-c}{z-b}\right)^\nu P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}= P\left\{\begin{matrix}a & b & c\\\a+\mu & \b-\mu-\nu & \g+\nu\\\a'+\mu & \b'-\mu-\nu & \g'+\nu\end{matrix}\;z\right\}\tag{3.2}\end{equation}を得ます。6つの指数の和が $1$ であることも満たしています。つまり元の解に(3.1)をかけたものは、新たに指数のみが変化した同じ形の解になり、それに対応する方程式の指数も変化します。
注意すべきは、特異点に無限遠点がある場合です。例えば $a=\infty$ とするとき、(3.1)では $(z-a)$ を $1$ に置き換えます。実際に $z=\infty$ まわりの級数を調べてみると、(3.2)が成り立つことが確認できます。
(3.1)を利用すると$$P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}=\left(\frac{z-a}{z-b}\right)^\a\left(\frac{z-c}{z-b}\right)^\g P\left\{\begin{matrix}a & b & c\\0 & \b+\a+\g & 0\\\a'-\a & \b'+\a+\g & \g'-\g\end{matrix}\;z\right\}$$$w=\frac{(z-a)(c-b)}{(z-b)(c-a)}$ なるメビウス変換を行うと\begin{equation}=\left(\frac{z-a}{z-b}\right)^\a\left(\frac{z-c}{z-b}\right)^\g P\left\{\begin{matrix}0 & \infty & 1\\0 & \b+\a+\g & 0\\\a'-\a & \b'+\a+\g & \g'-\g\end{matrix}\;w\right\}\tag{4.1}\end{equation}(4.1)のP表記に対応する方程式を(0.1)で書き下すと、よりシンプルな超幾何微分方程式\begin{equation}u''+\left(\frac{1+\a-\a'}{z}+\frac{1+\g-\g'}{z-1}\right)u'+\frac{(\b+\a+\g)(\b'+\a+\g)}{z(z-1)}u=0\tag{4.2}\end{equation}になります。
ということは、この超幾何微分方程式(4.2)を解けば(0.1)も解けることになります。そのため、次のようにも言えるでしょう。
確定特異点が3つのフックス型微分方程式(リーマンのP方程式)は、本質的に超幾何微分方程式のみである。
超幾何関数はリーマンのP方程式のなかで一番シンプルな形をしていますから、代表としてふさわしいです。
前回の結果と合わせると、次のようにまとめられます。
2階のフックス型微分方程式のうち、確定特異点の個数が
・1つのものは、本質的に $u''=0$ のみである。
・2つのものは、本質的にオイラー・コーシー方程式のみである。
・3つのものは、本質的に超幾何微分方程式のみである。
非常にスッキリした結論だと思います。微分方程式を解く際にも使えるので、実用的にも重要な事実です。
次回は任意のP方程式の解を超幾何関数で明示してみましょう。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。