非線型微分方程式シリーズ。前回はこちら:
1階の非線型微分方程式 - 完全微分方程式・積分因子と具体例
今回はその続きで、完全でない方程式の積分因子が簡単に見つかる稀有な例を紹介します。
$P,Q$ を同次関数(Homogeneous functions)とする。微分方程式$$P(x,y)dx+Q(x,y)dy=0$$の積分因子 $\mu$ は$$\mu=\frac{1}{xP+yQ}$$である。
これまでの流れにそって、積分因子によって完全方程式を得る方法をまず説明しますが、実践的には変数変換で簡単化する方法がありますので、そちらも紹介します。
関数 $F(x,y)$ が $n$ 次の同次性をもつとは、次を満たすことをいう。\begin{equation}F(\lambda x,\lambda y)=\lambda^nF(x,y)\tag{1}\end{equation}
これをHomogeneous functionsというのですが、調べると日本語では「斉次関数」または「同次関数」というようです。ここでは後者をとります。というのも、このあとHomogeneous differential equationなるものを扱うところで「斉次方程式」などと訳すと、こちらでとりあげたまったく別の方程式と混同してしまうからです。同じサイト内ですから、使い分けることにしました。
例えば、$F(x,y)=x^2+y^2$ や $F(x,y)=\sqrt{2x^4-y^4}$ は2次の同次関数です。なぜなら$$F(\lambda x,\lambda y)=\lambda^2F(x,y)$$であることがすぐに確かめられるからです。
(1)を $\lambda$ で偏微分すると\begin{equation}\dd{F(\lambda x,\lambda y)}{\lambda}=n\lambda^{n-1}F(x,y)\tag{2}\end{equation}となる一方で\begin{align}\dd{F(\lambda x,\lambda y)}{\lambda} &=\dd{F(\lambda x,\lambda y)}{(\lambda x)}\dd{(\lambda x)}{\lambda}+\dd{F(\lambda x,\lambda y)}{(\lambda y)}\dd{(\lambda y)}{\lambda}\\&=\dd{F(\lambda x,\lambda y)}{(\lambda x)}x+\dd{F(\lambda x,\lambda y)}{(\lambda y)}y\end{align}これらを合わせると\begin{equation}x\dd{F(\lambda x,\lambda y)}{(\lambda x)}+y\dd{F(\lambda x,\lambda y)}{(\lambda y)}=n\lambda^{n-1}F(x,y)\tag{3}\end{equation}$\lambda =1$ として次を得ます。
$n$ 次の同次関数 $F$ について$$n F(x,y)=x\dd{F(x,y)}{x}+y\dd{F(x,y)}{y}$$
1階微分方程式を次の形で表したとします。\begin{equation}P(x,y)dx+Q(x,y)dy=0\tag{4}\end{equation}前回の復習をすると
\begin{equation}\dd{P}{y}=\dd{Q}{x}\tag{5}\end{equation}が成り立つとき、$$P(x,y)dx+Q(x,y)dy=0$$は完全微分方程式である。
完全であれば、即座に積分計算で解いていくことができるのですが、$P,Q$ が完全でない場合、$\mu(x,y)$ をかけて $\mu P$ , $\mu Q$ が完全になるようにします(そうなるような $\mu$ を見つける必要がある)。すると\begin{equation}\mu(x,y)P(x,y)dx+\mu(x,y)Q(x,y)dy=0\tag{6}\end{equation}が完全微分方程式になります。すなわち\begin{equation}\dd{\mu P}{y}=\dd{\mu Q}{x}\tag{7}\end{equation}です。このような $\mu$ を積分因子といいます。
本題に入ります。方程式\begin{equation}P(x,y)dx+Q(x,y)dy=0\tag{8}\end{equation}において $P,Q$ がともに $n$ 次の同次関数であるとします。(8)が完全でないとき、\begin{equation}\mu=\frac{1}{xP+yQ}\tag{9}\end{equation}と定義します。
このとき\begin{equation}\dd{\mu}{y}=-\mu^2\left( Q+x\dd{P}{y}+y\dd{Q}{y}\right)\tag{10}\end{equation}であることから\begin{align}\dd{\mu P}{y} &=\dd{}{y}\frac{P}{xP+yQ}\\&=\mu\dd{P}{y}-\mu^2P\left(Q+x\dd{P}{y}+y\dd{Q}{y}\right)\end{align}同様に\begin{align}\dd{\mu Q}{x} =\mu\dd{Q}{x}-\mu^2Q\left(P+x\dd{P}{x}+y\dd{Q}{x}\right)\end{align}これらを引き算しましょう。\begin{align}\dd{\mu P}{y}-\dd{\mu Q}{x} &=\mu\left[\dd{P}{y}-\dd{Q}{x}-\mu P\left(x\dd{P}{y}+y\dd{Q}{y}\right)+\mu Q\left(x\dd{P}{x}+y\dd{Q}{x}\right)\right]\end{align}$y\dd{Q}{y}$ , $x\dd{P}{x}$ に定理2を適用すると、$nPQ$ が相殺して\begin{align}\dd{\mu P}{y}-\dd{\mu Q}{x} &=\mu\left[\dd{P}{y}-\dd{Q}{x}+\mu\left\{\dd{Q}{x}(\underbrace{xP+yQ}_{=1/\mu})-\dd{P}{y}(\underbrace{xP+yQ}_{=1/\mu})\right\}\right]\\ &=0\end{align}\begin{equation}\therefore\quad\dd{\mu P}{y}=\dd{\mu Q}{x}\tag{11}\end{equation}したがって(9)で定義した $\mu$ は積分因子です。よって同次形微分方程式では積分因子を機械的に設定できて、(そのあとの積分ができるなら)解くことができます。
上で説明した方法では、実際には積分因子をかけたあとの計算が面倒になるかもしれません。同次形微分方程式については、以下のような変数変換による有名な解法がありますので紹介します。
$y=vx$ とすると\begin{equation}dy=xdv+vdx\tag{12}\end{equation}となります。
補足:$y(x)=v(x)x$ を $x$ で微分すると$$\frac{dy}{dx}=v+x\frac{dv}{dx}$$
(12)を同次形微分方程式 $Pdx+Qdy=0$ に用いると、$y$ を消去していって\begin{align}0&=P(x,xv)dx+Q(x,xv)(xdv+vdx)\\&=x^nP(1,v)dx+x^nQ(1,v)(xdv+vdx)\\&=\{P(1,v)+vQ(1,v)\}dx+xQ(1,v)dv\end{align}変数分離により\begin{equation}\frac{dx}{x}=-\frac{Q(1,v)}{P(1,v)+vQ(1,v)}dv\tag{13}\end{equation}\begin{equation}\therefore\quad \ln cx=-\int\frac{Q(1,v)}{P(1,v)+vQ(1,v)}dv\tag{14}\end{equation}として解くことができます。
要は $y=vx$ として変数分離する。それだけです。
$$2xy^3 y'=4x^4-x^2y^2+2y^4$$
【解答】$y=vx$ とおくと $y'=v+xv'$ なので$$2v^3xv'=4-v^2$$変数分離により$$\frac{dx}{2x}=\frac{v^3}{4-v^2}dv$$積分して$$\ln cx=-\frac{y^2}{x^2}-4\ln\left(\frac{y^2}{x^2}-4\right)$$
$$y'=\frac{2xy}{x^2+y^2}$$
【解答】$y=vx$ とおくと$$xv'=\frac{v-v^3}{1+v^2}$$変数分離により$$\frac{dx}{x}=\frac{1+v^2}{v-v^3}dv$$積分して$$\ln cx=\ln\frac{v}{1-v^2}$$$$\therefore\quad \frac{y}{x^2-y^2}=c$$と求まります。2次曲線です。
$$y'=\frac{2x^2+y^2}{3y^2-2xy}$$
【解答】$y=vx$ とおくと$$xv'=\frac{-3v^3+3v^2+2}{3v^2-2v}$$変数分離により$$-3\frac{dx}{x}=\frac{9v^2-6v}{3v^3-3v^2-2}dv$$積分して$$-3\ln ax=\ln(3v^3-3v^2-2)$$定数 $a$ をとりなおして$$2x^3+3xy^2-3y^3=c$$と求まります。
$$x\left(\frac{dy}{dx}\right)^2-2y\left(\frac{dy}{dx}\right)+x=0$$
【解答】$t=-x$ とすると$$t\left(\frac{dy}{dt}\right)^2-2y\left(\frac{dy}{dt}\right)+t=0$$で方程式の形は不変。つまり $y(x)=y(t)=y(-x)$ より、解は $y$ 軸対称だと分かるため、$x\ge 0$ に限定して考える。また $z(x)=-y(x)$ なる変換でも方程式の形は不変なので、解は $x$ 軸対称だと分かるため、$y\ge0$ に限定する。
与方程式は $y'$ の2次方程式の形をしており、$$y'=\frac{y\pm \sqrt{y^2-x^2}}{x}$$で同次形微分方程式になっている。解は $y^2-x^2\ge 0$ の範囲にあることになるが、今は第1象限に絞っているので $y\ge x\ge0$ である。
$y=vx$ とおくと$$\frac{dv}{\sqrt{v^2-1}}=\pm \frac{dx}{x}$$$v\ge 1$ なので$$\ln(v+\sqrt{v^2-1})=\pm \ln cx$$対数をはずすと$$v+\sqrt{v^2-1}=\begin{cases}cx\\\dfrac{1}{cx}\end{cases}$$$v$ を $y$ に戻して$$y+\sqrt{y^2-x^2}=\begin{cases}cx^2\\\dfrac{1}{c}\end{cases}$$式が上下2つに分かれているが、左辺の $y$ を右辺に移項して両辺を2乗すると、どちらも同じ式となり、$$c^2x^2-2cy+1=0$$という放物線になる。
第1象限のみを考えてきたが、この放物線の式は $x\to-x$ としても成り立ち、$c$ の任意性から $y\to -y$ としたときも含んでいる。よってこの式が一般解となる。
【補足:特異解について】
例4の方程式の一般解は$$c^2x^2-2cy+1=0$$でしたが、実はもう1つの解があります。一般解の放物線は $x=\pm 1/c$ において直線 $y=\pm x$ と接します。
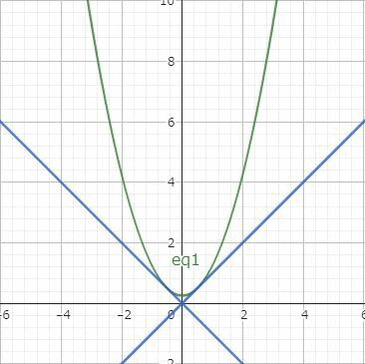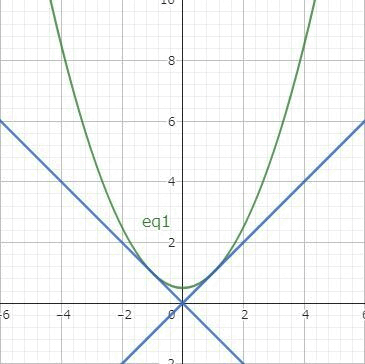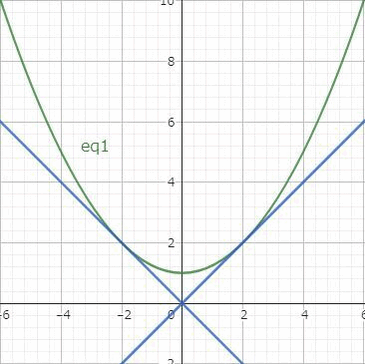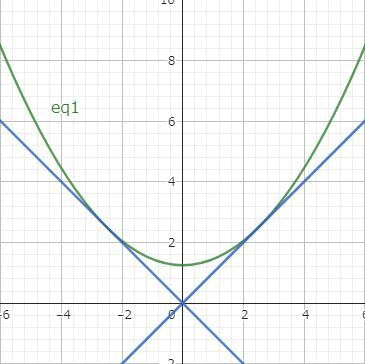
そこで $y=\pm x$ をもとの微分方程式に代入してみると、確かに解になっています。これは一般解であらわすことができないので特異解とよびます。
このような例はクレローの方程式等でもみられます。参考にリンクを貼っておきます。
次はこちら:
y'=(Ax+By+E)/(Cx+Dy+F)の形の微分方程式
ほかの微分方程式の記事:
[1] H.T.Davis (1960), Introduction to nonlinear differential and integral equations, U.S. Atomic Energy Commission [2] Wikipedia contributors. (2024, May 8). Homogeneous function. In Wikipedia, The Free Encyclopedia. Retrieved May 24, 2024
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
