これまでの $log$ を含む難しい積分シリーズはこちら:
$a\ge 0$ , $c\ge b^2$ とするとき、次の等式を証明する。\begin{eqnarray*}I(a,b,c) &:=& \int_0^\infty \frac{x}{x^2+a^2}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx \\ &=& 2\pi\arctan\frac{b}{a+\sqrt{c-b^2}}\end{eqnarray*}特に $a=0$ のときは次のようにも書ける。$$ \int_0^\infty \frac{1}{x}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx = 2\pi \arcsin\frac{b}{\sqrt{c}}$$
具体的な積分値は\begin{eqnarray*}\int_0^\infty \frac{1}{x}\ln\frac{x^2+2x+2}{x^2-2x+2}dx &=& \frac{\pi^2}{2} \\ \int_0^\infty \frac{1}{x}\ln\frac{x^2+2x+4}{x^2-2x+4}dx &=& \frac{\pi^2}{3} \\ \int_0^\infty \frac{1}{x}\ln\frac{x^2+2\sqrt{3}x+4}{x^2-2\sqrt{3}x+4}dx &=& \frac{2\pi^2}{3}\end{eqnarray*}
\begin{eqnarray*}\int_0^\infty \frac{x}{x^2+1}\ln\frac{x^2+2\sqrt{3}x+7}{x^2-2\sqrt{3}x+7}dx &=& \frac{\pi^2}{3} \\\int_0^\infty \frac{x}{x^2+1}\ln\frac{x^2+2x+3}{x^2-2x+3}dx &=& \frac{\pi^2}{4} \\\int_0^\infty \frac{x}{x^2+1}\ln\frac{x^2+2(\sqrt{2}+1)x+4\sqrt{2}+7}{x^2-2(\sqrt{2}+1)x+4\sqrt{2}+7}dx &=& \frac{3\pi^2}{8} \\\int_0^\infty \frac{x}{x^2+1}\ln\frac{x^2+2(2-\sqrt{3})x+15-8\sqrt{3}}{x^2-2(2-\sqrt{3})x+15-8\sqrt{3}}dx &=& \frac{\pi^2}{12} \\\int_0^\infty \frac{x}{x^2+2}\ln\frac{x^2+4x+12}{x^2-4x+12}dx &=& \frac{\pi^2}{4}\end{eqnarray*}
上2つの式はYury Brychkov, "Handbook of Special Functions: Derivatives, Integrals, Series and Other Formulas" において記された積分です。なお本書ではこの式が間違っており(誤植が多すぎる!)、本記事では訂正済みです。当ブログではこの本に書かれた積分を証明する記事を多数書いておりますが、高確率で致命的な誤植に出会います。なので自分でウラをとらない限り、気軽に参照できません。では見ていきましょう。
書籍はAmazon等で買えます。700ページもあり、非常に多くの微分・積分・級数公式が網羅されています。眺めるだけでも面白いです。

Handbook of Special Functions: Derivatives, Integrals, Series and Other Formulas
式の変形
$a\ge 0$ , $c\ge b^2$ として、本日扱う積分を次のように定義します。\begin{equation}I(a,b,c) := \int_0^\infty \frac{x}{x^2+a^2}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx\tag{1}\end{equation}
まずは $a=0$ に限ったケースでやります。つまり\begin{equation}I(0,b,c) =\int_0^\infty \frac{1}{x}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx\tag{2}\end{equation}形からして複素解析によって求まりそうです。被積分関数は偶関数(even function)なので$$I(0,b,c)=\frac{1}{2}\int_{-\infty}^\infty \frac{1}{x}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx$$$\log$ の中が大変複雑ですので、いったん部分積分をして\begin{eqnarray*}I(0,b,c) &=&\frac{1}{2}\left[\ln x\ln\frac{x^2+2bx+c}{x^2-2bx+c}\right]_{-\infty}^\infty-\int_{-\infty}^\infty \left(\frac{x+b}{x^2+2bx+c}-\frac{x-b}{x^2-2bx+c}\right)\ln x dx \\&=& -\int_{-\infty}^\infty \left(\frac{x+b}{x^2+2bx+c}-\frac{x-b}{x^2-2bx+c}\right)\ln x dx\end{eqnarray*}したがって\begin{equation}I(0,b,c) = 2b\int_{-\infty}^\infty\frac{(x^2-c)\ln x}{(x^2+2bx+c)(x^2-2bx+c)}dx\tag{3}\end{equation}
条件 $c\ge b^2$ によって(3)の極はすべて虚数であり、$\a,\b,\g,\delta$ とすると\begin{equation}I(0,b,c) = 2b\int_{-\infty}^\infty\frac{(x^2-c)\ln x}{(x-\a)(x-\b)(x-\g)(x-\d)}dx\tag{4}\end{equation} ただし\begin{eqnarray}\a=-b+i\sqrt{c-b^2}\quad,\quad \b=-b-i\sqrt{c-b^2} \\ \g=b+i\sqrt{c-b^2}\quad,\quad \d=b-i\sqrt{c-b^2}\tag{5}\end{eqnarray}いま $b>0$ としておきましょう。(3)からして、$b$ の符号が入れ替わると積分値の符号も入れ替わります。とりあえず $b>0$ としておいて、最後にそれが確認できればよいです。
留数定理で解く
さて、ここで次の複素関数を定義します。\begin{equation}f(z):=\frac{(z^2-c)\ln z}{(z-\a)(z-\b)(z-\g)(z-\d)}\tag{6}\end{equation}また周回経路 $C$を下図のようにとります。
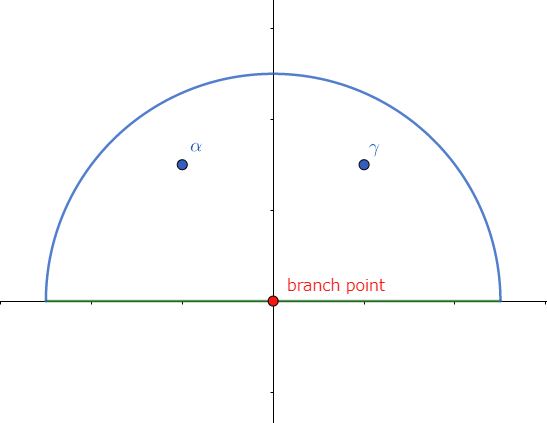
$f(z)$ は $\ln z$ をもつため、原点に分岐点(branch point)をもち、$[0,-i\infty)$ に切断(branch cut)があります。なので上図に反して、実際は原点を小半円で避けることになりますが、$z=\epsilon e^{i\t}$ とおくと $\epsilon\to0$ で積分値は $O(\epsilon \ln\epsilon)$ となるのでゼロと評価されます。なので上図では小半円を省いています。また大円についても $z=Re^{i\t}$ と置換して $R\to\infty$ とすれば積分値はゼロとなります。したがって\begin{equation}\oint_C f(z)dz = \int_{-\infty}^\infty f(x)dx\tag{7}\end{equation}と表されます。
留数定理(residue theorem)によって周回積分を計算しましょう。経路図より上半円内に1位の極(pole)は $z=\a,\g$ の2つです。したがって、やや面倒な計算をして\begin{eqnarray*}\oint_C f(z)dz &=& 2\pi i\left[\left.\frac{(z^2-c)\ln z}{(z-\b)(z-\g)(z-\d)}\right|_{z=\a}+\left.\frac{(z^2-c)\ln z}{(z-\a)(z-\b)(z-\d)}\right|_{z=\g}\right] \\&=& \frac{i\pi}{2b}\ln\frac{\g}{\a} \\&=& \frac{i\pi}{b}\ln\left(\sqrt{1-\frac{b^2}{c}}-\frac{b}{\sqrt{c}}i\right)\end{eqnarray*}この $\ln$ の中身は、絶対値 $1$ で偏角 $-\arcsin \frac{b}{\sqrt{c}}$ となっていますので$$\oint_C f(z)dz=\frac{\pi}{b}\arcsin \frac{b}{\sqrt{c}}$$(7)より$$\int_{-\infty}^\infty f(x)dx=\frac{\pi}{b}\arcsin \frac{b}{\sqrt{c}}$$$f(z)$ の定義(6)と(4)により次の結論を得ます。
\begin{eqnarray}I(0,b,c) &=& \int_0^\infty \frac{1}{x}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx \\&=& 2\pi \arcsin\frac{b}{\sqrt{c}}\tag{8}\end{eqnarray}
$b$ を $-b$ に変えても成立するので、$b<0$ でもOKとなります。
ではより一般的な場合 $a>0$ について考えましょう。複素解析を用いる点では先ほどと同じですが、分岐点をより意識した積分が必要になります。
式の変形
積分を再掲しておきます。$a,b>0$ , $c\ge b^2$ として\begin{equation}I(a,b,c) := \int_0^\infty \frac{x}{x^2+a^2}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx\tag{9}\end{equation}やはり偶関数ですので$$I(a,b,c)=\frac{1}{2}\int_{-\infty}^\infty \frac{x}{x^2+a^2}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx$$先ほどと同様に部分積分します。$$I(a,b,c)=-\frac{1}{2}\int_{-\infty}^\infty\left(\frac{x+b}{x^2+2bx+c}-\frac{x-b}{x^2-2bx+c}\right)\ln (x^2+a^2) dx$$式を整理すると\begin{equation}I(a,b,c)=b\int_{-\infty}^\infty\frac{(x^2-c)\ln(x^2+a^2)}{(x^2+2bx+c)(x^2-2bx+c)}dx\tag{10}\end{equation}分母を虚数で無理やり因数分解すると\begin{equation}I(a,b,c) = b\int_{-\infty}^\infty\frac{(x^2-c)\ln (x^2+a^2)}{(x-\a)(x-\b)(x-\g)(x-\d)}dx\tag{11}\end{equation} ただし\begin{eqnarray}\a=-b+i\sqrt{c-b^2}\quad,\quad \b=-b-i\sqrt{c-b^2} \\ \g=b+i\sqrt{c-b^2}\quad,\quad \d=b-i\sqrt{c-b^2}\tag{12}\end{eqnarray}
周回積分の計算(留数定理)
ここで次の複素関数を定義します。\begin{equation}f(z):=\frac{(z^2-c)\ln(z^2+a^2)}{(z-\a)(z-\b)(z-\g)(z-\d)}\tag{13}\end{equation}また周回経路 $C$を下図のようにとります。
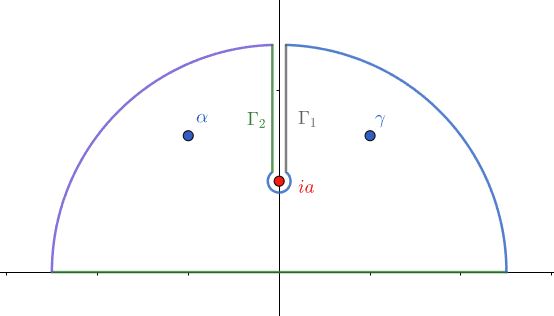
$f(z)$ は $\ln(z^2+a^2)$ をもつために、$z=\pm ia$ が分岐点(branch point)となっており、切断(branch cut)は $[ia,i\infty)$ および $(-i\infty,-ia]$ の2本ですが、今は上半平面のみ考えればよいです。また $f(z)$ は上半平面内に1位の極(pole) $z=\a,\g$ をもちます。
周回積分を考えましょう。2つの大円弧での積分は先ほどと同様にゼロ。分岐点 $ia$ まわりの小円も、先ほどの原点回りの小円と同じように評価するとゼロ。よって\begin{equation}\oint_C f(z)dz = \int_{-\infty}^\infty f(x)dx+\int_{\G_1} f(z)dz+\int_{\G_2}f(z)dz\tag{14}\end{equation}
まずは左辺の周回積分を留数定理により求めます。計算に役立つよう、先にいくつか値を示しておきます。\begin{eqnarray}\a^2 &=& 2b^2-c-2bi\sqrt{c-b^2}\\\g^2 &=& 2b^2-c+2bi\sqrt{c-b^2}\tag{15}\end{eqnarray}\begin{eqnarray}\a-\b &=& 2i\sqrt{c-b^2} \\ \a-\g &=& -2b \\ \a-\d &=& -2b+2i\sqrt{c-b^2} \\ \g-\b &=& 2b+2i\sqrt{c-b^2} \\ \g-\d &=& 2i\sqrt{c-b^2}\tag{16}\end{eqnarray}\begin{equation}\frac{\g^2+a^2}{\a^2+a^2}=e^{2i\t}\quad,\;\tan\t=\frac{2b\sqrt{c-b^2}}{a^2+2b^2-c}\tag{17}\end{equation}
これらを用いて留数(residue)を計算すると\begin{equation}\oint_Cf(z)dz=-\frac{\pi}{b}\arctan\frac{2b\sqrt{c-b^2}}{a^2+2b^2-c}\tag{18}\end{equation}
切断に沿った積分
残りの $\G_1$ と $\G_2$ の積分を計算します。$f(z)$ を少し変形すると$$f(z)=\frac{(z^2-c)\ln\bigl((z+ia)(z-ia)\bigr)}{(z+2bz+c)(z-2bz+c)}$$問題となるのは $\ln(z-ia)$ です。切断が正の虚軸に入っていることから、偏角を $-\frac{3}{2}\pi<\arg(z-ia)<\frac{\pi}{2}$ とします。
$\G_1$ においては $z=ia+xe^{i\frac{\pi}{2}}$ と置換して $x=\infty$ から $0$ まで変化させます。$\ln(z-ia)=\ln x+i\frac{\pi}{2}$ となり、ほかの $z$ へは $z=i(x+a)$ を代入すればOKです。
$\G_2$ においては $z=ia+xe^{-i\frac{3\pi}{2}}$ と置換して $x=0$ から $\infty$ まで変化させます。$\ln(z-ia)=\ln x-i\frac{3\pi}{2}$ となり、ほかの $z$ へは $z=i(x+a)$ を代入すればOKです。\begin{eqnarray*}&&\int_{\G_1} f(z)dz+\int_{\G_2}f(z)dz \\&=& \int_\infty^0\frac{(-(x+a)^2-c)\ln\left(i(x+2a)xe^{i\frac{\pi}{2}}\right)}{[-(x+a)^2-2ib(x+a)+c][-(x+a)^2+2ib(x+a)+c]}idx \\&&+ \int_0^\infty\frac{(-(x+a)^2-c)\ln\left(i(x+2a)xe^{-i\frac{3\pi}{2}}\right)}{[-(x+a)^2-2ib(x+a)+c][-(x+a)^2+2ib(x+a)+c]}idx \\&=& i\int_0^\infty\frac{-((x+a)^2+c)\cdot(-2\pi i)}{[(x+a)^2+2ib(x+a)-c][(x+a)^2-2ib(x+a)-c]}dx \\&=& -2\pi\int_0^\infty\frac{(x+a)^2+c}{[(x+a)^2+2ib(x+a)-c][(x+a)^2-2ib(x+a)-c]}dx \\&=& -2\pi\int_a^\infty\frac{x^2+c}{(x^2+2ibx-c)(x^2-2ibx-c)}dx \\&=& \frac{i\pi}{2b}\int_a^\infty\left(\frac{2x-2ib}{x^2-2ibx-c}-\frac{2x+2ib}{x^2+2ibx-c}\right)dx \\&=& \frac{i\pi}{2b}\left[\ln\frac{x^2-2ibx-c}{x^2+2ibx-c}\right]_a^\infty \\&=& \frac{i\pi}{2b}\ln\frac{a^2+2iab-c}{a^2-2iab-c} \\&=& \frac{i\pi}{2b}\ln e^{2i\phi}\quad,\;\tan\phi=\frac{2ab}{a^2-c}\end{eqnarray*}以上より\begin{equation}\int_{\G_1} f(z)dz+\int_{\G_2}f(z)dz=-\frac{\pi}{b}\arctan\frac{2ab}{a^2-c}\tag{19}\end{equation}これに(14)(18)とあわせて$$-\frac{\pi}{b}\arctan\frac{2b\sqrt{c-b^2}}{a^2+2b^2-c} = \int_{-\infty}^\infty f(x)dx-\frac{\pi}{b}\arctan\frac{2ab}{a^2-c}$$$$\therefore\quad \int_{-\infty}^\infty f(x)dx=\frac{\pi}{b}\left(\arctan\frac{2ab}{a^2-c}-\arctan\frac{2b\sqrt{c-b^2}}{a^2+2b^2-c}\right)$$
式の整理
メインとなる計算は終わりましたが、ここからの計算が案外厄介です。最後に得た結果は$$\int_{-\infty}^\infty f(x)dx=\frac{\pi}{b}\left(\phi-\t\right)\quad,\;\tan\phi=\frac{2ab}{a^2-c}\;,\;\tan\t=\frac{2b\sqrt{c-b^2}}{a^2+2b^2-c}$$となります。$f(x)$ の定義を思い出すと(11)より$$I(a,b,c)=\pi(\phi-\t)$$したがって\begin{equation}I(a,b,c)=2\pi\cdot\frac{\phi-\t}{2}\tag{20}\end{equation}半角の公式$$\tan^2 \frac{x}{2}=\frac{1-\cos x}{1+\cos x}$$を用いて計算すると\begin{eqnarray}\tan\frac{\phi}{2}&=&\frac{\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2}{2ab} \\\tan\frac{\t}{2}&=&\frac{\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2-2b^2}{2b\sqrt{c-b^2}}\tag{21}\end{eqnarray}加法定理より\begin{eqnarray*}\tan\frac{\phi-\t}{2}&=&\frac{\tan\frac{\phi}{2}-\tan\frac{\t}{2}}{1+\tan\frac{\phi}{2}\tan\frac{\t}{2}} \\&=& \frac{2b\sqrt{c-b^2}\left[\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2\right]-2ab\left[\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2-2b^2\right]}{4ab^2\sqrt{c-b^2}+\left[\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2\right]\left[\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2-2b^2\right]} \\&=& 2b\frac{(\sqrt{c-b^2}-a)\left[\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2\right]+2ab^2}{4ab^2\sqrt{c-b^2}+2(a^2-c)^2+4a^2b^2+2(c-a^2)\sqrt{(a^2-c)^2+4a^2b^2}-2b^2\left[\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2\right]} \\&=& b\frac{(\sqrt{c-b^2}-a)\left[\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2\right]+2ab^2}{2ab^2(\sqrt{c-b^2}+a)+(c-b^2-a^2)\left[\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2\right]} \\&=& b\frac{2ab^2+(\sqrt{c-b^2}-a)\left(\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2\right)}{(\sqrt{c-b^2}+a)\left[2ab^2+(\sqrt{c-b^2}-a)\left(\sqrt{(a^2-c)^2+4a^2b^2}+c-a^2\right)\right]} \\&=& \frac{b}{\sqrt{c-b^2}+a}\end{eqnarray*}$$\therefore\quad\frac{\phi-\t}{2}=\arctan\frac{b}{\sqrt{c-b^2}+a}$$以上より次の結論を得ます。
\begin{eqnarray}I(a,b,c) &:=& \int_0^\infty \frac{x}{x^2+a^2}\ln\frac{x^2+2bx+c}{x^2-2bx+c}dx \\ &=& 2\pi\arctan\frac{b}{a+\sqrt{c-b^2}}\tag{22}\end{eqnarray}
$a,b,c$ に好きな値を代入して、具体的な積分値が得られます。$a=0$ の場合は(8)を用いて
\begin{eqnarray*}\int_0^\infty \frac{1}{x}\ln\frac{x^2+2x+2}{x^2-2x+2}dx &=& \frac{\pi^2}{2} \\ \int_0^\infty \frac{1}{x}\ln\frac{x^2+2x+4}{x^2-2x+4}dx &=& \frac{\pi^2}{3} \\ \int_0^\infty \frac{1}{x}\ln\frac{x^2+2\sqrt{3}x+4}{x^2-2\sqrt{3}x+4}dx &=& \frac{2\pi^2}{3}\end{eqnarray*}
$a>0$ では(22)を用います。この際$$\arctan x=2\arctan\left(\frac{x}{1+\sqrt{1+x^2}}\right)$$を利用することもできます。
\begin{eqnarray*}\int_0^\infty \frac{x}{x^2+1}\ln\frac{x^2+2\sqrt{3}x+7}{x^2-2\sqrt{3}x+7}dx &=& \frac{\pi^2}{3} \\\int_0^\infty \frac{x}{x^2+1}\ln\frac{x^2+2x+3}{x^2-2x+3}dx &=& \frac{\pi^2}{4} \\\int_0^\infty \frac{x}{x^2+1}\ln\frac{x^2+2(\sqrt{2}+1)x+4\sqrt{2}+7}{x^2-2(\sqrt{2}+1)x+4\sqrt{2}+7}dx &=& \frac{3\pi^2}{8} \\\int_0^\infty \frac{x}{x^2+1}\ln\frac{x^2+2(2-\sqrt{3})x+15-8\sqrt{3}}{x^2-2(2-\sqrt{3})x+15-8\sqrt{3}}dx &=& \frac{\pi^2}{12} \\\int_0^\infty \frac{x}{x^2+2}\ln\frac{x^2+4x+12}{x^2-4x+12}dx &=& \frac{\pi^2}{4}\end{eqnarray*}
次
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。



