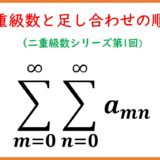
二重級数シリーズ第2回。前回は、一般に二重級数の極限は逐次極限(1つずつ極限をとること)と一致しないことを取り上げました。また二重級数の和の順番(タテかヨコか正方形か対角線か)によっても極限値が変わってしまうことも示しました。
しかし実際の計算上、これではあまりにデリケートで不便です。そこで目指すべきは、どのような条件の数列だったら順序に融通が利くのかということでしょう。その第一歩としてすべての項 $a_{mn}$ が非負である正項二重級数を考えます。
正項級数の特徴は、$a_{mn}\ge 0$ であるため、$\{S_{mn}\}$ が $m$ についても $n$ についても広義単調増加であるということです。これによって順序が自由になります。
前回の記事で「正方形並べ」という和の取り方を紹介しました。\begin{equation}\begin{matrix}a_{0,0} & & a_{0,1} & & a_{0,2}\\&&\downarrow&&\downarrow\\ a_{1,0} & \leftarrow& a_{1,1} & & a_{1,2}\\ & & & &\downarrow\\ a_{2,0} &\leftarrow & a_{2,1} &\leftarrow & a_{2,2}\end{matrix}\tag{1}\end{equation}のような順に足します。すなわち \begin{equation}S_{mm}=a_{0,0}+(a_{0,1}+a_{1,1}+a_{1,0})+(a_{0,2}+a_{1,2}+a_{2,2}+a_{2,1}+a_{2,0})+\cdots\tag{2}\end{equation}群数列のようなイメージで、$m$ 群までとった部分和は $S_{mm}$ となります。実は面白いことに、次が成り立つのです。
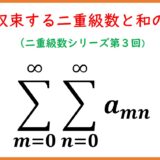
正項の二重級数 $\sum a_{mn}$ すなわち二重数列 $\{S_{mn}\}$ が収束する必要十分条件は $\{S_{mm}\}$ が収束することであり、両者は同じ極限をもつ。
【証明】二重数列の収束については前回記事を参照。定義1.1を適用すると、$\{S_{mn}\}$ が収束するならば特に $m=n\ge N$ としてもよい。よって $\{S_{mm}\}$ は収束する。
次に $\{S_{mm}\}$ が収束するならば、$$\forall\epsilon>0,\;\exists N\in\NN,\;\forall m\ge N,\;|S_{mm}-S|<\epsilon$$である。さらに $\{S_{mn}\}$ は $m$ , $n$ について単調増加だから $S-\epsilon<S_{NN}\le S$ であり、$\forall m,n\ge N$ に対して$$S-\epsilon<S_{NN}\le S_{mn}\le S\Rightarrow|S_{mn}-S|<\epsilon$$【証明終】
一般に二重級数の極限と逐次極限は一致しないことを前回解説しました。ところが正項級数の場合は、ありがたいことに以下が成り立ちます。
正項の二重級数 $\sum a_{mn}$ と、その逐次極限すなわち$$\lim_{m,n\to\infty} S_{mn}\;,\;\lim_{m\to\infty}\left(\lim_{n\to\infty} S_{mn}\right)\;,\;\lim_{n\to\infty}\left(\lim_{m\to\infty} S_{mn}\right)$$書き換えると$$\sum_{m,n=0}^\infty a_{mn}\;,\;\sum_{m=0}^\infty\left(\sum_{n=0}^\infty a_{mn}\right)\;,\;\sum_{n=0}^\infty\left(\sum_{m=0}^\infty a_{mn}\right)$$のいずれかが収束するならば残りの2つも収束し、極限は(発散も含め)一致する。
【証明】二重級数が $S$ に収束する場合、単調増加性から $S_{mn}\le S$ であるので、上に有界であり$$\forall\epsilon>0,\;\exists N,\;\forall m,n\ge N,\;S-\epsilon<S_{mn}\le S$$$m\ge N$ を固定して $n$ で無限和をとるとき、やはり $S$ を超えない。よって $\displaystyle\lim_{n\to\infty} S_{mn}$ が存在して $S$ 以下の極限値をとる。すなわち$$\forall m\ge N,\;S-\epsilon<\lim_{n\to\infty} S_{mn}\le S$$$$\therefore\quad\lim_{m\to\infty}\left(\lim_{n\to\infty} S_{mn}\right)=S$$同様に$$\lim_{n\to\infty}\left(\lim_{m\to\infty} S_{mn}\right)=S$$
逆に $\displaystyle\lim_{m\to\infty}\left(\lim_{n\to\infty} S_{mn}\right)=S$ なら 単調増加性から $$S_{mm}\le \lim_{n\to\infty}S_{mn}\le S$$$S_{mm}$ が単調増加かつ上に有界となるため収束するが、同時に定理7.1により $S_{mn}$ が二重級数として収束する。さらに前半の議論からその値は $\displaystyle\lim_{m\to\infty}\left(\lim_{n\to\infty} S_{mn}\right)$ と同じで $S$ のはずである。$\displaystyle\lim_{n\to\infty}\left(\lim_{m\to\infty} S_{mn}\right)$ も然り。
最後に、3つの級数はいずれも収束するか無限大に発散するかのどちらかである。よって発散も含めて一致する。【証明終】
これによって二重級数あるいは逐次極限の計算方法にかなりの自由度が生まれます。各項が非負であればいいという単純な前提なのがうれしいです。
二重級数を1つ1つ実際に足し上げるには、結局は級数を1列に並べて足すことになります(逐次極限は足し上げる途中で極限をとっているので話が異なる)。その順番を任意に変えるとどうなるのでしょうか。
正項の二重級数 $\sum a_{mn}=S$ の順序を変更しても、和は $S$ である。
【証明】$$S_{mn}=a_{0,0}+a_{0,1}+\cdots+a_{0,n}+a_{1,0}+a_{1,1}+\cdots+a_{m,n}$$は $m,n$ について広義単調増加なので$$\forall m,n\in\NN\;,\; S_{mn}\le S$$$S_{mn}$ を並べ替えたものを$$S'_{mn}=a'_{0,0}+a'_{0,1}+\cdots+a'_{0,n}+a'_{1,0}+a'_{1,1}+\cdots+a'_{m,n}$$とする。これらの項のうち左側の添え字が最大のもの $a_{M\bullet}$ および右側の添え字が最大のもの $a_{\bullet N}$ があります。明らかに$$S'_{mn}\le S_{MN}<S$$$S'_{mn}$ は広義単調増加で上に有界なので極限 $S'$ があって $S'\le S$ となる。逆のことをすると $S\le S'$ を得るので$$S=S'$$【証明終】
直感的にも分かることではありますが、
$a_{mn}\ge 0$ に対して二重級数 $\sum a_{mn}$ が収束することの必要十分条件は$$\left\{\left.\sum_{k=0}^m\sum_{l=0}^n a_{kl}\right|m,n\in\NN\right\}$$が有界であることである。そして二重級数の極限はこの集合の上限である。
【証明】二重級数が収束する場合、収束の定義1.1 を援用すればよい。このとき $\displaystyle\sum_{k=0}^N\displaystyle\sum_{l=0}^N a_{kl}$ までは有限個の列なので有界であり、それより先 $m,n\ge N$ においても $S-\epsilon<S_{mn}<S+\epsilon$ なので有界である。
次に上記の集合すなわち $\{S_{mn}\}$ が有界とすると、 $m,n$ について単調増加であるので収束する。よって必要十分性が示された。
また $S_{mn}\le S$ なので $S$ は $\{ S_{mn}\}$ の上界であり、$S_{mn}+\epsilon>S$ なので $S$ は上限である。 【証明終】
すべて正項であることを前提に話を進めてきましたが、有限個の負項も許して議論が可能です。というのも、有限個であるということは、最後に現れる負項が存在します。よって、ある自然数 $N$ が存在して $\forall n\ge N$ では、結局、正項の列となります。$N$ までは有限和なので収束していますから、級数全体としても収束が言えます。
以上、正項(非負項)の二重級数は逐次極限をはじめ、並べ方を変えても問題ないことが確認できました。では、このようなことが可能なのは正項のときだけなのでしょうか?そこで現れるのが絶対収束という概念です。正項でなくとも絶対収束であれば、級数の順番を変えることができます。次回で見ていきましょう。
前回記事で書ききれなかった例題および今回の知見を応用した例題を掲載します。
$a_{mn}=\dfrac{(-1)^{m+n}}{2^{m+n}}\displaystyle\binom{m}{n}$ について、逐次極限と正方形並べでの極限を求めよ。ただし二項係数 $\binom{m}{n}$ において $m<n$ ではゼロと定義する。
因みに一般の二項係数はポッホハマー記号を用いて$$\binom{m}{n}=\frac{(-1)^n(-m)_n}{n!}$$と押さえておくとよい。$$\sum_{n=0}^\infty a_{mn} =\left(-\frac{1}{2}\right)^m\sum_{n=0}^m \frac{(-1)^{n}}{2^{n}}\displaystyle\binom{m}{n}=\left(-\frac{1}{4}\right)^m$$かたや\begin{eqnarray*}\sum_{m=0}^\infty a_{mn} &=&\left(-\frac{1}{2}\right)^n\sum_{m=n}^\infty \frac{(-1)^{m}}{2^{m}}\displaystyle\binom{m}{n}\\&=& \left(-\frac{1}{2}\right)^{2n}\sum_{m=0}^\infty \frac{(-1)^{m}}{2^{m}}\displaystyle\binom{m+n}{n} \\&=& \frac{1}{4^n}\sum_{m=0}^\infty\frac{(n+1)_m}{m!}\left(-\frac{1}{2}\right)^m\\&=& \frac{1}{4^n}\left.\frac{1}{(1-x)^{n+1}}\right|_{x=-1/2} \\&=& \frac{2}{3}\left(\frac{1}{6}\right)^n\end{eqnarray*}これらで再度極限をとって$$\sum_{m=0}^\infty\left(\sum_{n=0}^\infty a_{mn}\right)=\sum_{n=0}^\infty\left(\sum_{m=0}^\infty a_{mn}\right)=\frac{4}{5}$$正方形並べでは二項定理によって$$S_{mm}=\sum_{k=0}^m\left(-\frac{1}{2}\right)^k\sum_{l=0}^k\binom{k}{l}\left(-\frac{1}{2}\right)^l =\sum_{k=0}^m\left(-\frac{1}{4}\right)^k$$$$\therefore\quad\lim_{m\to\infty}S_{mm}=\frac{4}{5}$$
無限に続く $\{a_{mn}\}$ は $m,n$ の小さい方から次のように表される(この記法は前回参照)。\begin{equation}\begin{matrix}0 & -1 & 0 & 0 \\ 1 & 0 & -1 & 0\\ 0 & 1 & 0 &-1 \\ 0 & 0 & 1 & 0\end{matrix}\end{equation}(a) 二重級数は発散することを示せ。
(b) 逐次極限を求めよ。
(a) 正方形と、それより1列多くとった長方形を比較するとよい。$\epsilon=1$ ととると $\forall N$ に対して$$|S_{N,N+1}-S_{N,N}|=1 \ge\epsilon$$よってコーシー列ではないので発散する。
(b) $$\sum_{m=0}^\infty\left(\sum_{n=0}^\infty a_{mn}\right)=\sum_{m=0}^0 1 =1$$$$\sum_{n=0}^\infty\left(\sum_{m=0}^\infty a_{mn}\right)=-1$$
(a) $\displaystyle\sum_{m,n=1}^\infty\frac{1}{m^n}$ は収束するか。
(b) $\displaystyle\sum_{m=0,n=1}^\infty\frac{1}{(m+a)^n}$ , $(a>0)$ は収束するか。
(a)(b)ともに正項級数であるから、逐次極限を考えればよい。$$\sum_{n=1}^\infty\left(\sum_{m=1}^\infty\frac{1}{m^n}\right)=\lim_{n\to\infty}H_n +\zeta(2)+\zeta(3)+\cdots$$調和数 $H_n$ は発散するので、二重級数は発散する。
(b)はフルヴィッツゼータ関数の列となるが、同様に $n=1$ の部分で発散する。
次回はこちら:



Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。