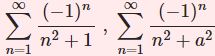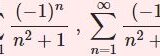\begin{equation}\sum_{n=1}^\infty\frac{1}{n^2+1}\tag{1}\end{equation}\begin{equation}\sum_{n=1}^\infty\frac{1}{n^2+a^2}\tag{2}\end{equation}
まずは1行目の値を求める方法を解説し,次にその例題として2行目を説明します.指数関数の複素フーリエ級数を求め,パーセヴァルの等式を利用することによってゴールにたどりつきます.
ここでこだわりたいのは,フーリエ級数の公式やパーセヴァルの等式に機械的に代入して進めるのではなく,もろもろの式がなぜ出てくるのかが分かるように説明していくということです.
類似した無限級数が過去記事にあります.
関数 $f(x)$ の $-\pi<x<\pi$ における複素フーリエ級数展開は$$f(x)=\sum^\infty_{n=-\infty}c_ne^{inx}$$ここでは正負別々に極限をとるのではなく,同じペースで極限をとります.つまり$$f(x)=\displaystyle\lim_{N\to\infty}\sum^N_{n=-N}c_ne^{inx}$$ということです.
さて今回は指数関数の級数展開$$e^x=\sum^\infty_{n=-\infty}c_ne^{inx}$$を考えます.$c_n$ を求めましょう.
まず両辺に $e^{-imx}$ をかけて積分します.$$\int_{-\pi}^\pi e^xe^{-imx}dx=\sum^\infty_{n=-\infty}c_n\int_{-\pi}^\pi e^{inx}e^{-imx}dx$$$$\therefore\;\frac{(-1)^m(e^\pi-e^{-\pi})}{1-im}=\sum^\infty_{n=-\infty}c_n\int_{-\pi}^\pi e^{i(n-m)x}dx$$右辺の積分は $n\neq m$ では $0$ となるので結局$$\frac{(-1)^m(e^\pi-e^{-\pi})}{1-im}=c_m\int_{-\pi}^\pi dx$$計算を進めると\begin{eqnarray*}c_m&=&\frac{(-1)^m(e^\pi-e^{-\pi})}{2\pi(1-im)}\\&=&\frac{\sinh\pi}{\pi}\frac{(-1)^m(1+im)}{m^2+1}\end{eqnarray*}以上より $e^x$ の複素フーリエ級数表示は$$e^x=\frac{\sinh\pi}{\pi}\sum^\infty_{n=-\infty}\frac{(-1)^n(1+in)}{n^2+1}e^{inx}\;\;(-\pi<x<\pi)$$となりました.
$$e^x=\sum^\infty_{n=-\infty}c_ne^{inx}$$の両辺を2乗します.$$e^{2x}=\sum^\infty_{m=-\infty}c_me^{imx}\sum^\infty_{n=-\infty}c_ne^{inx}$$これを $-\pi$ から $\pi$ まで積分すると右辺では $n+m=0$ 以外の項は $0$ になります.\begin{eqnarray*}\int_{-\pi}^\pi e^{2x}dx&=&\int_{-\pi}^\pi\sum^\infty_{m=-\infty}c_me^{imx}\sum^\infty_{n=-\infty}c_ne^{inx}dx\\&=&\sum^\infty_{m,n=-\infty}c_mc_n\int_{-\pi}^\pi e^{i(m+n)x}dx\\&=&\sum^\infty_{n=-\infty}c_nc_{-n}\int_{-\pi}^\pi dx\\&=&2\pi\sum^\infty_{n=-\infty}c_nc_{-n}\\&=&2\pi\frac{\sinh^2\pi}{\pi^2}\sum^\infty_{n=-\infty}\frac{(-1)^n(1+in)}{n^2+1}\frac{(-1)^n(1-in)}{n^2+1}\\&=&2\frac{\sinh^2\pi}{\pi}\sum^\infty_{n=-\infty}\frac{1}{n^2+1}\end{eqnarray*}これがパーセヴァルの等式に相当します.左辺の積分は\begin{equation}\int_{-\pi}^\pi e^{2x}dx=\sinh 2\pi=2\sinh\pi\cosh\pi\end{equation}なので\begin{eqnarray*}\sum^\infty_{n=-\infty}\frac{1}{n^2+1}&=&\frac{\pi}{2\sinh^2\pi}2\sinh\pi\cosh\pi\\&=&\frac{\pi\cosh\pi}{\sinh\pi}\\&=&\pi\coth\pi\end{eqnarray*}総和の範囲を正、負、0で分けて考えると\begin{equation}\sum^\infty_{n=-\infty}\frac{1}{n^2+1}=2\sum^\infty_{n=1}\frac{1}{n^2+1}+1\end{equation}となりますので
$$\sum^\infty_{n=1}\frac{1}{n^2+1}=\frac{1}{2}(\pi\coth\pi-1)$$
を得ます!
$e^{ax}$ の複素フーリエ展開を用いて,\begin{equation}\sum_{n=1}^\infty\frac{1}{n^2+a^2}\tag{2}\end{equation}を求めよ.
$$e^{ax}=\sum^\infty_{n=-\infty}c_ne^{inx}$$とおきます.両辺に $e^{-imx}$ をかけて積分すると$$\int_{-\pi}^\pi e^{(a-im)x}dx=\sum^\infty_{n=-\infty}c_n\int_{-\pi}^\pi e^{inx}e^{-imx}dx$$$$\therefore\;\frac{(-1)^m(e^{a\pi}-e^{-a\pi})}{a-im}=\sum^\infty_{n=-\infty}c_n\int_{-\pi}^\pi e^{i(n-m)x}dx$$右辺の積分は $n\neq m$ で $0$ となるので$$\frac{(-1)^m(e^{a\pi}-e^{-a\pi})}{a-im}=2\pi c_m$$計算を進めると\begin{eqnarray*}c_m&=&\frac{(-1)^m(e^{a\pi}-e^{-a\pi})}{2\pi(a-im)}\\&=&\frac{\sinh a\pi}{\pi}\frac{(-1)^m(a+im)}{m^2+a^2}\end{eqnarray*}以上より $e^{ax}$ の複素フーリエ級数表示は$$e^{ax}=\frac{\sinh a\pi}{\pi}\sum^\infty_{n=-\infty}\frac{(-1)^n(a+in)}{n^2+a^2}e^{inx}\;\;(-\pi<x<\pi)$$
続いて$$e^{ax}=\sum^\infty_{n=-\infty}c_ne^{inx}$$の両辺を2乗します.$$e^{2ax}=\sum^\infty_{m=-\infty}c_me^{imx}\sum^\infty_{n=-\infty}c_ne^{inx}$$これを $-\pi$ から $\pi$ まで積分すると右辺では $n+m=0$ 以外の項は $0$ になります.\begin{eqnarray*}\int_{-\pi}^\pi e^{2ax}dx&=&\int_{-\pi}^\pi\sum^\infty_{m=-\infty}c_me^{imx}\sum^\infty_{n=-\infty}c_ne^{inx}dx\\&=&\sum^\infty_{m,n=-\infty}c_mc_n\int_{-\pi}^\pi e^{i(m+n)x}dx\\&=&\sum^\infty_{n=-\infty}c_nc_{-n}\int_{-\pi}^\pi dx\\&=&2\pi\sum^\infty_{n=-\infty}c_nc_{-n}\\&=&2\pi\frac{\sinh^2\pi a}{\pi^2}\sum^\infty_{n=-\infty}\frac{(-1)^n(a+in)}{n^2+a^2}\frac{(-1)^n(a-in)}{n^2+a^2}\\&=&2\frac{\sinh^2\pi a}{\pi}\sum^\infty_{n=-\infty}\frac{1}{n^2+a^2}\end{eqnarray*}これがパーセヴァルの等式に相当します.左辺の積分は\begin{equation}\int_{-\pi}^\pi e^{2ax}dx=\frac{\sinh 2\pi a}{a}=\frac{2\sinh\pi a\cosh\pi a}{a}\end{equation}なので$$\sum^\infty_{n=-\infty}\frac{1}{n^2+a^2}=\frac{\pi}{a}\coth\pi a$$よって
$$\sum^\infty_{n=1}\frac{1}{n^2+a^2}=\frac{1}{2a}\left(\pi\coth\pi a-\frac{1}{a}\right)$$
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。