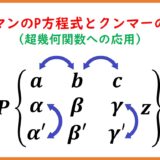
リーマンのP微分方程式を前提知識とします. 前々回はこちら:
前回はこちら:
参考文献はWhittaker & Watsonです。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
リーマンのP微分方程式\begin{eqnarray}&&u''+\left(\frac{1-\a-\a'}{z-a}+\frac{1-\b-\b'}{z-b}+\frac{1-\g-\g'}{z-c}\right)u'\\&&\quad+\left(\frac{\a\a'(a-b)(a-c)}{z-a}+\frac{\b\b'(b-a)(b-c)}{z-b}+\frac{\g\g'(c-a)(c-b)}{z-c}\right)\\&&\quad\quad\quad\times\frac{u}{(z-a)(z-b)(z-c)}=0\tag{0.1}\end{eqnarray}(ただし $\a+\a'+\b+\b'+\g+\g'=1$)
の解全体を次で表記する。\begin{equation}u(z)=P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}\tag{0.2}\end{equation}
任意のメビウス変換 $w=T(z)$ により、特異点が移ることを除いて不変。\begin{equation}P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}= P\left\{\begin{matrix}T(a) & T(b) & T(c)\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;w\right\}\tag{0.3}\end{equation}さらに次のような変換公式がある。\begin{equation}\left(\frac{z-a}{z-b}\right)^\mu\left(\frac{z-c}{z-b}\right)^\nu P\left\{\begin{matrix}a & b & c\\\a & \b & \g\\\a' & \b' & \g'\end{matrix}\;z\right\}= P\left\{\begin{matrix}a & b & c\\\a+\mu & \b-\mu-\nu & \g+\nu\\\a'+\mu & \b'-\mu-\nu & \g'+\nu\end{matrix}\;z\right\}\tag{0.4}\end{equation}(ただし、たとえば $b=\infty$ の場合は $(z-b)$ を $1$ に変更)。
これを応用して超幾何微分方程式へ帰着したり、超幾何関数の変換公式(Kummer's 24 solutions)を導出できました。それらの変換は線型変換(linear transformation)といいます。今回は2次変換(quadratic transformation)の基本を学びます。
二次変換公式については過去記事Aや過去記事Bでいくつか証明しました。微分方程式の解の形から導き出したり(今回もそれに近い)、級数や積分を変形するなどの方法がありました。しかしそのときは結果が先に分かっていて、後追いで示したにすぎません。どのようにして二次変換公式を発見するのでしょうか?
確定特異点が $\pm1,\infty$ で、解全体が次のように表記されるとします。\begin{equation}u(z)=P\left\{\begin{matrix}-1 & \infty & 1\\\g & 2\b & \g\\\g' & 2\b' & \g'\end{matrix}\;z\right\}\tag{1.1}\end{equation}ただし $\b+\b'+\g+\g'=1/2$ です。このような解構造を持つリーマンのP微分方程式は、(0.1)を変形して次のように表せます。\begin{equation}u''+\frac{2(1-\g-\g')z}{z^2-1}u'+\left(\frac{4\g\g'}{z^2-1}+4\b\b'\right)\frac{u}{z^2-1}=0\tag{1.2}\end{equation}ここで $w=z^2$ なる変数変換を行います。すると\begin{equation}\frac{d^2u}{dw^2}+\left(\frac{1}{2w}+\frac{1-\g-\g'}{w-1}\right)\frac{du}{dw}+\left(\frac{\g\g'}{w-1}+\b\b'\right)\frac{u}{w(w-1)}=0\tag{1.3}\end{equation}これもまたP方程式の形をしており、その解全体は\begin{equation}P\left\{\begin{matrix}0 & \infty & 1\\0 & \b & \g\\\frac{1}{2} & \b' & \g'\end{matrix}\;z^2\right\}\tag{1.4}\end{equation}したがって
\begin{equation}P\left\{\begin{matrix}0 & \infty & 1\\0 & \b & \g\\\frac{1}{2} & \b' & \g'\end{matrix}\;z^2\right\}=P\left\{\begin{matrix}-1 & \infty & 1\\\g & 2\b & \g\\\g' & 2\b' & \g'\end{matrix}\;z\right\}\tag{1.5}\end{equation}ただし $\b+\b'+\g+\g'=1/2$.
(1.5)の左辺に(0.4)を用いて$$P\left\{\begin{matrix}0 & \infty & 1\\0 & \b & \g\\\frac{1}{2} & \b' & \g'\end{matrix}\;z^2\right\}=(z^2-1)^\g P\left\{\begin{matrix}0 & \infty & 1\\0 & \b+\g & 0\\\frac{1}{2} & \b'+\g & \g'-\g\end{matrix}\;z^2\right\}$$(1.5)の右辺に(0.4)および(0.3)を適用します。メビウス変換は $T(z)=\frac{z+1}{2}$ です。\begin{eqnarray*}P\left\{\begin{matrix}-1 & \infty & 1\\\g & 2\b & \g\\\g' & 2\b' & \g'\end{matrix}\;z\right\}&=& (z^2-1)^\g P\left\{\begin{matrix}-1 & \infty & 1\\0 & 2\b+2\g & 0\\\g'-\g & 2\b'+2\g & \g'-\g\end{matrix}\;z\right\} \\&=& (z^2-1)^\g P\left\{\begin{matrix}0 & \infty & 1\\0 & 2\b+2\g & 0\\\g'-\g & 2\b'+2\g & \g'-\g\end{matrix}\;\frac{z+1}{2}\right\}\end{eqnarray*}よって\begin{equation}P\left\{\begin{matrix}0 & \infty & 1\\0 & \b+\g & 0\\\frac{1}{2} & \b'+\g & \g'-\g\end{matrix}\;z^2\right\}=P\left\{\begin{matrix}0 & \infty & 1\\0 & 2\b+2\g & 0\\\g'-\g & 2\b'+2\g & \g'-\g\end{matrix}\;\frac{z+1}{2}\right\}\tag{1.6}\end{equation}この両辺は超幾何微分方程式の解の形になっています。任意定数 $\b,\b'$,$\g,\g'$ に対して $\b+\b'+\g+\g'=1/2$ なる条件が課されていますので、3個の定数 $a,b,c$ に置きなおしましょう。$\b+\g=a$ , $\b+\b'=b$ , $\g'=c$ とおくと $\g=a+b+c-\frac{1}{2}$ となります。よって、超幾何微分方程式に関する次の定理が示されます。
\begin{equation}P\left\{\begin{matrix}0 & \infty & 1\\0 & a & 0\\\frac{1}{2} & b & \frac{1}{2}-a-b\end{matrix}\;z^2\right\}=P\left\{\begin{matrix}0 & \infty & 1\\0 & 2a & 0\\\frac{1}{2}-a-b & 2b & \frac{1}{2}-a-b\end{matrix}\;\frac{z+1}{2}\right\}\tag{1.7}\end{equation}
定理1Bの左辺を方程式にすると$$u''+\left(\frac{1/2}{z^2}+\frac{a+b+1/2}{z^2-1}\right)u'+\frac{abu}{z^2(z^2-1)}=0$$変形すると\begin{equation}w(1-w)u''+\left\{\frac{1}{2}-(a+b+1)w\right\}u'-abu=0\;(w=z^2)\tag{2.1}\end{equation}同様に定理1Bの右辺を方程式にすると\begin{equation}w(1-w)u''+\left\{a+b+\frac{1}{2}-(2a+2b+1)w\right\}u'-4abu=0\;(w=\frac{1+z}{2})\tag{2.2}\end{equation}です。定理1Bは(2.1)と(2.2)が方程式として同じである、すなわち解が全体として一致するといっています。なので(2.1)の任意の特殊解は、(2.2)の特殊解2つの線型結合で表されます。これが超幾何関数の二次変換の基本です。
超幾何微分方程式は一般に\begin{equation}z(1-z)u''+[C-(A+B+1)z]u'-ABz=0\tag{2.3}\end{equation}の形になっており、その代表的な特殊解は\begin{equation}u=F\left[\begin{matrix}A,B\\C\end{matrix};z\right]\tag{2.4}\end{equation}なのでした。前回の記事でKummer's 24 solutionsつまり(2.4)を含めて24つの特殊解を挙げています。これらを組み合わせて二次変換公式を作ればいいのです。
以下、解の名称 $u_1,u_2,\cdots,u_6$ は前回の記事のKummer's 24 solutions一覧のものを示します。
(2.1)の解から $u_1$ を選びます。$$F\left[\begin{matrix}a,b\\\frac{1}{2}\end{matrix};z^2\right]$$(2.2)の解から次の $u_1$ と $u_2$ を選びます。$z=0$ で正則で分岐点を持たないからです。$$F\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1+z}{2}\right]\;,\;F\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1-z}{2}\right]$$3つは従属関係にありますので\begin{equation}F\left[\begin{matrix}a,b\\\frac{1}{2}\end{matrix};z^2\right]=AF\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1+z}{2}\right]+BF\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1-z}{2}\right]\tag{3.1}\end{equation}$z=0$ で$$1=(A+B)F\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1}{2}\right]$$$z=1$ で$$F\left[\begin{matrix}a,b\\\frac{1}{2}\end{matrix};1\right]=AF\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};1\right]+B$$$A,B$ の連立方程式ができましたが、前者は過去記事で証明した\begin{equation}F\left(\begin{matrix}a,b\\\frac{a+b+1}{2}\end{matrix};z\right) = F\left(\begin{matrix}\frac{a}{2},\frac{b}{2}\\\frac{a+b+1}{2}\end{matrix};4z(1-z)\right)\tag{3.2}\end{equation}で $z=1/2$ とするとよいです。ガンマ関数に直し、相反公式などで計算すると$$A=B=\frac{\G(a+\frac{1}{2})\G(b+\frac{1}{2})}{2\sqrt{\pi}\G(a+b+\frac{1}{2})}$$これで(3.1)の二次変換公式が完成しました。
(2.1)の解から $u_2$ を、(2.2)の解から $u_1$ , $u_2$ を選んで線型結合すると\begin{equation}F\left[\begin{matrix}a,b\\a+b+\frac{1}{2}\end{matrix};1-z^2\right]=AF\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1+z}{2}\right]+BF\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1-z}{2}\right]\tag{4.1}\end{equation}$1-z^2$ を $z$ に変換すると\begin{equation}F\left[\begin{matrix}a,b\\a+b+\frac{1}{2}\end{matrix};z\right]=AF\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1+\sqrt{1-z}}{2}\right]+BF\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1-\sqrt{1-z}}{2}\right]\tag{4.2}\end{equation}根号は、中身が非負の実数なら、非負の実数になるようにとります。
二次変換を作るときには、Higher transcendental function vol1に倣って $z=0$ の近傍で成立するようにしておきます。(4.1)のままでは左辺がそうなっていません。
$z=0,1$ を代入して $A=0$ , $B=1$ を得ます。\begin{equation}F\left[\begin{matrix}a,b\\a+b+\frac{1}{2}\end{matrix};z\right]=F\left[\begin{matrix}2a,2b\\a+b+\frac{1}{2}\end{matrix};\frac{1-\sqrt{1-z}}{2}\right]\tag{4.3}\end{equation}
(2.1)の解から $u_3$ を、(2.2)の解から $u_3$ , $u_4$ を選んで線型結合すると$$z^{-2a}F\left[\begin{matrix}a,a+\frac{1}{2}\\a-b+1\end{matrix};\frac{1}{z^2}\right]=A(z+1)^{-2a}F\left[\begin{matrix}2a,a-b+\frac{1}{2}\\2a-2b+1\end{matrix};\frac{2}{1+z}\right]+B(z+1)^{-2b}F\left[\begin{matrix}2b,b-a+\frac{1}{2}\\2b-2a+1\end{matrix};\frac{2}{1+z}\right]$$$1/z^2$ を $z^2$ に変換しておきます。また $a-b+1=c$ とパラメータを置き換えて$$F\left[\begin{matrix}a,a+\frac{1}{2}\\c\end{matrix};z^2\right]=A(1+z)^{-2a}F\left[\begin{matrix}2a,c-\frac{1}{2}\\2c-1\end{matrix};\frac{2z}{1+z}\right]+\frac{Bz^{2-2c}}{(1+z)^{2a-2c+2}}F\left[\begin{matrix}2b,b-a+\frac{1}{2}\\2b-2a+1\end{matrix};\frac{2z}{1+z}\right]$$右辺第2項は $z=0$ で特異点になりますので $B=0$ です。$z=0$ を代入すると $A=1$ となります。よって\begin{equation}F\left[\begin{matrix}a,a+\frac{1}{2}\\c\end{matrix};z^2\right]=(1+z)^{-2a}F\left[\begin{matrix}2a,c-\frac{1}{2}\\2c-1\end{matrix};\frac{2z}{1+z}\right]\tag{5.1}\end{equation}
$\g+\g'=1/3$ として$$P\left\{\begin{matrix}0 & \infty & 1\\0 & 0 & \g\\\frac{1}{3} & \frac{1}{3} & \g'\end{matrix}\;z^3\right\}=P\left\{\begin{matrix}1 & \omega & \omega^2\\\g & \g & \g\\\g' & \g' & \g'\end{matrix}\;z\right\}$$なる公式があります。右辺が満たす方程式を書いて$$\frac{1}{z-1}+\frac{1}{z-\omega}+\frac{1}{z-\omega^2}=\frac{3z^2}{z^3-1}$$$$\frac{1}{z-1}+\frac{\omega^2}{z-\omega}+\frac{\omega}{z-\omega^2}=\frac{3z}{z^3-1}$$を使うと$$u''+\frac{2z^2}{z^3-1}u'+\frac{9\g\g' z}{(z^3-1)^2}u=0$$となりますので、$\zeta=z^3$ と置換して得られます。
この公式を超幾何微分方程式になるように変換すると$$P\left\{\begin{matrix}0 & \infty & 1\\0 & \g & 0\\\frac{1}{3} & \g+\frac{1}{3} & \frac{1}{3}-2\g\end{matrix}\;z^3\right\}=(z-\omega^2)^{-3\g} P\left\{\begin{matrix}0 & \infty & 1\\0 & 3\g & 0\\\frac{1}{3}-2\g & \g+\frac{1}{3} & \frac{1}{3}-2\g\end{matrix}\;\frac{(1+\omega)(z-\omega)}{(z-\omega^2)}\right\}$$この先は難儀そうです。左辺から $u_1$ を、右辺から $u_1$ , $u_2$ を選んでできたと思われる式が、Higher transcendental function vol1の2.11(37)に見られますが、あまりすっきりしていません。。Goursatが導いたようなきれいな3次変換はどのように得られるのでしょう?2次変換との合わせ技なども考えなくてはいけないかも。
メモ:E.G.C.Poole,"Introduction to the theory of linear differential equations"のVI.§25とかVII.§31あたりが参考になるか??あるいはGoursat,"Sur l'équation différentielle linéaire qui admet pour intégrale la série hypergéométrique."の65ページから頑張るか。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。