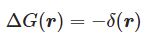高等学校では点電荷がつくる電位の公式を習います。今回は電磁気学の基礎を論じる上ですべての出発点となる真空中のマクスウェル方程式からこの公式を導き出します。点電荷を扱う際にデルタ関数という変わった関数が出てきますが、その扱い方を知ることも大切です。
高等学校の物理の知識によると点電荷 $q$ が距離 $r$の位置につくる電位 $\phi$ は$$\phi=\frac{q}{4\pi\epsilon r}$$と表されます。今回はこの式をマクスウェル方程式から導出したいと思います。
真空中のマクスウェル方程式から $$\phi(r)=\frac{q}{4\pi\epsilon r}$$ を導け．
マクスウェル方程式が４つの方程式の組からなることはよく知られていますが、今回は磁場はありませんので必要なのは１つだけです。
\begin{equation}\nabla\cdot\boldsymbol{E}=\frac{\rho}{\epsilon}\tag{1}\end{equation}
あと必要なのは、静電場と電位（静電ポテンシャル）の関係\begin{equation}\boldsymbol{E}=-\nabla\phi\end{equation}です。これを式(1)に代入すると\begin{equation}\Delta\phi=-\frac{\rho}{\epsilon}\end{equation}を得ます。これが解くべき式であり、電荷密度 $\rho(\boldsymbol{x})$ が与えられたときに $\phi (\boldsymbol{x}) $ がどう決まるかを記述した微分方程式です。これから解いていきますが、話をシンプルにするためにグリーン関数についての話題は避けます。
「密度」というと連続的に電荷が分布していることを想定しますが、点電荷の場合はどう表せばいいでしょうか。そこで現れるのがデルタ関数です。デルタ関数 $\delta(x)$ は $x=0$ のとき無限大となり、他で $0$ となる変な関数です。さらに $\delta(x)$ を $(-\infty,\infty)$ で積分すると $1$ となります。
今、原点に点電荷 $q$ があるとします。このとき、$\boldsymbol{r}=(x,y,z)$ とすると電荷密度は
\begin{equation}\rho(\boldsymbol{r})=q\delta(x)\delta(y)\delta(z)\tag{2}\end{equation}と表されます。この式を見ると原点以外では3つのデルタ関数のうち少なくとも1つは $0$ なので $\rho=0$ となります。また原点では $\rho$ は無限大となりますが、電荷が1点に集まっていることから密度が有限でないことは理にかなっています。電荷密度を空間全体で積分すると、デルタ関数の性質から
$$\iiint\rho dV=q\int_{-\infty}^{\infty}\delta(x)dx\int_{-\infty}^{\infty}\delta(y)dy\int_{-\infty}^{\infty}\delta(z)dz=q$$
これは空間に分布する電荷の合計が $q$ であることを示しており、問題の状況と合致しています。よって電荷密度は(2)で与えればよいことになります。
よって解くべき方程式は\begin{equation}\Delta\phi(\boldsymbol{r})=-\frac{q}{\epsilon}\delta^3(\boldsymbol{r})\tag{3}\end{equation}となります。ただし $\delta^3(\boldsymbol{r})\equiv\delta(x)\delta(y)\delta(z)$ としています。
さて $|\boldsymbol{r}|=r$ と書くことにします。$1/r$ の勾配を考えると
\begin{eqnarray}\nabla\frac{1}{r}&=&\left(\frac{\partial}{\partial x}\frac{1}{r},\frac{\partial}{\partial y}\frac{1}{r},\frac{\partial}{\partial z}\frac{1}{r}\right)\\&=&\left(-\frac{x}{r^3},-\frac{y}{r^3},-\frac{z}{r^3}\right)\\&=&-\frac{\boldsymbol{r}}{r^3}\end{eqnarray}どうして急にそんな話をするんだという感じですが、まぁ事情を知っているからこそです（※一番下に参考リンクつけときます）。
さらにこの発散をとります。
\begin{eqnarray}\Delta\frac{1}{r}&=&\nabla\cdot\nabla\frac{1}{r}\\&=&\nabla\cdot\left(-\frac{\boldsymbol{r}}{r^3}\right)\\&=&-\frac{1}{r^3}+\frac{3x^2}{r^5}-\frac{1}{r^3}+\frac{3y^2}{r^5}-\frac{1}{r^3}+\frac{3z^2}{r^5}\\&=& 0\end{eqnarray}
というわけで $r\neq0$ においては\begin{equation}\Delta\frac{1}{r}=0\end{equation}じゃあ $r=0$ ではどうなのでしょう。$r$ の逆数が式にありますから無限大じゃないかと想像できます。$r=0$ で無限大でそれ以外ではゼロってまさにデルタ関数じゃないか？と思うわけです。そこで $\Delta\frac{1}{r}$ を全空間にわたって積分してみましょう。\begin{eqnarray}\iiint\Delta\frac{1}{r}dV&=&\iiint\nabla\cdot\left(\nabla\frac{1}{r}\right)dV\\&=&-\iiint\nabla\cdot\left(\frac{\boldsymbol{r}}{r^3}\right)dV\end{eqnarray}ここで積分する範囲を半径 $R$ の球とするとあとで $R\to\infty$ とすれば全空間になります。ガウスの法則から\begin{equation}-\iiint\nabla\cdot\left(\frac{\boldsymbol{r}}{r^3}\right)dV=-\iint_S\left(\frac{\boldsymbol{r}}{R^3}\right)\cdot\boldsymbol{n}dS\end{equation}ここで $S$ は球面、$dS$ は球面上の微小面積、$\boldsymbol{n}$ は球面の単位法線ベクトルです。球面の法線は動径方向ですから $\boldsymbol{n}=\boldsymbol{e}_r$ であり、$\boldsymbol{r}\cdot\boldsymbol{e}_r=r=R$ となりますので\begin{equation}-\iint_S\left(\frac{\boldsymbol{r}}{R^3}\right)\cdot\boldsymbol{n}dS=-\iint_S\frac{1}{R^2}dS\end{equation}球面における座標系に変換します。
\begin{eqnarray}x&=&R\sin\theta\cos\phi\\y&=&R\sin\theta\sin\phi\\z&=&R\cos\theta\end{eqnarray}微小面積は
$$dS=R^2\sin\theta d\theta d\phi$$ですので\begin{eqnarray}-\iint_S\frac{1}{R^2}dS&=&-\int_0^{2\pi}d\phi\int^\pi_0 d\theta\frac{1}{R^2}R^2\sin\theta\\&=&-\int_0^{2\pi}d\phi\int^\pi_0\sin\theta d\theta\\&=&-4\pi\end{eqnarray}以上から$$\iiint\Delta\frac{1}{r}dV=-4\pi$$
ここまでをまとめると $\Delta\frac{1}{r}$ は原点以外でゼロ、原点で無限大、全空間で積分すると $-4\pi$ という性質をもっています。つまり\begin{equation}\Delta\frac{1}{r}=-4\pi\delta^3(\boldsymbol{r})\end{equation}となるわけです。両辺に $\frac{q}{4\pi\epsilon}$ をかけると$$\Delta\frac{q}{4\pi\epsilon r}=-\frac{q}{\epsilon}\delta^3(\boldsymbol{r})$$解きたい微分方程式(3)と見比べると\begin{equation}\phi(\boldsymbol{r})=\frac{q}{4\pi\epsilon r}\end{equation}と分かります。不定性はありますが、無限遠で $\phi=0$ の条件を課すことでこの解を得ることができます。
以上から、マクスウェル方程式からスタートして点電荷がつくる電位の式を求めることができました！
※のリンク
【物理数学】N次元グリーン関数の解法(1) Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
