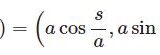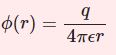高等学校では磁場を横切る導体棒に生じる誘導起電力 $V=vBl$ を学習します。しかし電磁誘導によって電流が流れると導体棒が磁場から力を受けるため、ほうっておくと減速してしまうのです。ではどのように減速していくか、導体棒の運動方程式を立てて解いてみたいと思います。一階の方程式なので微分方程式の基本練習になるかと思います。
下図はおなじみの回路である。導体棒の質量を $m$ とする。初速度 $v(0)=v_0$ (右向き)とすると、時刻 $t$ における導体棒の速度 $v(t)$ などを示しながら、この導体棒が今後どうなっていくか考察せよ。
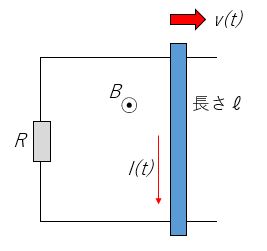
物体の運動について論ずるなら運動方程式を立てるのが一番です。図のように導体棒が右へ動くと、回路内を画面手前向きに貫く磁束 $\Phi$ が増加し、導体棒内に下向きの誘導起電力 $V(t)=v(t)Bl$ が発生します。すると回路を流れる電流はオームの法則により$$I(t)=\frac{Bl}{R}v(t)$$と書くことができます。
さてこの電流は磁場と垂直な向きに流れていますので、磁場から左向きの力を受けます(棒が横に動いているので電流の向きは、厳密にはそれとの合成ベクトルの向きとなるのでしょうが、無視します)。だからどんどん減速してしまうのですね。もし減速しないのだとしたら、何もしなくても慣性で延々と右へ移動してその間ずっと電流が走り続けます。ならば世間の電力問題は解決しそうですが、そうはいかないということです。
右向きを正方向とするとその力は$$F(t)=-I(t)Bl$$と表せます。先ほどの電流の式および $F=ma$ から$$m\frac{dv}{dt}=-\frac{B^2l^2}{R}v(t)$$変形して$$\frac{dv}{dt}=-\frac{B^2l^2}{mR}v(t)$$
これが導体棒の運動方程式となります。速度 $v$ に関する一階微分方程式ですね。
では微分方程式を解きます。これは変数分離が可能で$$\frac{dv}{v}= -\frac{B^2l^2}{mR}dt$$これを $t=0$ から時刻 $t$ まで積分すると$$\int^{v(t)}_{v(0)} \frac{dv}{v} = -\frac{B^2l^2}{mR} \int^t_0dt$$$$\therefore\;\log\frac{v(t)}{v_0}= -\frac{B^2l^2}{mR}t$$ $v(t)$ について解くと
$$v(t)=v_0e^{-\frac{B^2l^2}{mR}t}$$
なのでその速度は指数関数的に落ちていき、$t\to\infty$ の極限では静止します。
ではこの棒はどこまで行くのでしょうか。時刻 $0$ から無限大までの間に進む変位を求めてみましょう。変位は速度の積分ですから\begin{eqnarray*}x_\infty&=&\int_0^\infty v(t)dt\\&=&v_0 \int_0^\infty e^{-\frac{B^2l^2}{mR}t}dt\\&=&-v_0\frac{mR}{B^2l^2}\Bigl[ e^{-\frac{B^2l^2}{mR}t} \Bigr]^\infty_0\\&=& \frac{mRv_0}{B^2l^2}\end{eqnarray*} よってこの棒は果てなくどこまでも進むのではなく、有限の距離しか運動しないことが分かります。
また速度が落ちていくならば誘導起電力も下がり、流れる電流も減少します。時刻 $t$ における電流値は$$I(t)= \frac{v_0Bl}{R}e^{-\frac{B^2l^2}{mR}t}$$
以上で今回のテーマは終わりなのですが、右向きに一定の外力を加えたときに導体棒がどう動くか検証します。微分方程式の練習になります。
冒頭の回路において初速 $0$ とし、右向きに一定の外力 $f$ を加え続けるときの導体棒の運動を考察せよ。
右向きを正方向とします。時刻 $t$ において棒にかかる力は、ローレンツ力 $-I(t)Bl$ および $f$ です。 よって運動方程式は$$m\frac{dv}{dt}=f-\frac{B^2l^2}{R}v(t)$$変数分離へ持ち込みます。$$\frac{dv}{\frac{Rf}{B^2l^2}-v}=\frac{B^2l^2}{mR}dt$$初速 $v(0)=0$ ですので積分をとると$$\int^{v(t)}_0\frac{dv}{\frac{Rf}{B^2l^2}-v}=\int^t_0\frac{B^2l^2}{mR}dt$$ $$\therefore\;v(t)=\frac{Rf}{B^2l^2}\left(1-e^{-\frac{B^2l^2}{mR}t}\right)$$
つまり導体棒は加速し続けるもだんだん速度の伸びが悪くなり、十分に時間がたつと終端速度 $\displaystyle\frac{Rf}{B^2l^2}$ の等速運動となります。ここからはずっと状態が変わらないので「定常状態」とでも名付けましょう。
また電流の時間変化は$$I(t)=\frac{f}{Bl}\left(1-e^{-\frac{B^2l^2}{mR}t}\right)$$なので十分時間がたった時の電流値は$I_{\infty}=\displaystyle\frac{f}{Bl} $ となります。つまり定常状態になってからの抵抗における消費電力は$$P=RI_{\infty}^2=\frac{Rf^2}{B^2l^2}$$ 外力の仕事率は$$fv_\infty=\frac{Rf^2}{B^2l^2} $$となります。外力の仕事と消費電力は一致しており、外力を加え続けないと同じ電流は流せないことが分かります。電流を流し続けるのって大変なんだなぁと(?)
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。