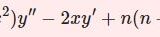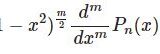じゃあ今度は落体運動を微分方程式で考察していくよ!

落体の運動は高校のとき運動方程式よりも先に勉強したな。速度や加速度を理解しているかのバロメータのような単元でもあった。そこではこんな感じの種類があったと思う。
- 自由落下$$y=\frac{1}{2}gt^2$$
- 鉛直投げ下ろし$$y=v_0t+\frac{1}{2}gt^2$$
- 鉛直投げ上げ$$y=v_0t-\frac{1}{2}gt^2$$
- 水平投射$$x=v_0t\;,\;y=\frac{1}{2}gt^2$$
- 斜方投射$$x=v_0\cos\theta\cdot t\;,\;y=v_0\sin\theta\cdot t-\frac{1}{2}gt^2$$

共通するのはこれらはすべて重力 $mg$ による運動だってこと。

そうなんだ。これらは全部、力 $mg$ のもとで運動方程式 $F=ma$ を解いただけなんだ。でも座標の取り方と初期条件からこんなにも違いが出てくるんだ。

まずは自由落下いくよ!解き方をよく見ておいて。これが理解できればこの後のも全部分かるさ。
下方向が正、時刻0での位置を原点とする。
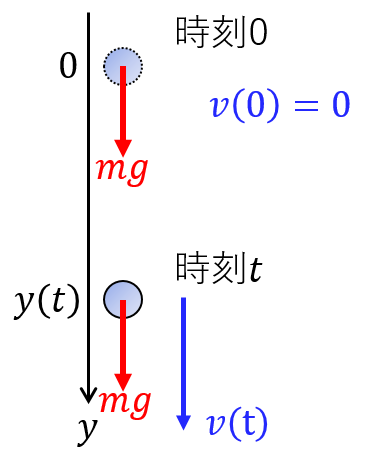
重力は下向きなので正であり $F=mg$ と書ける。よって運動方程式より $a(t)=g$ なる式が立つ。すなわち求める微分方程式は$$\frac{d^2y}{dt^2}=g$$時間で積分して$$v(t)=\frac{dy}{dt}=gt+c_1$$初期条件 $v(0)=0$ を代入すると $c_1=0$ になるので$$\frac{dy}{dt}=gt$$もう1度積分して$$y(t)=\frac{1}{2}gt^2+c_2$$初期条件 $y(0)=0$ を代入すると $c_2=0$ だから求める解は$$y(t)=\frac{1}{2}gt^2$$

使用した物理法則はニュートンの運動方程式ただ1つだったね。あとはすべて積分をはじめとした数学的操作を機械的にやっただけというのがポイントさ。

この調子でほかのもいけそうだな。
下方向が正、時刻0での位置を原点にとる。初速度は $v_0$ である。
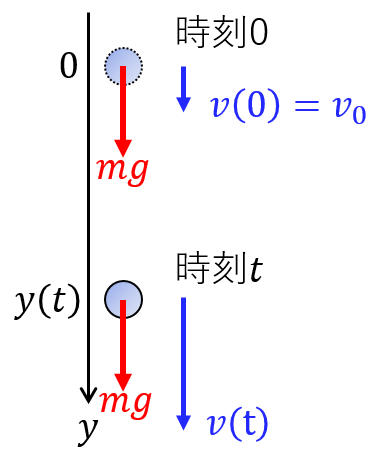
重力は下向きなので正であり $F=mg$ である。よって運動方程式より $a(t)=g$ なる式が立つ。すなわち求める微分方程式は$$\frac{d^2y}{dt^2}=g$$時間で積分して$$v(t)=\frac{dy}{dt}=gt+c_1$$初期条件 $v(0)=v_0$ を代入すると $c_1=v_0$ になるので$$v(t)=\frac{dy}{dt}=v_0+gt$$もう1度積分して$$y(t)=v_0t+\frac{1}{2}gt^2+c_2$$初期条件 $y(0)=0$ を代入すると $c_2=0$ だから求める解は$$y(t)=v_0t+\frac{1}{2}gt^2$$

やっぱり物理法則は運動方程式だた1つで、あとは数学だったね。ちなみに積分定数が出ないようにするには、範囲を適切に指定して定積分するという方法があるよ。下の例を見てみて!
$\frac{dy}{dt}=v_0+gt$ は変形すると$$dy=(v_0+gt)dt$$この両辺を定積分する。$y$ と $t$ の範囲を正しく対応させよう。
| 時刻 $t$ | $0$ | → | $t$ |
| 位置 $y$ | $0$ | → | $y(t)$ |
よって定積分は$$\int_0^{y(t)}dy=\int_0^t(v_0+gt)dt$$$$\therefore\quad y(t)= v_0t+\frac{1}{2}gt^2 $$

自由落下と同じ座標設定だったけど初期条件 $v_0$ があるだけで式が結構変わったな。

多様な式が1つの法則から生まれる。感動的なんだ!
この次の鉛直投げ上げは、座標設定の図だけ見て挑戦してみてほしい。
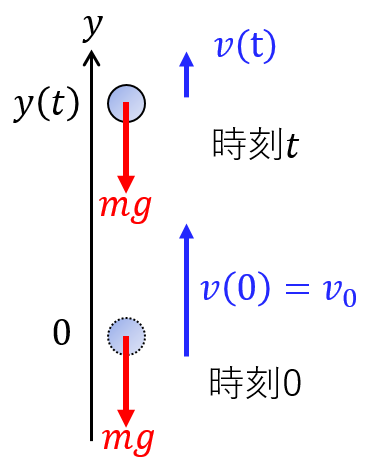
重力は下向きなので負であり $F=-mg$ である。よって運動方程式より $a(t)=-g$ なる式が立つ。すなわち求める微分方程式は$$\frac{d^2y}{dt^2}=-g$$時間で積分して$$v(t)=\frac{dy}{dt}=-gt+c_1$$初期条件 $v(0)=v_0$ を代入すると $c_1=v_0$ になるので$$v(t)=\frac{dy}{dt}=v_0-gt$$もう1度積分して$$y(t)=v_0t-\frac{1}{2}gt^2+c_2$$初期条件 $y(0)=0$ を代入すると $c_2=0$ だから求める解は$$y(t)=v_0t-\frac{1}{2}gt^2$$
$v(t)$ , $y(t)$ のグラフは次のようになる。
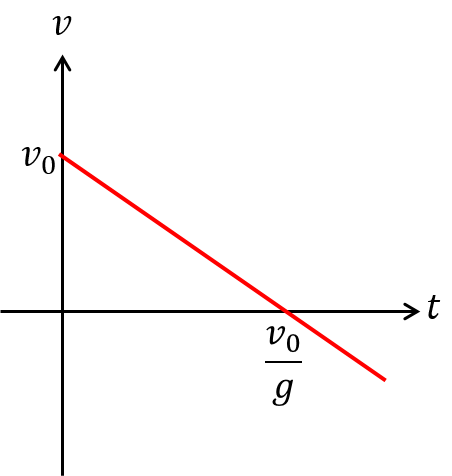
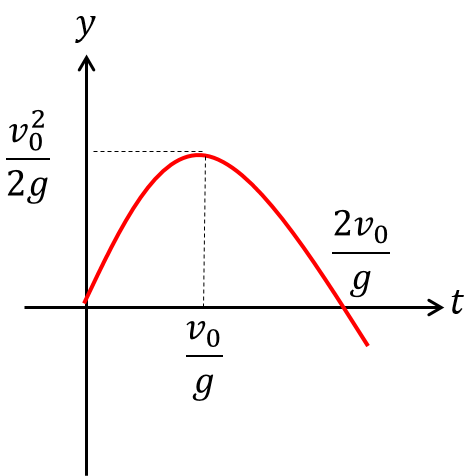

やること同じで飽き飽きだ!

同じということが身に染みて分かれば目標達成さ。次が最後だよ。
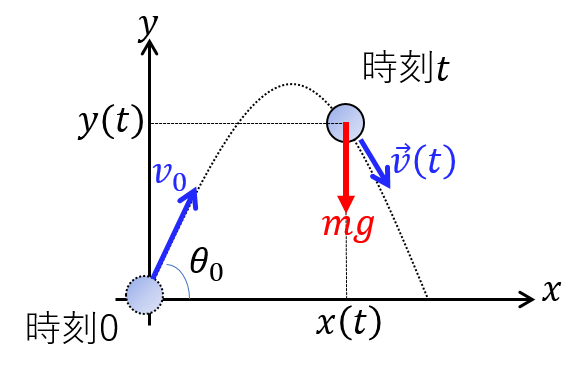
ベクトルを太字で表す。重力は下向きのベクトルであり $\boldsymbol{F}=(0,-mg)$ と書ける。運動方程式は $ \boldsymbol{F}=m\boldsymbol{a}(t)$ だから $x,y$ それぞれの成分で表示すると$$\begin{cases}a_x(t)&=&0\\a_y(t)&=&-g\end{cases}$$よって求める微分方程式は$$\begin{cases}\displaystyle\frac{d^2x}{dt^2}&=&0\\ \displaystyle\frac{d^2y}{dt^2} &=&-g\end{cases}$$これらの解き方はさんざんやってきたとおりだが、初期条件をしっかり確認しておく。$$\begin{cases}x(0)&=&0\\y(0)&=&0\\v_x(0)&=&v_0\cos\theta_0\\v_y(0)&=&v_0\sin\theta_0\end{cases}$$
あとは積分を繰り返すだけ。$$x(t)=v_0t\cos\theta_0$$$$y(t)=v_0t\sin\theta_0-\frac{1}{2}gt^2$$

説明が雑になってきたけど大丈夫だと思う。
微積分もベクトルも単に数学的操作だ。斜方投射もやっぱりこれまでと同じだったな。
物体の運動のようすはぱっと見で全く違うのに、面白いな。

水平投射は飛ばしたよ。よかったらやってみてね!

ぼくから応用問題を出すよ。
物体をそっと離して落下させるとき、空気抵抗があるといつか終端速度に達して、そのあとは等速直線運動で落下していくってのがあったよね。
ちょっと難しいけどやってみよう。数学IIIをやったなら大丈夫さ!
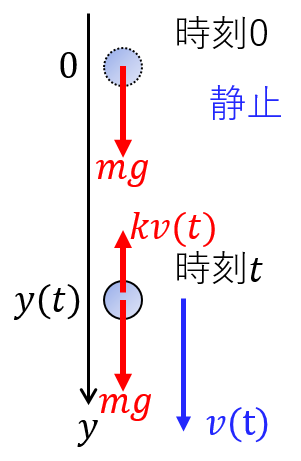
空気抵抗はいろいろなモデルがあるが、ここでは 落下速度に比例した力 $kv$ を逆向きに受けると仮定しよう。はじめの速度は$0$だから空気抵抗は0からスタートしてだんだん大きくなるので $mg>kv$ である。このとき運動方程式は $ma=mg-kv$ すなわち $$\frac{dv}{dt}=g-\frac{k}{m}v$$変形すると$$dt=\frac{dv}{g-\frac{k}{m}v}$$積分して初期条件 $v(0)=0$ を取り入れれば$$t=-\frac{m}{k}\log(1-\frac{kv}{mg})$$$$\therefore \quad v(t)=\frac{mg}{k}(1-e^{-\frac{k}{m}t})$$時刻 $t$ を大きくしていけば速度 $v$ は$mg/k$ へ収束していく(終端速度)。
さらに積分して初期条件 $y(0)=0$ を取り入れれば$$y(t)=\frac{mg}{k}\left[t-\frac{m}{k}(1-e^{-\frac{k}{m}t})\right]$$となり、時刻 $t$ における座標が求まった。
微積分と高校物理シリーズ
【H7】単振り子の方程式と厳密解
【H6】ベクトルの極座標成分
【H5】等速・非等速円運動と微分方程式

【H4】ばねの微分方程式 水平・鉛直・空気抵抗
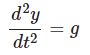
【H3】落体運動の法則はただ1つ
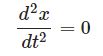
【H2】力がゼロの運動方程式と等速直線運動
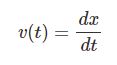
【H1】力学の表現と本シリーズの意義
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。