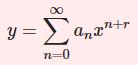「微積分と高校物理（仮）」というシリーズをスタートさせようと思います。高校物理をなるべく少ない原理で説明していきたい。それには微分方程式を駆使することが大切です。まずは力学から見てみましょう。
力学という分野は、物体がどのように動いていくかを記述する学問なんだ。
いつ、どこに物体があるのかが数値で表される必要があるんだね。
うん。だから座標を設定するのが出発点さ。物体の位置は時間によって変わるから、時間の関数になるんだ。どこを原点にするか、どっち方向を $x$ 軸とするかによって値が変わってくるから、あらかじめ座標を決めておくのが大事。
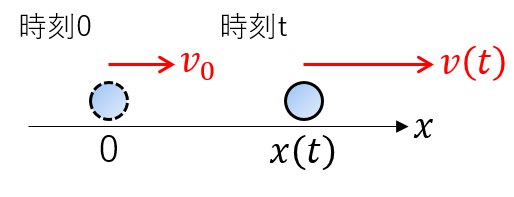
時刻0を原点にしてみた。任意の時刻 $t$ における座標は $x(t)$ と書くと便利だな。速度も同様に $v(t)$ と書こう。この場合初速度は $v(0)=v_0$ だ。
高校物理では微積が使えないからダメだったけど実際$$v(t)=\frac{dx}{dt}$$の関係があるんだ。位置の変化 $\Delta x$ を「変位」というよ。$\Delta x$ だけ位置が変わるのにかかった時間を $\Delta t$ とおけば平均の速度は$$\frac{\Delta x}{\Delta t}=\bar{v}$$これを $\Delta t\to 0$ とした極限が瞬間の速度すなわち $v(t)$ なのさ。
速度の変化を $\Delta v$ としたら平均の加速度は$$\frac{\Delta v}{\Delta t}$$と表されるのも習った！
変位と速度の関係と同じだね。つまり時刻 $t$ における加速度は$$a(t)=\frac{dv}{dt}=\frac{d^2x}{dt^2}$$と書けるわけなんだ。
平面・立体の場合も $x,y,z$ それぞれに対して同じ式が成り立つはずだな。
うむ！$$v_y(t)=\frac{dy}{dt}$$とか$$a_z(t)=\frac{d^2z}{dt^2}$$とかみたいに書くんだよ。
位置、速度、加速度は全部ベクトルだよ。2次元なら位置ベクトル $(x,y)$、速度ベクトル $(v_x,v_y)$、加速度ベクトルは $(a_x,a_y)$ なんだ。そしてそれぞれのベクトルには大きさ（絶対値）が定義されるよ。位置ベクトルの大きさは原点からの距離、速度ベクトルの大きさは速さ、加速度ベクトルの大きさは加速度の大きさなのさ。
微分なら機械的に計算できるからいいよね。高校のときは微積分が使えなかったから単元ごとにあの手この手で $v$ や $a$ の公式を導いていた気がする。
それはそれで大事なことなんだ。微積という最強手段に頼りすぎて現象をイメージできないのはよくないからね。
とはいえ微積分を使わずにやるのは高校に任せて、このシリーズではガンガン大学数学を使って高校物理をなぞっていくんだ！機械的にできるのってすごいんだよ！
もう高校でやったことはいいんじゃないの？二度手間だし。
なんてことを！
例えば力学の代表的な公式を思い出してほしい。
$$y=\frac{1}{2}gt^2$$$$y=v_0t-\frac{1}{2}gt^2$$$$x=A\sin\omega t$$$$F=mr\omega^2$$$$T=2\pi\sqrt{\frac{l}{g}}$$$$\frac{1}{2}rv\sin\theta=\mathrm{const.}$$
自由落下、鉛直投げ上げ、単振動、向心力、単振り子、面積速度一定だな。
すばらしい。これらの公式はすべてたった１ステップの方法で導かれるんだ。それは
$F=ma$ を解く
これだけなんだ。
確かにそのはずだけど、高校では全部別の単元でばらばらにやったからそういう共通点が見えにくかったかも。落体の運動なんかは運動方程式より前に習うし。面積速度一定は観測結果であるって天下り的に登場したし。
物理を一度ざっと勉強したあとで大切なのは、ワンランク上の原理から既習事項を導出することだと思うんだ。力学の場合、その原理というのがニュートンの運動方程式なんだ。電磁気学の場合はマクスウェル方程式さ。こいつらは微分方程式だから、解くためにはもちろん微積分を使うよ。
物理学はなるべく少ない原理で語るのをよしとするし、それが分かってくると美しさを感じられるんだ。
ニュートンの運動方程式さえ覚えていれば、ほか全部忘れても大丈夫というのが理想なんだな。
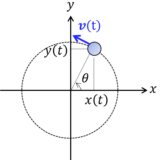
位置ベクトルは $\vec{r}$ とか $\boldsymbol{r}$ と書き、矢印を除くまたはその細字とした $r$ を位置ベクトルの大きさ（原点からの距離）として表します。すなわち $\boldsymbol{r}=(x,y)$ なら$$r=|\boldsymbol{r}|=\sqrt{x^2+y^2}$$です。速さ $v$ は速度ベクトル $\boldsymbol{v}$ の大きさですから$$v= |\boldsymbol{v}|=\sqrt{v^2_x+v^2_y}= \sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}$$こういったさまざまな表現に慣れていくことが大切です。
次の速度ベクトル $\boldsymbol{v}(t)$ , 加速度ベクトル $\boldsymbol{a}(t)$ および速さ $v(t)$ を求めよ．
(1) $\boldsymbol{r}(t)=(t^2,2t)$
(2) $\boldsymbol{r}(t)=(\cos t,\sin t,1)$
(1) $\boldsymbol{v}(t)=(2t,2)$ , $\boldsymbol{a}(t)=(2,0)$ , $v(t)=2\sqrt{t^2+1}$
放物運動の形です。
(2) $\boldsymbol{v}(t)=(-\sin t,\cos t,0)$ , $\boldsymbol{a}(t)=(-\cos t,-\sin t,0)$ , $v(t)=1$
等速円運動です。
（ア）自由落下 $$y(t)=\frac{1}{2}gt^2$$
（イ）鉛直投げ上げ$$y(t)=v_0t-\frac{1}{2}gt^2$$
（ウ）水平投射 $$\boldsymbol{r}(t)=(v_0t,\frac{1}{2}gt^2)$$
これらの加速度の大きさはすべて $g$ であることを確認せよ．
それぞれ２回微分しましょう。
(ア) $a(t)=g$ よりその大きさは $g$
(イ) $a(t)=-g$ よりその大きさは $g$
(ウ) $\boldsymbol{a}(t)=(0,g)$ よりその大きさは $g$
落体の運動の加速度の大きさはすべて $g$ ということは、物体にはたらく力の大きさはすべて $mg$ ということです。
シリーズ一覧
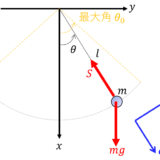
【H7】単振り子の方程式と厳密解
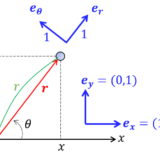
【H6】ベクトルの極座標成分
【H5】等速・非等速円運動と微分方程式
【H4】ばねの微分方程式 水平・鉛直・空気抵抗
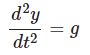
【H3】落体運動の法則はただ１つ
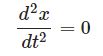
【H2】力がゼロの運動方程式と等速直線運動
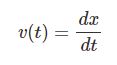
【H1】力学の表現と本シリーズの意義
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
