高校物理の超簡単な実験シリーズ。今回は浮力の測定および物体の密度や体積の計算です。

本シリーズのコンセプトに合わせて、「ざっくり」やれればそれで良いという感じで紹介するよ!
準備物:桶、ばねばかり、密度や体積を知りたい物体(ばねばかりに取り付けるためにタコ糸等がいることも)
※ばねばかりの測定レンジに収まるように物体を選ぶ必要があります。また物体は水より密度の大きいものにします。
※ばねばかりでなく、キッチンスケールでもよいです。その場合は最下部参照。
桶に水を十分にいれておきます。
ここではターゲットの物体として、樹脂製のおもりを使います。フックがついているので、ばねばかりに簡単に吊るせます。
まずはこの物体のおもさを測りましょう。ばねばかりに吊るすと、20g重でした。ニュートン単位に換算するなら、1000で割って0.020kg重とし、9.8をかけます。

次に物体を水に沈めて、ばねばかりの測定値を読みます。すると8g重でした。必要ならばニュートン単位に換算して記録しましょう。

水の密度を $\rho$、物体の密度を $\rho'$ とします。また物体の体積を $V$、重力加速度を $g$ とします。
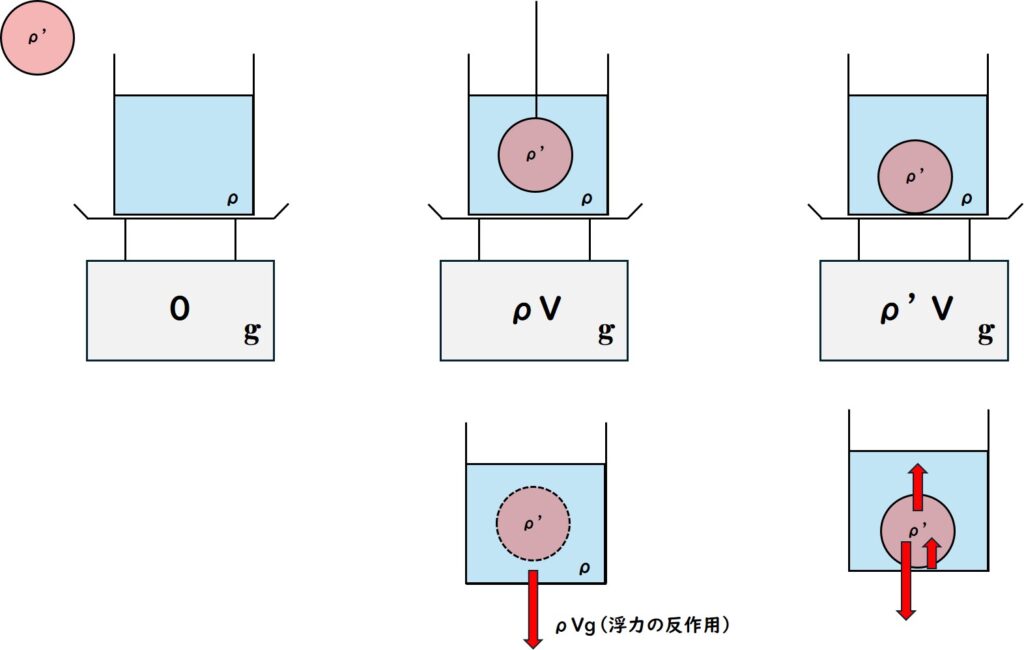
密度kg/m${}^3$、体積m${}^3$、力Nの単位系を選んだ場合、重力は $\rho' Vg$、浮力は $\rho Vg$ となります。本実験では力の単位としてg重を使っていますので、密度をg/cm${}^3$とし、体積をcm${}^3$として重力は $\rho' V$、浮力は $\rho V$ となります。
まず物体のおもさは20g重となりましたので、$$\rho' V=20$$となります(密度の定義そのもの)。
次に水に沈めたときは8g重となりました。ばねばかりが引く力と浮力の和が重力に等しいので$$\rho' V-\rho V=8$$です。水の密度は1g/cm${}^3$ですから$$\rho' V-V=8$$したがって$$V=12\mathrm{cm}^3$$と求まります。なんと物体の体積が求まってしまいました!
1つめの式から$$\rho' =\frac{20}{12}\approx 1.7\mathrm{g/cm}^{3}$$となり、物体の密度まで求まりました!

使用した物体は円柱型だから、ものさしやノギスで直径と高さを計れば、体積を計算できるよ。実験結果と突き合わせることもできるね。

岩石とか、自然界のものの密度を測定するのも面白そう!
キッチンスケールを使う場合、水を入れた容器をスケールにおいてゼロ点とします。おもりを糸でくくって吊るし、水の中に完全に沈めながら浮かせます(底につけちゃだめ)。このときの重量がグラム重単位の浮力となります(浮力の反作用が下向きにはたらくため)。その後おもりを底面に落とします。このときの重量がグラム重単位での重さとなります。後者を前者で割れば密度g/cm3が求まります。
この方法は非常に簡単で良いのですが、なぜこれによって浮力が求まるのかを理解するのが少し難しいです。まず浮かせて測定すると浮力の反作用が現れますが、スケールではグラム重の単位のため、$\rho V$ [g重]となります。さらに水の密度は $\rho=1$ なので、この測定値は結局 $V$ です。つまり物体の体積が求まってしまうのです。物体を底面に落とした場合、スケールにかかる力は「浮力の反作用+物体から受ける力」ですが、「物体から受ける力=スケールが物体に及ぼす抗力」であり、物体のつり合いを考えると「スケールが物体に及ぼす抗力=物体の重量 ー 浮力」。したがってスケールにかかる力は物体の重量と等しく $\rho' V$ [g重]として計測されます。最後に $\rho' V$ を先ほどの測定値 $V$ で割ると $\rho'$ [g/cm3]が現れます。
その他の実験:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。


