【10】開円板上の正則関数とBlaschke積

無限積の理論シリーズ第10回。前回は、与えられた零点を持つ整関数が存在することと、その「因数分解」について考えました。今回は原点中心で任意の半径の開円板上に零点が与えられたとき、それを零点に持つ正則関数がBlaschke積によってつくれることを説明します。このあたりの進め方は、前回と前々回の類似した内容を読んでいただくとスムーズかと思います。

前回はこちら：

【８】整関数とワイエルシュトラスの因数分解定理①（基本乗積・種数）

【９】整関数とワイエルシュトラスの因数分解定理②（完全版）

もくじ [hide]

ブラシュケ積の定義
収束性
より大きな円板を考える場合
例題に挑戦
参考文献

ブラシュケ積の定義

複素平面において、原点中心、半径 $r$ の開円板を $D(0;r)$ 、閉円板を $\bar{D}(0;r)$ と書くことにします。また $\begin{equation}\mathcal{D}:=D(0;1)\;,\quad\bar{\mathcal{D}}:=\bar{D}(0;1)\;,\quad\partial\mathcal{D}:=\bar{\mathcal{D}}\setminus\mathcal{D}\tag{1}\end{equation}$ と定義します。

$a_n\neq 0$ をみたす複素数からなる可算集合 $S=\{a_1,a_2,a_3,\cdots\}$ が $S\subset\mathcal{D}$ であるとします。このとき $S$ に関する $\mathcal{D}$ 上のBlaschke積 $B$ を $\begin{equation}B(z):=e^{i\a}\prod_{n=1}^\infty b_n(z)\;,\quad b_n(z):=\frac{|a_n|}{a_n}\frac{z-a_n}{\bar{a_n}z-1}\tag{2}\end{equation}$ と定義します。 $\mathcal{D}$ 上で定義されていますので、やはり $|z|<1$ であることに注意します。以後、 $\a=0$ とします。

(2)は無限積を含むので、この収束性をのちに確認します。 $b_n$ は $z=a_n$ でゼロとなり、 $B$ の零点を与えます。

また $b_n$ の分母に関して $|\bar{a_n}z-1|\ge 1-|\bar{a_n}||z|> 0$ ですので、極とはなりません。

収束性

(2)の無限積の収束性を調べます。 $\prod_{n=1}^\infty b_n(z)=\prod_{n=1}^\infty (1+c_n(z))\;,\quad c_n(z):=b_n(z)-1$ と書けますので、定理6.8から $\sum |c_n(z)|$ が広義一様収束することと、無限積が広義一様収束することは同値です。このとき無限積は解析関数となります。

定数 $r$ を $|z|\le r<1$ として定めると $\begin{eqnarray*}|c_n(z)| &=& \left|\frac{|a_n|^2z-a_n-|a_n|z+a_n|a_n|}{a_n(\bar{a_n}z-1)}\right| \\&=& \left|\frac{(|a_n|-1)(|a_n|z+a_n)}{a_n(\bar{a_n}z-1)}\right| \\&=& \frac{||a_n|z+a_n|}{|a_n||1-\bar{a_n}z|}(1-|a_n|)\\&\le& \frac{|a_n||z|+|a_n|}{|a_n|(1-|a_n||z|)}(1-|a_n|)\\&\le&\frac{1+r}{1-r^2}(1-|a_n|)\end{eqnarray*}$ $\therefore\quad\sum_{n=1}^\infty|c_n(z)|\le\frac{1}{1-r}\sum_{n=1}^\infty(1-|a_n|)$ よってワイエルシュトラスのM判定法より、 $\bar{D}(0;r)$ では $\begin{equation}\sum_{n=1}^\infty(1-|a_n|)\;\mathrm{:収束}\Longrightarrow\sum_{n=1}^\infty|c_n(z)|\;\mathrm{:一様収束}\tag{3}\end{equation}$ したがって $\mathcal{D}$ 上で $\begin{equation}\sum_{n=1}^\infty(1-|a_n|)\;\mathrm{:収束}\Longrightarrow\sum_{n=1}^\infty|c_n(z)|\;\mathrm{:広義一様収束}\tag{4}\end{equation}$ 定理6.8から $\begin{equation}\sum_{n=1}^\infty(1-|a_n|)\;\mathrm{:収束}\Longrightarrow\prod_{n=1}^\infty b_n(z)\;\mathrm{:広義絶対一様収束}\tag{5}\end{equation}$ と分かります。 $\sum(1-|a_n|)$ が収束する条件をBlaschke conditionといいます。

逆に無限積 $\prod |b_n(z)|$ が $|z|\le r<1$ で一様収束するなら $\sum|c_n(z)|$ も一様収束します。ここで $\begin{eqnarray*}|c_n(z)| &=&\frac{||a_n|z+a_n|}{|a_n||1-\bar{a_n}z|}(1-|a_n|)\\&\ge& \frac{||a_n||z|-|a_n||}{|a_n|(1+|\bar{a_n}||z|)}(1-|a_n|)\\&=&\frac{1-|z|}{(1+|\bar{a_n}||z|)}(1-|a_n|)\\&\ge&\frac{1-r}{(1+r^2)}(1-|a_n|)\end{eqnarray*}$ となることから、 $\sum(1-|a_n|)$ が収束します。したがって $\mathcal{D}$ 上で $\begin{equation}\prod_{n=1}^\infty b_n(z)\;\mathrm{:広義絶対一様収束}\Longrightarrow\sum_{n=1}^\infty(1-|a_n|)\;\mathrm{:収束}\tag{6}\end{equation}$

さて、部分積 $B_n(z):=\prod_{k=1}^n b_k(z)$ は $\mathcal{D}$ 上で解析的かつ $\bar{\mathcal{D}}$ 上で連続です。 $\mathcal{D}$ の境界 $\partial\mathcal{D}$ すなわち $|z|=1$ においては、平易な計算により $|b_k(z)|=1\Longrightarrow |B_n(z)|=1$ が分かります。最大値の原理より $|B_n(z)|$ は $\partial\mathcal{D}$ で最大値をとるので、 $\bar{\mathcal{D}}$ 上、任意の $n$ で $|B_n(z)|\le 1$ を満たします。

アールフォルス[2]を引用すると、最大値の原理とは：

$f(z)$ が有界閉集合 $E$ の上で連続で $E$ の内部では解析的とすると、 $|f(z)|$ は $E$ の境界上で最大値をとる。

以上から、Blaschke積について以下の定理が成立します。

定理10.1

(2)のBlaschke積 $B$ が $|z|<1$ で広義絶対一様収束することと、 $\sum(1-|a_n|)$ が収束すること(Blaschke条件)は同値である。このとき $B$ は $|z|<1$ で正則な関数となり、 $|B(z)|\le 1$ である。

そしてこの $B$ は $\{a_n\}$ を零点にもつ $\mathcal{D}$ 上の有界な正則関数となります。

より大きな円板を考える場合

$D(0;R)$ なる開円板に $\{a_n\}$ が収まっている場合を考えます。先ほどまでの $|z|<1$ で成立した式は、 $|Rz|<R$ で $Rz=w$ とおくと $|w|<R$ となることから、 $B(R,z)=\prod_{n=1}^\infty \frac{|a_n|}{a_n}\frac{R(z-a_n)}{\bar{a_n}z-R^2}$ なる関数がBlaschke積となります。ただし $w$ を $z$ に置きなおしました。この無限積が $D(0;R)$ 上絶対収束することと $\sum(R-|a_n|)$ が収束することは同値になります。なお境界 $|z|=R$ においては $|b_n(z)|=\frac{R|z-a_n|}{|\bar{a_n}z-R^2|}=\frac{R|z-a_n|}{|\bar{a_n}z-z\bar{z}|}=\frac{R}{|z|}\frac{|z-a_n|}{|\overline{z-a_n}|}=1$ よって次のことがいえます。

定理10.2

$D(0;R)$ で定義される（恒等的に $0$ でない）有界な正則関数 $f$ が、 $z=0$ に $m$ 位の零点を、そして $\{a_n\}$ に零点をもつとする。ただし $\{a_n\}$ では零点の位数だけ、重複して同じ数が現れるとする。このとき $\sum(R-|a_n|)$ が収束するならば、 $f$ は $f(z)=g(z)\left(\frac{z}{R}\right)^m\prod_{n=1}^\infty \frac{|a_n|}{a_n}\frac{R(z-a_n)}{\bar{a_n}z-R^2}$ と書ける。ただし $g$ は $D(0;R)$ で定義される、零点をもたない正則関数であり、 $D(0;R)$ で $|f(z)|\le M$ ならば $|g(z)|\le M$ を満たす。

例えば零点を $a_n=R-\frac{1}{n^s}$ とすると、 $s>1$ であれば定理10.2のような $f$ が得られます。ワイエルシュトラスの因数分解定理と主張が類似していることが分かります。異なるのは、考える領域が全平面でないことと、それにともなって零点の列 $\{a_n\}$ が無限集合の場合に発散するのではなく、 $D(0;R)$ の境界で収束することです。

境界 $\partial\mathcal{D}_R$ で収束する場合は可算無限個の零点をもつ。内部で収束する場合は一致の定理より恒等的に0となるため除外。そもそもBlaschke条件 $\sum(R-|a_n|)$ を満たすには $|a_n|\to R$ が必要である。

定理の形としては、分数関数の無限積になっています。

例題に挑戦

例題10.1

$D(0;R)$ 上に零点 $a_n=R-\frac{1}{n^s}$ をもつ正則関数がブラシュケ積の形で書けるような実数 $s$ の範囲を求めよ。

Blaschke条件を満たすようにすればよい。つまり $\sum(R-|a_n|)=\sum\frac{1}{n^{s}}$ が収束すればよいので $s>1$ である。十分大きな $n$ で $a_n>0$ を用いた。

例題10.2

$\cos\frac{1}{2-z}$ のすべての零点を $\{a_n\}$ とする。これは $D(0;2)$ におけるBlaschke条件を満たさないことを示せ。

$a_n=2-\frac{2}{(2n+1)\pi}$ より $\sum(2-|a_n|)$ は発散するため。

次回はこちら：

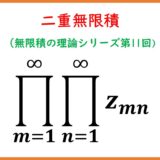2023年8月8日【11】二重無限積

参考文献

今回の記事はほぼ[1]に依拠していますが、ごく簡単に扱われています。。Blaschke積について詳細に知ろうと思ったらマニアックな書籍を読む必要があるのだろうと思います。[3][4]がそれですが、私は読んだことがありません。

[1] Charles H.C.Little, Kee L.Teo, Bruce van Brunt, "An Introduction to Infinite Products" (2022) 楽天はココ。

無限積だけで１冊の本。入門からスタートするので安心です。第1章で級数のおさらいもあります。

[2]アールフォルス. (1982). 複素解析. 現代数学社.

複素解析の超定番本です。

複素解析(Amazon) 複素解析(楽天ブックス) [3] Colwell, P. (1985). Blaschke products: Bounded Analytic Functions.

[4] Mashreghi, J., & Fricain, E. (2012). Blaschke products and their applications. Springer Science & Business Media.

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。