無限積の理論シリーズ第17回。前回導出したヤコビの三重積から得られるいくつかの公式を解説します。オイラーの五角数定理、ガウスの三角数定理、ワトソンの五重積などです。最終回かも。
前回はこちら:
前回示したように、
$|q|<1$ , $z\neq0$ ,$$\prod_{n=0}^\infty(1-q^{2n+2})(1+zq^{2n+1})\left(1+\frac{q^{2n+1}}{z}\right)=\sum_{n=-\infty}^\infty q^{n^2}z^n$$
少し変えた表現として、$z\to qz$ としたものもあります:
$0<|q|<1$ , $z\neq0$ ,$$\prod_{n=1}^\infty(1-q^{2n})(1+zq^{2n})\left(1+\frac{q^{2n-2}}{z}\right)=\sum_{n=-\infty}^\infty q^{n(n+1)}z^n$$
$\mu ,\nu\in\RR$ として、定理16.5で $z\to \pm z^\nu$ , $q\to z^\mu$ , とすれば
$0<|z|<1$ , \begin{eqnarray}\prod_{n=0}^\infty\left(1-z^{2\mu (n+1)}\right)\left(1+z^{\mu(2n+1)+\nu}\right)\left(1+z^{\mu(2n+1)-\nu}\right)&=&\sum_{n=-\infty}^\infty z^{\mu n^2+\nu n}\tag{a}\\\prod_{n=0}^\infty\left(1-z^{2\mu (n+1)}\right)\left(1-z^{\mu(2n+1)+\nu}\right)\left(1-z^{\mu(2n+1)-\nu}\right)&=&\sum_{n=-\infty}^\infty (-1)^nz^{\mu n^2+\nu n}\tag{b}\end{eqnarray}
定理の導出
系17.2(b)で $\mu=3/2$ , $\nu=1/2$ を代入すると$$\prod_{n=1}^\infty(1-z^{3n})(1-z^{3n-1})(1-z^{3n-2})=\sum_{n=-\infty}^\infty(-1)^nz^{\frac{n(3n+1)}{2}}$$左辺は3で割った余りごとの積になっています。結局、\begin{equation}\prod_{n=1}^\infty(1-z^{n})=\sum_{n=-\infty}^\infty(-1)^nz^{\frac{n(3n+1)}{2}}\tag{1}\end{equation}(1)は公式としての体を成していますが、あえて右辺で $n\to -n$ としてオイラーの五角数定理とよびます。
$0<|z|<1$ ,$$\prod_{n=1}^\infty(1-z^{n})=\sum_{n=-\infty}^\infty(-1)^nz^{\frac{n(3n-1)}{2}}$$
右辺に五角数:\begin{equation}g(n):=\frac{n(3n-1)}{2}\tag{2}\end{equation}を用いています。次のように五角形を繰り返し重ねていくと、点の数が $1,5,12,\cdots$ すなわち $g(n)$ となります。
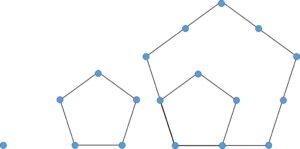
定理17.3をqポッホハマー記号で表すなら、$z$ を $q$ に書き換えて\begin{equation}(q;q)_\infty=\sum_{n=-\infty}^\infty(-1)^nq^{\frac{n(3n-1)}{2}}\tag{3}\end{equation}です。
分割の話
(1)の右辺を $n$ が正、0、負で分けて書くと\begin{equation}\prod_{n=1}^\infty(1-z^{n})=1+\sum_{n=1}^\infty(-1)^n\left\{z^{g(n)}+z^{g(-n)}\right\}\tag{4}\end{equation}
定理15.3より\begin{equation}\prod_{n=1}^\infty (1-z^{n})=1+\sum_{n=1}^\infty \{A^*_e(n)-A^*_o(n)\}z^n\tag{5}\end{equation}右辺の無限和のなかにある $n$ 次の係数は、$n$ を自然数によって異分割するときの、「偶数個の成分をもつ場合の数」を$A^*_e(n)$、「奇数個の成分をもつ場合の数」を $A^*_o(n)$ と表しています。
(4)(5)を見比べると、$n=\frac{k(3k\pm 1)}{2}$ のときは $A^*_e(n)-A^*_o(n)=(-1)^k$ であり、それ以外では $A^*_e(n)=A^*_o(n)$ となります。$n=\frac{k(3k\pm 1)}{2}$ を書き出すと $n=1,2$,$5,7$,$12,15$,$\cdots$ です。実際に異分割(distinct partition)を書き出してみると確かにそうなっています。\begin{array}{c|lccc}n&\mathrm{distinct\:partition}&A^*_e(n)&A^*_o(n)&A^*_e(n)-A^*_o(n) \\\hline 1&[1]&0&1&-1\\2&[2]&0&1&-1\\3&[1,2][3]&1&1&0\\4&[1,3][4]&1&1&0\\5&[1,4][2,3][5]&2&1&1\\6&[1,5][2,4][1,2,3][6]&2&2&0\\7&[1,6][2,5][3,4][1,2,4][7]&3&2&1\\8&[1,7][2,6][3,5][1,2,5][1,3,4][8]&3&3&0\end{array}
系17.2(a)で $\mu=\nu=1/2$ とすると\begin{eqnarray*}&&\prod_{n=0}^\infty(1-z^{n+1})(1+z^{n+1})(1+z^n)=\sum_{n=-\infty}^\infty z^\frac{n(n+1)}{2}\\&&\Rightarrow \prod_{n=1}^\infty(1-z^{2n})\prod_{n=1}^\infty(1+z^n)=\frac{1}{2}\sum_{n=-\infty}^\infty z^\frac{n(n+1)}{2}\end{eqnarray*}オイラーの分割恒等式より$$\prod_{n=1}^\infty\frac{1-z^{2n}}{1-z^{2n-1}}=\frac{1}{2}\sum_{n=-\infty}^\infty z^\frac{n(n+1)}{2}$$右辺は$$\sum_{n=-\infty}^\infty z^\frac{n(n+1)}{2}=\sum_{n=0}^\infty z^\frac{n(n+1)}{2}+\sum_{n=1}^{\infty} z^\frac{n(n-1)}{2}=2\sum_{n=0}^\infty z^\frac{n(n+1)}{2}$$によりガウスの三角数定理を得ます。
$$\prod_{n=1}^\infty\frac{1-z^{2n}}{1-z^{2n-1}}=\sum_{n=0}^\infty z^\frac{n(n+1)}{2}$$
定理16.5で $z\to -qz$ とすると$$\prod_{n=0}^\infty(1-q^{2n+2})(1-zq^{2n+2})\left(1-\frac{q^{2n}}{z}\right)=\sum_{n=-\infty}^\infty (-1)^nq^{n(n+1)}z^n$$両辺を少し変形すると$$(1-z^{-1})\prod_{n=1}^\infty(1-q^{2n})(1-zq^{2n})\left(1-\frac{q^{2n}}{z}\right)=\sum_{n=0}^\infty (-1)^nq^{n(n+1)}z^n+\sum_{n=1}^\infty (-1)^nq^{n(n-1)}z^{-n}$$右辺の2つめの和の添え字を1つずらして$$(1-z^{-1})\prod_{n=1}^\infty(1-q^{2n})(1-zq^{2n})\left(1-\frac{q^{2n}}{z}\right)=\sum_{n=0}^\infty (-1)^nq^{n(n+1)}\{z^n-z^{-n-1}\}$$よって\begin{eqnarray*}\prod_{n=1}^\infty(1-q^{2n})(1-zq^{2n})\left(1-\frac{q^{2n}}{z}\right)&=&\sum_{n=0}^\infty (-1)^nq^{n(n+1)}z^n\frac{1-z^{-2n-1}}{1-z^{-1}}\\ &=&\sum_{n=0}^\infty (-1)^nq^{n(n+1)}z^n(1+z^{-1}+\cdots+z^{-2n})\end{eqnarray*}$z\to 1$ として
$|z|<1$,$$\prod_{n=1}^\infty (1-z^n)^3=\sum_{n=0}^\infty (-1)^n(2n+1)z^\frac{n(n+1)}{2}$$
系17.1で $z\to -z$ とすると\begin{equation}\prod_{n=1}^\infty(1-q^{2n})(1-zq^{2n})\left(1-\frac{q^{2n-2}}{z}\right)=\sum_{n=-\infty}^\infty (-1)^nq^{n(n+1)}z^n\tag{6}\end{equation}定理16.5で $q\to q^2$ , $z\to -z^2$ として\begin{equation}\prod_{n=1}^\infty(1-q^{4n})(1-z^2q^{4n-2})\left(1-\frac{q^{4n-2}}{z^2}\right)=\sum_{n=-\infty}^\infty (-1)^nq^{2n^2}z^{2n}\tag{7}\end{equation}定理17.3で $z\to q^4$ として\begin{equation}\prod_{n=1}^\infty(1-q^{4n})=\sum_{n=-\infty}^\infty(-1)^nq^{2n(3n-1)}\tag{8}\end{equation}(6)(7)(8)はあとで用います。
さて、ここで\begin{eqnarray*}&&\sum_{m=-\infty}^\infty(-1)^mq^{2m(3m-1)}\sum_{n=-\infty}^\infty q^{n(3n+1)}(z^{3n}-z^{-3n-1})\\&=& \sum_{m=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^mq^{2m(3m-1)+n(3n+1)}(z^{3n}-z^{-3n-1})\\&=&\sum_{m=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^mq^{2m(3m-1)+n(3n+1)}z^{3n}-\sum_{m=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^mq^{2m(3m-1)+n(3n+1)}z^{-3n-1} \end{eqnarray*}右辺の2つめの和で $m\to -m$ , $n\to -n$ として\begin{eqnarray*}&=& \sum_{m=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^mq^{2m(3m-1)+n(3n+1)}z^{3n}-\sum_{m=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^mq^{2m(3m+1)+n(3n-1)}z^{3n-1}\end{eqnarray*}$m\to k-n$ として\begin{eqnarray*}&=& \sum_{k=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^{k-n}q^{(3n-2k)(3n-2k+1)+2k^2}z^{3n}-\sum_{k=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^{k-n}q^{(3n-1-2k)(3n-2k)+2k^2}z^{3n-1}\\&=&\sum_{k=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^{3n-k}q^{(3n-2k)(3n-2k+1)+2k^2}z^{3n}+\sum_{k=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^{3n-1-k}q^{(3n-1-2k)(3n-1-2k+1)+2k^2}z^{3n-1}\end{eqnarray*}1つ目の和は $3n$ 、2つ目の和は $3n-1$ になっています。ここで $3n-2$ については\begin{eqnarray*}&&\sum_{k=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^{3n-2-k}q^{(3n-2-2k)(3n-2-2k+1)+2k^2}z^{3n-2}\\&=&\sum_{m=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^{m+2n-2}q^{3n^2-3n+6m^2-6m+2}z^{3n-2}\quad(k\to n-m)\\&=&\sum_{m=-\infty}^\infty(-1)^m(q^6)^{m(m-1)}\sum_{n=-\infty}^\infty q^{3n^2-3n+2}z^{3n-2}\\&=&\left(\sum_{m=1}^\infty(-1)^m(q^6)^{m(m-1)}+\sum_{m=0}^\infty(-1)^m(q^6)^{m(m+1)}\right)\sum_{n=-\infty}^\infty q^{3n^2-3n+2}z^{3n-2}\\&=&0\end{eqnarray*}となるので結局$$\sum_{m=-\infty}^\infty(-1)^mq^{2m(3m-1)}\sum_{n=-\infty}^\infty q^{n(3n+1)}(z^{3n}-z^{-3n-1})=\sum_{k=-\infty}^\infty\sum_{n=-\infty}^\infty(-1)^{n-k}q^{(n-2k)(n-2k+1)+2k^2}z^{n}$$$n\to j+2k$ とすれば$$=\sum_{k=-\infty}^\infty\sum_{j=-\infty}^\infty(-1)^{j+k}q^{j(j+1)+2k^2}z^{j+2k}$$$$\therefore\quad\sum_{m=-\infty}^\infty(-1)^mq^{2m(3m-1)}\sum_{n=-\infty}^\infty q^{n(3n+1)}(z^{3n}-z^{-3n-1})=\sum_{k=-\infty}^\infty(-1)^kq^{2k^2}z^{2k}\sum_{j=-\infty}^\infty(-1)^{j}q^{j(j+1)}z^{j}$$左辺には(8)を、右辺には(6)(7)を用いることで、$$\sum_{n=-\infty}^\infty q^{n(3n+1)}(z^{3n}-z^{-3n-1})=\prod_{n=1}^\infty(1-q^{2n})(1-zq^{2n})\left(1-\frac{q^{2n-2}}{z}\right)(1-z^2q^{4n-2})\left(1-\frac{q^{4n-2}}{z^2}\right)$$ただし $0<|q|<1$ , $0<|z|<1$ です。これはもう少し広い範囲で成り立ち、次のワトソンの五重積を得ます。
$0<|q|<1$ , $z\neq 0$ ,$$\sum_{n=-\infty}^\infty q^{n(3n+1)}(z^{3n}-z^{-3n-1})=\prod_{n=1}^\infty(1-q^{2n})(1-zq^{2n})\left(1-\frac{q^{2n-2}}{z}\right)(1-z^2q^{4n-2})\left(1-\frac{q^{4n-2}}{z^2}\right)$$
$|z|<1$ のとき\begin{eqnarray*}\prod_{n=0}^\infty(1-z^{2n+2})(1-z^{2n+1})^2&=&\sum_{n=-\infty}^\infty(-1)^nz^{n^2}\\\prod_{n=0}^\infty(1-z^{2n+2})(1+z^{2n+1})^2&=&\sum_{n=-\infty}^\infty z^{n^2}\end{eqnarray*}を示せ。
定理16.5で $z\to1$ , $q\to \pm z$ として得る。
$0<|z|<1$ のとき\begin{eqnarray*}\prod_{n=0}^\infty(1-z^{5n+5})(1-z^{5n+4})(1-z^{5n+1})&=&\sum_{n=-\infty}^\infty(-1)^nz^{\frac{n(5n+3)}{2}}\\\prod_{n=0}^\infty(1-z^{5n+5})(1-z^{5n+3})(1-z^{5n+2})&=&\sum_{n=-\infty}^\infty(-1)^nz^{\frac{n(5n+1)}{2}}\end{eqnarray*}を示せ。
系17.2(b)で $\mu=5/2$ , $\nu=3/2$ および $\mu=5/2$ , $\nu=1/2$ として得る。
無限積の理論シリーズはこれでおしまい!第1回はこちら:
無限積だけで1冊の本。入門からスタートするので安心です。第1章で級数のおさらいもあります。

数論の入門として名高い本。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。

