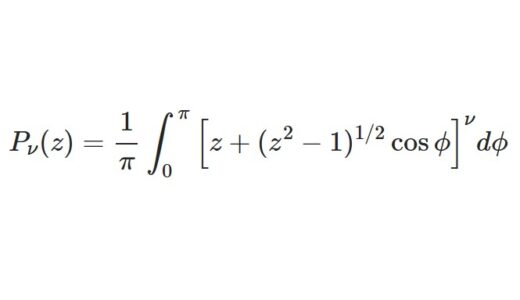前回はこちら:
第1種ルジャンドル関数 $P_\nu(z)$ は、$\nu$ が整数のとき(今回は特に非負整数のとき)にルジャンドル多項式とよばれるのでした。本シリーズの第1回で解説しています。
ルジャンドル多項式はその名の通り多項式で表現されるものであり、$P_n(z)$ は $z$ の $n$ 次式なのでした。\begin{align}P_0(z) &= 1\\P_1(z)&=z\\ P_2(z) &=\frac{3z^2-1}{2}\\ P_3(z) &=\frac{5z^3-3z}{2}\end{align}今回は、逆に任意の多項式をルジャンドル多項式の線形結合で書けないか?すなわち多項式 $f(z)$ に対して$$f(z)=a_0P_0(z)+a_1P_1(z)+\cdots+a_nP_n$$のように表せないか、というテーマで話を進めます。
上で書いた式を使うと、2次以下の多項式$$f_2(z)=b_0+b_1z+b_2z^2$$は $P_0,P_1,P_2$ を用いて次のように書けます。$$f_2(z)=\left(b_0+\frac{b_2}{3}\right)P_0(z)+b_1P_1(z)+\frac{2}{3}b_2P_2(z)$$このように $n$ 次の多項式は $P_0$ から $P_n$ を用いて書けそうです。
ただ任意の多項式では少々面倒です。そこでシンプルな多項式 $z^n$ を $P_0,\cdots,P_n$ で表す方法を考えましょう。例えば$$z^5=\frac{3}{7}P_1(z)+\frac{4}{9}P_3(z)+\frac{8}{63}P_5(z)$$のようにです。そうすれば結果的に任意の多項式をルジャンドル多項式で表せるということになります。
最高次から調べる
第1回の定理1を再掲します。
$n$ 次のルジャンドル多項式 $P_n(z)$ は次の形で明示される。$$P_n(z)=\sum_{m=0}^{\lfloor \frac{n}{2}\rfloor}\frac{(2n-2m)!}{2^nm!(n-m)!(n-2m)!}z^{n-2m}$$
これによれば $P_n$ の最高次($z^n$)の係数は$$\frac{(2n)!}{2^n(n!)^2}$$です。
さて多項式 $z^n$ は \begin{equation}z^n=a_0P_0+a_1P_1+\cdots+a_{n-1}P_{n-1}+a_nP_n\tag{1}\end{equation}と表現できます。(1)の右辺は当然 $z$ の $n$ 次式ですが、その $n$ 次の項は $P_n$ だけがもっています。なので $P_n$ の最高次係数と比較して\begin{equation}a_n=\frac{2^n(n!)^2}{(2n)!}\tag{2}\end{equation}だと分かります。
直交性の利用
ルジャンドル多項式の重要な性質である直交性についておさらいします。
$$\int_{-1}^1 P_m(z)P_n(z)dz=\begin{cases}0\quad &(m\neq n)\\\cfrac{2}{2n+1}\quad &(m=n)\end{cases}$$
定理2をおさえたうえで、次の積分を定義します。\begin{equation}I_{m,n} :=\int_{-1}^1 z^m P_n(z)dz\tag{3}\end{equation}(1)を使うと\begin{equation}I_{m,n} = \sum_{k=0}^ma_k\int_{-1}^1 P_k(z)P_n(z)dz\tag{4}\end{equation}
もし $m<n$ だと定理2により $I_{m,n}=0$ となります。
また定理1から $P_n$ の偶奇性が分かり、$m-n$ が奇数の場合は $z^mP_n(z)$ は奇関数だと判明します。以上から次の事実がとりあえず分かります。
$m<n$ の場合、あるいは $m-n$ が奇数の場合 $I_{m,n}=0$ .
次に $m=n$ の場合は(4)と定理2より$$I_{m,m}=a_m\frac{2}{2m+1}$$(2)より $a_m=\dfrac{2^m(m!)^2}{(2m)!}$ なので
\begin{equation}I_{m,m} = \frac{2^{m+1}(m!)^2}{(2m+1)!}\tag{5}\end{equation}
微分方程式の利用
次に本丸ともいえる $m>n$ の場合を考えます。上の議論から、もちろん $m-n$ を偶数に限ればよいです。
ルジャンドル関数が満たす微分方程式$$\frac{d}{dz}\left((1-z^2)\frac{dy}{dz}\right)+n(n+1)y=0$$を(3)に用いると$$I_{m,n}=\frac{1}{n(n+1)}\int_{-1}^1 z^m\frac{d}{dz}\left((z^2-1)P'_n(z)\right)dz$$部分積分をすると$$I_{m,n}=\frac{1}{n(n+1)}\left[m(m+1)\int_{-1}^1z^mP_n(z)dz-m(m-1)\int_{-1}^1z^{m-2}P_n(z)dz\right]$$$I_{m,n}$ の定義から右辺を書き直して\begin{equation}I_{m,n}=\frac{1}{n(n+1)}\left[m(m+1)I_{m,n}-m(m-1)I_{m-2,n}\right]\tag{6}\end{equation}\begin{equation}\therefore\quad I_{m,n}=\frac{m(m-1)}{(m-n)(m+n+1)}I_{m-2,n}\tag{7}\end{equation}この漸化式を繰り返し用います。$m-n$ が偶数であることから最終的に $I_{n,n}$ が現れ、(5)を使えばよいです。最終的に
$m>n$ , $m-n:\textrm{even}$,\begin{equation}I_{m,n} =\frac{2^{n+1}m!(\frac{m+n}{2})!}{(m+n+1)!(\frac{m-n}{2})!}\tag{8}\end{equation}
以上から$$z^m=a_0P_0(z)+a_1P_1(z)+\cdots+a_{m-1}P_{m-1}(z)+a_mP_m(z)$$においてルジャンドル多項式の直交性から$$a_n=\frac{2n+1}{2}I_{m,n}$$であることより次の結論が導かれます。
$$z^m=a_0P_0(z)+a_1P_1(z)+\cdots+a_{m-1}P_{m-1}(z)+a_mP_m(z)$$における係数 $a_n$ は$$a_n=\left\{\begin{array}{cl}0 &(m<n\;\lor\; m-n:\mathrm{odd})\\\dfrac{2^{n}(2n+1)m!(\frac{m+n}{2})!}{(m+n+1)!(\frac{m-n}{2})!} &(m\ge n\;\land\; m-n:\mathrm{even})\end{array}\right.$$
定理3を使って $z^5$ を表せ。
$a_0,\cdots ,a_5$ を計算すればよい。$$a_n=\left\{\begin{array}{cl}0 &(n=0,2,4)\\\dfrac{2^{n}(2n+1)\cdot 120\cdot(\frac{n+5}{2})!}{(n+6)!(\frac{5-n}{2})!} &(n=1,3,5)\end{array}\right.$$最終的に$$z^5=\frac{3}{7}P_1(z)+\frac{4}{9}P_3(z)+\frac{8}{63}P_5(z)$$
$$\int_{-1}^1 z P_n(z)P_{n+1}(z)dz$$を計算せよ。
$zP_n$ は $z$ の $n+1$ 次式であるから$$zP_n=a_0P_0+a_1P_1+\cdots +a_{n+1}P_{n+1}$$とおける。$z^{n+1}$ の係数を比較して$$\frac{(2n)!}{2^nn!^2}=a_{n+1}\frac{(2n+2)!}{2^{n+1}(n+1)!^2}$$$$\therefore\quad a_n=\frac{n+1}{2n+1}$$したがって直交性を利用すれば$$\int_{-1}^1 z P_n(z)P_{n+1}(z)dz=\frac{2n+2}{(2n+1)(2n+3)}$$
この結論により例えば$$\int_{-1}^1 z P_{499}(z)P_{500}(z)dz=\frac{1000}{999999}$$と魔法のように計算できます。
ちなみに少し違う積分は$$\int_{-1}^1 z^2 P_n(z)P_{n+1}(z)dz=0$$これも簡単なので確認してみてください。
$$\int_{-1}^1 z^3 P_n(z)P_{n+3}(z)dz$$を計算せよ。
問題2と同様。$z^{n+3}$ で係数比較する。答えは$$\int_{-1}^1 z^3 P_n(z)P_{n+3}(z)dz=\frac{2(n+1)(n+2)(n+3)}{(2n+1)(2n+3)(2n+5)(2n+7)}$$
$$\int_{-1}^1 z^3 P_n(z)P_{n+1}(z)dz=\frac{6(n+1)(n^2+2n-1)}{(2n-1)(2n+1)(2n+3)(2n+5)}$$
第5版です。いわずと知れた名著。特殊関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。